Road Graph Generator: Mapping roads at construction sites from GPS data

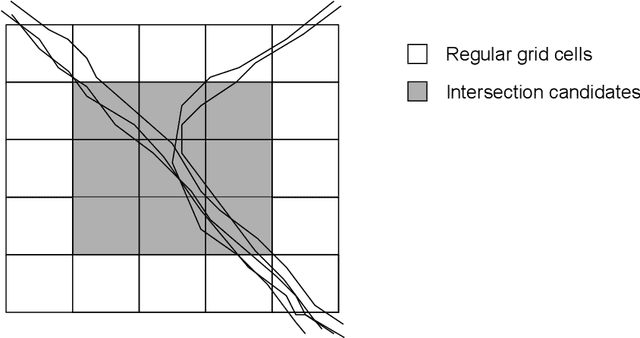
We present a method for road inference from GPS trajectories to map construction sites. This task introduces a unique challenge due to the erratic and non-standard movement patterns of construction machinery, which diverge significantly from typical vehicular traffic on established roads. Our method first identifies intersections in the road network that serve as critical decision points, and later connects them with edges, producing a graph, which subsequently can be used for planning and task-allocation. We demonstrate the effectiveness of our approach by mapping roads at a real-life construction site in Norway.

DON-LSTM: Multi-Resolution Learning with DeepONets and Long Short-Term Memory Neural Networks

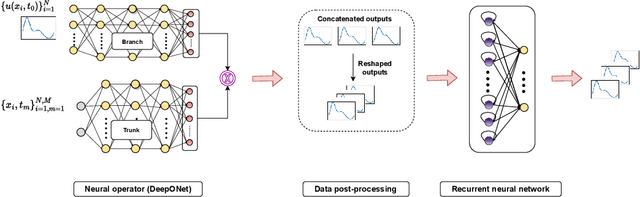
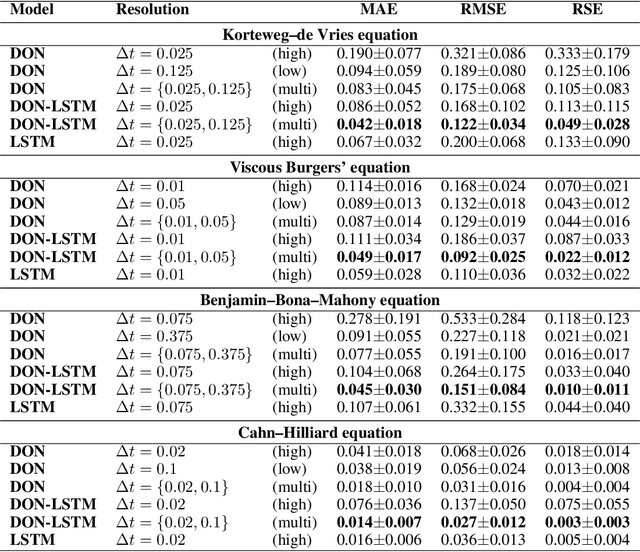
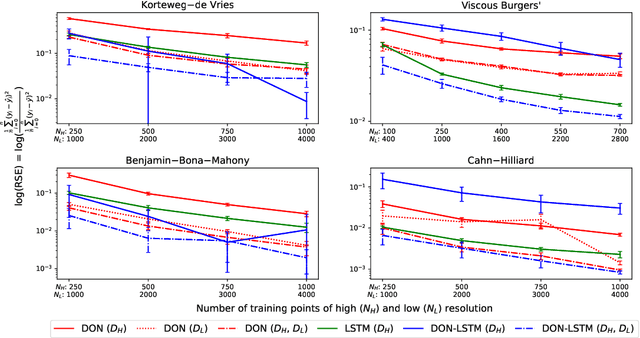
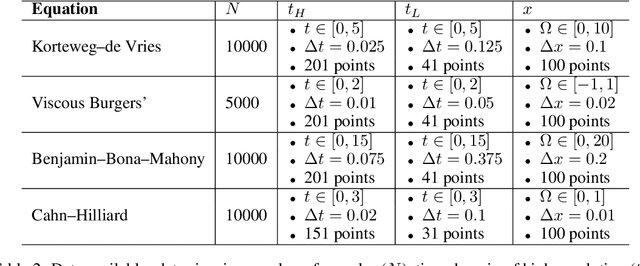
Deep operator networks (DeepONets, DONs) offer a distinct advantage over traditional neural networks in their ability to be trained on multi-resolution data. This property becomes especially relevant in real-world scenarios where high-resolution measurements are difficult to obtain, while low-resolution data is more readily available. Nevertheless, DeepONets alone often struggle to capture and maintain dependencies over long sequences compared to other state-of-the-art algorithms. We propose a novel architecture, named DON-LSTM, which extends the DeepONet with a long short-term memory network (LSTM). Combining these two architectures, we equip the network with explicit mechanisms to leverage multi-resolution data, as well as capture temporal dependencies in long sequences. We test our method on long-time-evolution modeling of multiple non-linear systems and show that the proposed multi-resolution DON-LSTM achieves significantly lower generalization error and requires fewer high-resolution samples compared to its vanilla counterparts.

Neural Operator Learning for Long-Time Integration in Dynamical Systems with Recurrent Neural Networks

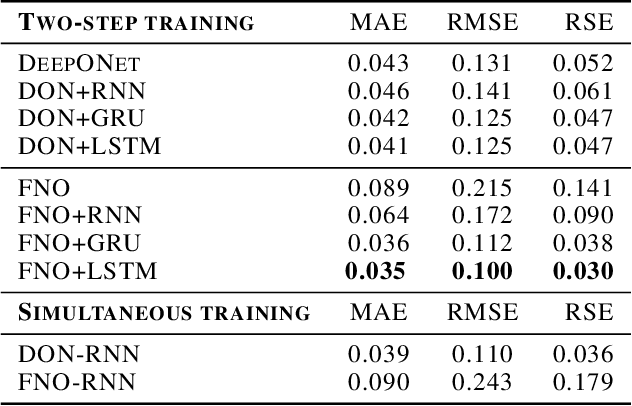
Deep neural networks are an attractive alternative for simulating complex dynamical systems, as in comparison to traditional scientific computing methods, they offer reduced computational costs during inference and can be trained directly from observational data. Existing methods, however, cannot extrapolate accurately and are prone to error accumulation in long-time integration. Herein, we address this issue by combining neural operators with recurrent neural networks to construct a novel and effective architecture, resulting in superior accuracy compared to the state-of-the-art. The new hybrid model is based on operator learning while offering a recurrent structure to capture temporal dependencies. The integrated framework is shown to stabilize the solution and reduce error accumulation for both interpolation and extrapolation of the Korteweg-de Vries equation.