Recency-Weighted Temporally-Segmented Ensemble for Time-Series Modeling

Time-series modeling in process industries faces the challenge of dealing with complex, multi-faceted, and evolving data characteristics. Conventional single model approaches often struggle to capture the interplay of diverse dynamics, resulting in suboptimal forecasts. Addressing this, we introduce the Recency-Weighted Temporally-Segmented (ReWTS, pronounced `roots') ensemble model, a novel chunk-based approach for multi-step forecasting. The key characteristics of the ReWTS model are twofold: 1) It facilitates specialization of models into different dynamics by segmenting the training data into `chunks' of data and training one model per chunk. 2) During inference, an optimization procedure assesses each model on the recent past and selects the active models, such that the appropriate mixture of previously learned dynamics can be recalled to forecast the future. This method not only captures the nuances of each period, but also adapts more effectively to changes over time compared to conventional `global' models trained on all data in one go. We present a comparative analysis, utilizing two years of data from a wastewater treatment plant and a drinking water treatment plant in Norway, demonstrating the ReWTS ensemble's superiority. It consistently outperforms the global model in terms of mean squared forecasting error across various model architectures by 10-70\% on both datasets, notably exhibiting greater resilience to outliers. This approach shows promise in developing automatic, adaptable forecasting models for decision-making and control systems in process industries and other complex systems.

Learning Dynamical Systems from Noisy Data with Inverse-Explicit Integrators

We introduce the mean inverse integrator (MII), a novel approach to increase the accuracy when training neural networks to approximate vector fields of dynamical systems from noisy data. This method can be used to average multiple trajectories obtained by numerical integrators such as Runge-Kutta methods. We show that the class of mono-implicit Runge-Kutta methods (MIRK) has particular advantages when used in connection with MII. When training vector field approximations, explicit expressions for the loss functions are obtained when inserting the training data in the MIRK formulae, unlocking symmetric and high-order integrators that would otherwise be implicit for initial value problems. The combined approach of applying MIRK within MII yields a significantly lower error compared to the plain use of the numerical integrator without averaging the trajectories. This is demonstrated with experiments using data from several (chaotic) Hamiltonian systems. Additionally, we perform a sensitivity analysis of the loss functions under normally distributed perturbations, supporting the favorable performance of MII.

Pseudo-Hamiltonian system identification

Identifying the underlying dynamics of physical systems can be challenging when only provided with observational data. In this work, we consider systems that can be modelled as first-order ordinary differential equations. By assuming a certain pseudo-Hamiltonian formulation, we are able to learn the analytic terms of internal dynamics even if the model is trained on data where the system is affected by unknown damping and external disturbances. In cases where it is difficult to find analytic terms for the disturbances, a hybrid model that uses a neural network to learn these can still accurately identify the dynamics of the system as if under ideal conditions. This makes the models applicable in situations where other system identification models fail. Furthermore, we propose to use a fourth-order symmetric integration scheme in the loss function and avoid actual integration in the training, and demonstrate on varied examples how this leads to increased performance on noisy data.

Pseudo-Hamiltonian neural networks for learning partial differential equations

Pseudo-Hamiltonian neural networks (PHNN) were recently introduced for learning dynamical systems that can be modelled by ordinary differential equations. In this paper, we extend the method to partial differential equations. The resulting model is comprised of up to three neural networks, modelling terms representing conservation, dissipation and external forces, and discrete convolution operators that can either be learned or be prior knowledge. We demonstrate numerically the superior performance of PHNN compared to a baseline model that models the full dynamics by a single neural network. Moreover, since the PHNN model consists of three parts with different physical interpretations, these can be studied separately to gain insight into the system, and the learned model is applicable also if external forces are removed or changed.

Port-Hamiltonian Neural Networks with State Dependent Ports

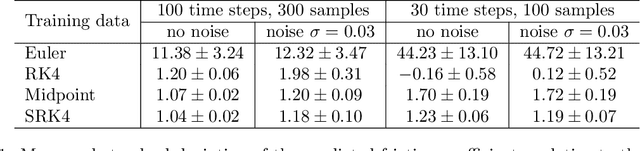
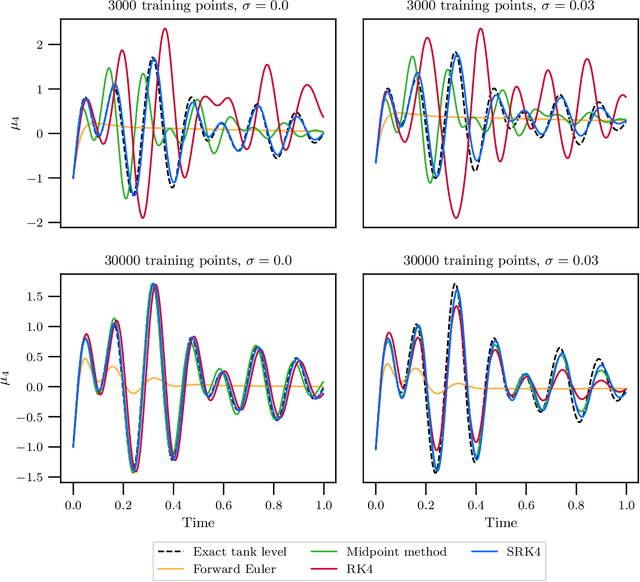
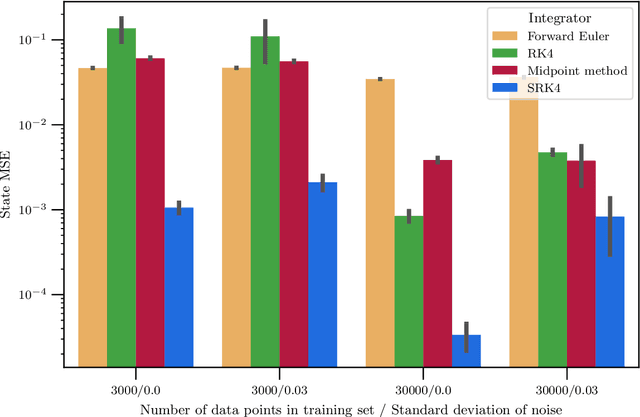
Hybrid machine learning based on Hamiltonian formulations has recently been successfully demonstrated for simple mechanical systems. In this work, we stress-test the method on both simple mass-spring systems and more complex and realistic systems with several internal and external forces, including a system with multiple connected tanks. We quantify performance under various conditions and show that imposing different assumptions greatly affect the performance during training presenting advantages and limitations of the method. We demonstrate that port-Hamiltonian neural networks can be extended to larger dimensions with state-dependent ports. We consider learning on systems with known and unknown external forces and show how it can be used to detect deviations in a system and still provide a valid model when the deviations are removed. Finally, we propose a symmetric high-order integrator for improved training on sparse and noisy data.