Approximation properties of neural ODEs

We study the approximation properties of shallow neural networks whose activation function is defined as the flow of a neural ordinary differential equation (neural ODE) at the final time of the integration interval. We prove the universal approximation property (UAP) of such shallow neural networks in the space of continuous functions. Furthermore, we investigate the approximation properties of shallow neural networks whose parameters are required to satisfy some constraints. In particular, we constrain the Lipschitz constant of the flow of the neural ODE to increase the stability of the shallow neural network, and we restrict the norm of the weight matrices of the linear layers to one to make sure that the restricted expansivity of the flow is not compensated by the increased expansivity of the linear layers. For this setting, we prove approximation bounds that tell us the accuracy to which we can approximate a continuous function with a shallow neural network with such constraints. We prove that the UAP holds if we consider only the constraint on the Lipschitz constant of the flow or the unit norm constraint on the weight matrices of the linear layers.

Designing Stable Neural Networks using Convex Analysis and ODEs

Motivated by classical work on the numerical integration of ordinary differential equations we present a ResNet-styled neural network architecture that encodes non-expansive (1-Lipschitz) operators, as long as the spectral norms of the weights are appropriately constrained. This is to be contrasted with the ordinary ResNet architecture which, even if the spectral norms of the weights are constrained, has a Lipschitz constant that, in the worst case, grows exponentially with the depth of the network. Further analysis of the proposed architecture shows that the spectral norms of the weights can be further constrained to ensure that the network is an averaged operator, making it a natural candidate for a learned denoiser in Plug-and-Play algorithms. Using a novel adaptive way of enforcing the spectral norm constraints, we show that, even with these constraints, it is possible to train performant networks. The proposed architecture is applied to the problem of adversarially robust image classification, to image denoising, and finally to the inverse problem of deblurring.

Learning Dynamical Systems from Noisy Data with Inverse-Explicit Integrators

We introduce the mean inverse integrator (MII), a novel approach to increase the accuracy when training neural networks to approximate vector fields of dynamical systems from noisy data. This method can be used to average multiple trajectories obtained by numerical integrators such as Runge-Kutta methods. We show that the class of mono-implicit Runge-Kutta methods (MIRK) has particular advantages when used in connection with MII. When training vector field approximations, explicit expressions for the loss functions are obtained when inserting the training data in the MIRK formulae, unlocking symmetric and high-order integrators that would otherwise be implicit for initial value problems. The combined approach of applying MIRK within MII yields a significantly lower error compared to the plain use of the numerical integrator without averaging the trajectories. This is demonstrated with experiments using data from several (chaotic) Hamiltonian systems. Additionally, we perform a sensitivity analysis of the loss functions under normally distributed perturbations, supporting the favorable performance of MII.

Predictions Based on Pixel Data: Insights from PDEs and Finite Differences

Neural networks are the state-of-the-art for many approximation tasks in high-dimensional spaces, as supported by an abundance of experimental evidence. However, we still need a solid theoretical understanding of what they can approximate and, more importantly, at what cost and accuracy. One network architecture of practical use, especially for approximation tasks involving images, is convolutional (residual) networks. However, due to the locality of the linear operators involved in these networks, their analysis is more complicated than for generic fully connected neural networks. This paper focuses on sequence approximation tasks, where a matrix or a higher-order tensor represents each observation. We show that when approximating sequences arising from space-time discretisations of PDEs we may use relatively small networks. We constructively derive these results by exploiting connections between discrete convolution and finite difference operators. Throughout, we design our network architecture to, while having guarantees, be similar to those typically adopted in practice for sequence approximation tasks. Our theoretical results are supported by numerical experiments which simulate linear advection, the heat equation, and the Fisher equation. The implementation used is available at the repository associated to the paper.

Dynamical systems' based neural networks

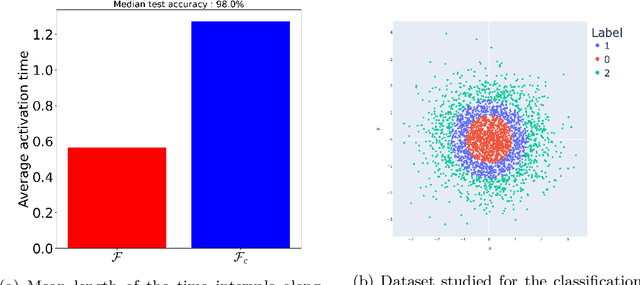
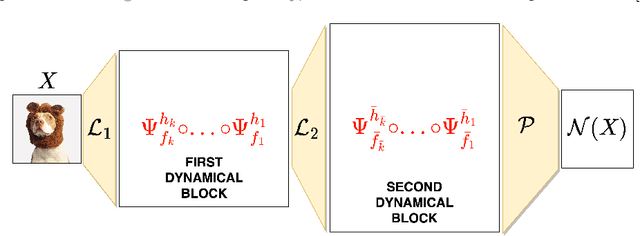
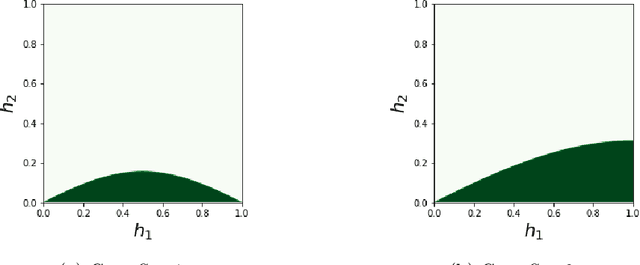
Neural networks have gained much interest because of their effectiveness in many applications. However, their mathematical properties are generally not well understood. If there is some underlying geometric structure inherent to the data or to the function to approximate, it is often desirable to take this into account in the design of the neural network. In this work, we start with a non-autonomous ODE and build neural networks using a suitable, structure-preserving, numerical time-discretisation. The structure of the neural network is then inferred from the properties of the ODE vector field. Besides injecting more structure into the network architectures, this modelling procedure allows a better theoretical understanding of their behaviour. We present two universal approximation results and demonstrate how to impose some particular properties on the neural networks. A particular focus is on 1-Lipschitz architectures including layers that are not 1-Lipschitz. These networks are expressive and robust against adversarial attacks, as shown for the CIFAR-10 dataset.

Deep learning of diffeomorphisms for optimal reparametrizations of shapes

In shape analysis, one of the fundamental problems is to align curves or surfaces before computing a (geodesic) distance between these shapes. To find the optimal reparametrization realizing this alignment is a computationally demanding task which leads to an optimization problem on the diffeomorphism group. In this paper, we construct approximations of orientation-preserving diffeomorphisms by composition of elementary diffeomorphisms to solve the approximation problem. We propose a practical algorithm implemented in PyTorch which is applicable both to unparametrized curves and surfaces. We derive universal approximation results and obtain bounds for the Lipschitz constant of the obtained compositions of diffeomorphisms.

Learning Hamiltonians of constrained mechanical systems

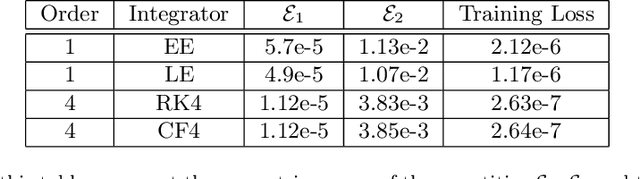
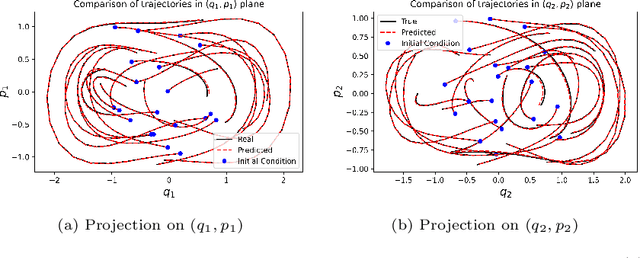
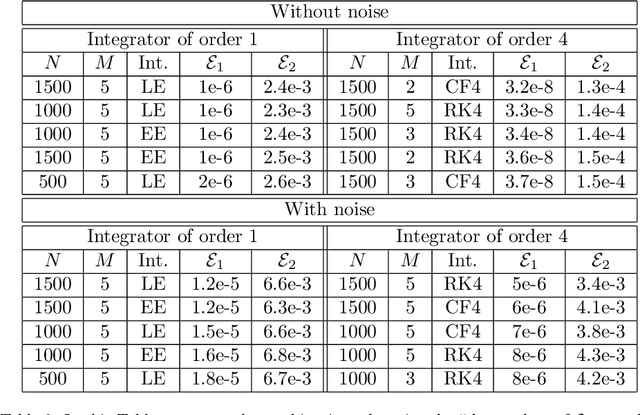
Recently, there has been an increasing interest in modelling and computation of physical systems with neural networks. Hamiltonian systems are an elegant and compact formalism in classical mechanics, where the dynamics is fully determined by one scalar function, the Hamiltonian. The solution trajectories are often constrained to evolve on a submanifold of a linear vector space. In this work, we propose new approaches for the accurate approximation of the Hamiltonian function of constrained mechanical systems given sample data information of their solutions. We focus on the importance of the preservation of the constraints in the learning strategy by using both explicit Lie group integrators and other classical schemes.

Equivariant neural networks for inverse problems

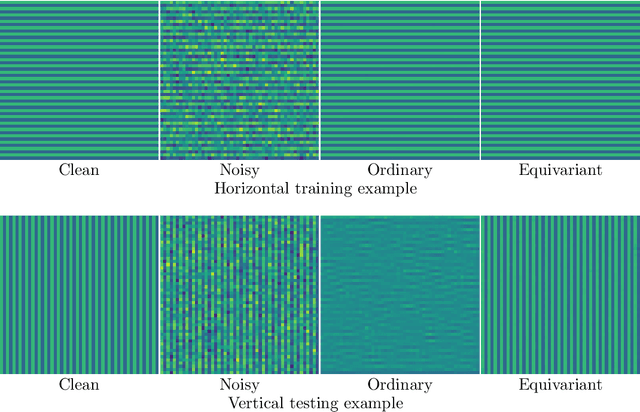
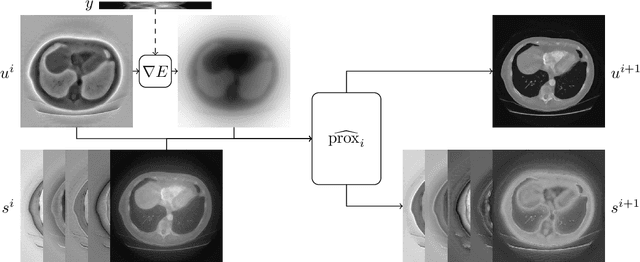
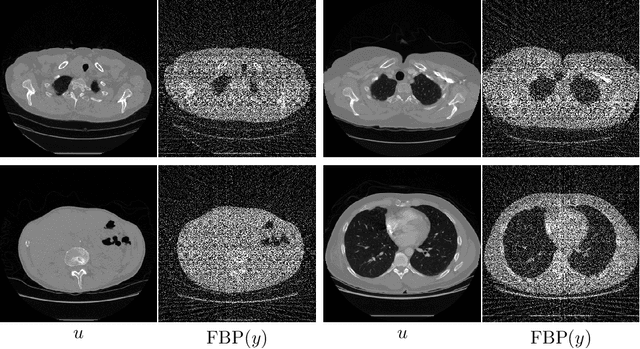
In recent years the use of convolutional layers to encode an inductive bias (translational equivariance) in neural networks has proven to be a very fruitful idea. The successes of this approach have motivated a line of research into incorporating other symmetries into deep learning methods, in the form of group equivariant convolutional neural networks. Much of this work has been focused on roto-translational symmetry of $\mathbf R^d$, but other examples are the scaling symmetry of $\mathbf R^d$ and rotational symmetry of the sphere. In this work, we demonstrate that group equivariant convolutional operations can naturally be incorporated into learned reconstruction methods for inverse problems that are motivated by the variational regularisation approach. Indeed, if the regularisation functional is invariant under a group symmetry, the corresponding proximal operator will satisfy an equivariance property with respect to the same group symmetry. As a result of this observation, we design learned iterative methods in which the proximal operators are modelled as group equivariant convolutional neural networks. We use roto-translationally equivariant operations in the proposed methodology and apply it to the problems of low-dose computerised tomography reconstruction and subsampled magnetic resonance imaging reconstruction. The proposed methodology is demonstrated to improve the reconstruction quality of a learned reconstruction method with a little extra computational cost at training time but without any extra cost at test time.

Structure preserving deep learning

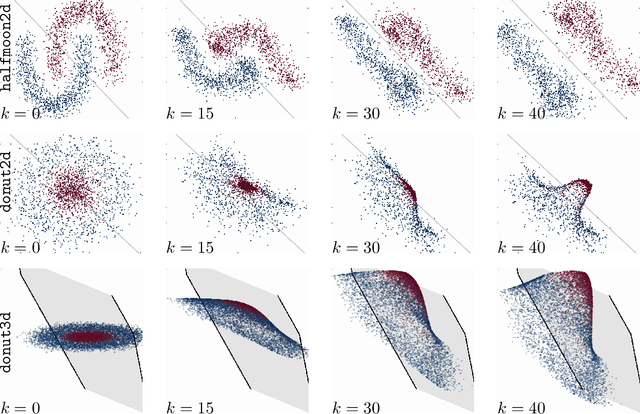
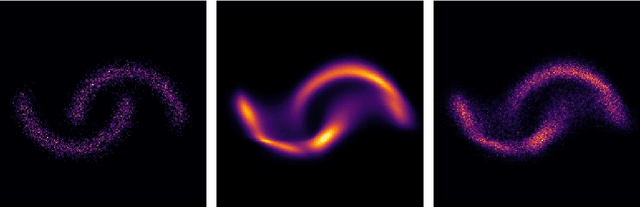
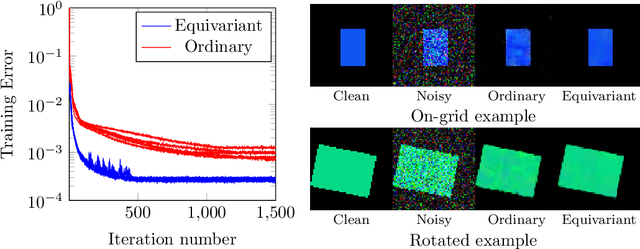
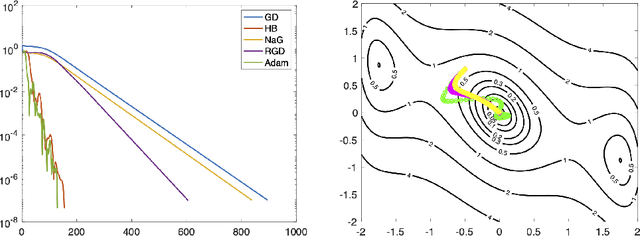
Over the past few years, deep learning has risen to the foreground as a topic of massive interest, mainly as a result of successes obtained in solving large-scale image processing tasks. There are multiple challenging mathematical problems involved in applying deep learning: most deep learning methods require the solution of hard optimisation problems, and a good understanding of the tradeoff between computational effort, amount of data and model complexity is required to successfully design a deep learning approach for a given problem. A large amount of progress made in deep learning has been based on heuristic explorations, but there is a growing effort to mathematically understand the structure in existing deep learning methods and to systematically design new deep learning methods to preserve certain types of structure in deep learning. In this article, we review a number of these directions: some deep neural networks can be understood as discretisations of dynamical systems, neural networks can be designed to have desirable properties such as invertibility or group equivariance, and new algorithmic frameworks based on conformal Hamiltonian systems and Riemannian manifolds to solve the optimisation problems have been proposed. We conclude our review of each of these topics by discussing some open problems that we consider to be interesting directions for future research.

Signatures in Shape Analysis: an Efficient Approach to Motion Identification

Signatures provide a succinct description of certain features of paths in a reparametrization invariant way. We propose a method for classifying shapes based on signatures, and compare it to current approaches based on the SRV transform and dynamic programming.