Supervised Time Series Classification for Anomaly Detection in Subsea Engineering

Time series classification is of significant importance in monitoring structural systems. In this work, we investigate the use of supervised machine learning classification algorithms on simulated data based on a physical system with two states: Intact and Broken. We provide a comprehensive discussion of the preprocessing of temporal data, using measures of statistical dispersion and dimension reduction techniques. We present an intuitive baseline method and discuss its efficiency. We conclude with a comparison of the various methods based on different performance metrics, showing the advantage of using machine learning techniques as a tool in decision making.

Learning Hamiltonians of constrained mechanical systems

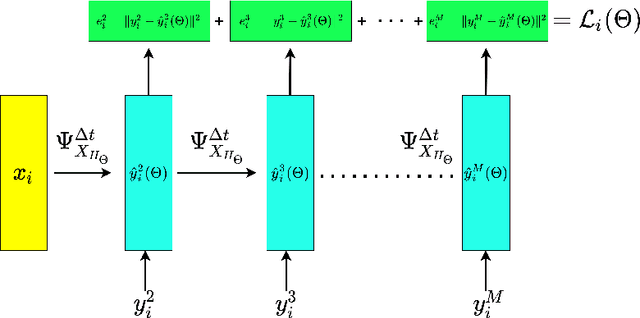
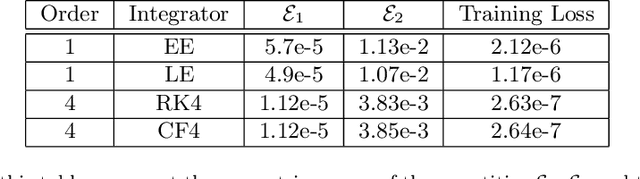
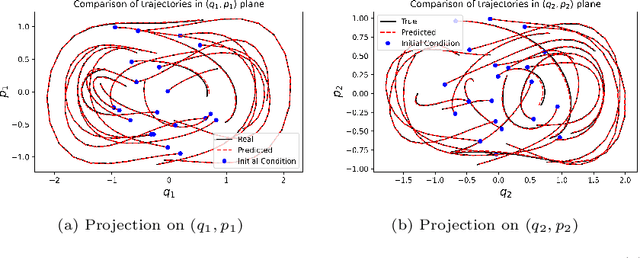
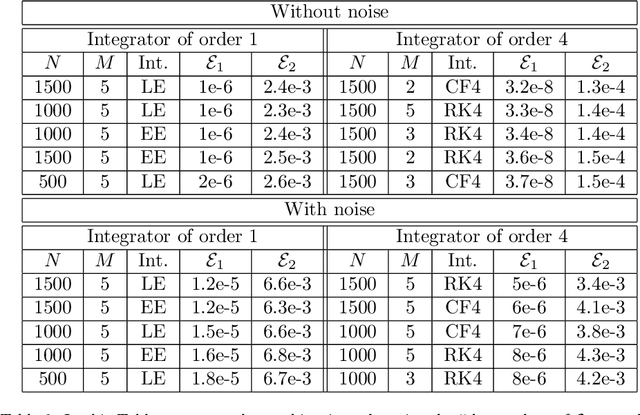
Recently, there has been an increasing interest in modelling and computation of physical systems with neural networks. Hamiltonian systems are an elegant and compact formalism in classical mechanics, where the dynamics is fully determined by one scalar function, the Hamiltonian. The solution trajectories are often constrained to evolve on a submanifold of a linear vector space. In this work, we propose new approaches for the accurate approximation of the Hamiltonian function of constrained mechanical systems given sample data information of their solutions. We focus on the importance of the preservation of the constraints in the learning strategy by using both explicit Lie group integrators and other classical schemes.