Hamiltonian Matching for Symplectic Neural Integrators

Hamilton's equations of motion form a fundamental framework in various branches of physics, including astronomy, quantum mechanics, particle physics, and climate science. Classical numerical solvers are typically employed to compute the time evolution of these systems. However, when the system spans multiple spatial and temporal scales numerical errors can accumulate, leading to reduced accuracy. To address the challenges of evolving such systems over long timescales, we propose SympFlow, a novel neural network-based symplectic integrator, which is the composition of a sequence of exact flow maps of parametrised time-dependent Hamiltonian functions. This architecture allows for a backward error analysis: we can identify an underlying Hamiltonian function of the architecture and use it to define a Hamiltonian matching objective function, which we use for training. In numerical experiments, we show that SympFlow exhibits promising results, with qualitative energy conservation behaviour similar to that of time-stepping symplectic integrators.

Parallel-in-Time Solutions with Random Projection Neural Networks

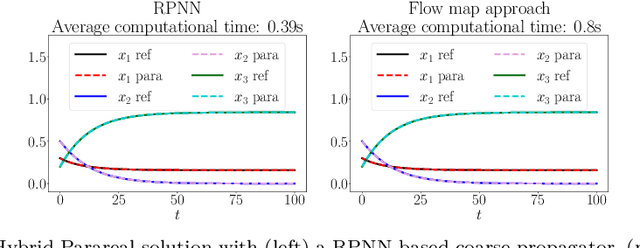
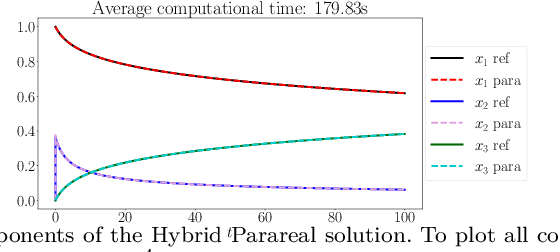
This paper considers one of the fundamental parallel-in-time methods for the solution of ordinary differential equations, Parareal, and extends it by adopting a neural network as a coarse propagator. We provide a theoretical analysis of the convergence properties of the proposed algorithm and show its effectiveness for several examples, including Lorenz and Burgers' equations. In our numerical simulations, we further specialize the underpinning neural architecture to Random Projection Neural Networks (RPNNs), a 2-layer neural network where the first layer weights are drawn at random rather than optimized. This restriction substantially increases the efficiency of fitting RPNN's weights in comparison to a standard feedforward network without negatively impacting the accuracy, as demonstrated in the SIR system example.

Contractive Systems Improve Graph Neural Networks Against Adversarial Attacks

Graph Neural Networks (GNNs) have established themselves as a key component in addressing diverse graph-based tasks. Despite their notable successes, GNNs remain susceptible to input perturbations in the form of adversarial attacks. This paper introduces an innovative approach to fortify GNNs against adversarial perturbations through the lens of contractive dynamical systems. Our method introduces graph neural layers based on differential equations with contractive properties, which, as we show, improve the robustness of GNNs. A distinctive feature of the proposed approach is the simultaneous learned evolution of both the node features and the adjacency matrix, yielding an intrinsic enhancement of model robustness to perturbations in the input features and the connectivity of the graph. We mathematically derive the underpinnings of our novel architecture and provide theoretical insights to reason about its expected behavior. We demonstrate the efficacy of our method through numerous real-world benchmarks, reading on par or improved performance compared to existing methods.

Designing Stable Neural Networks using Convex Analysis and ODEs

Motivated by classical work on the numerical integration of ordinary differential equations we present a ResNet-styled neural network architecture that encodes non-expansive (1-Lipschitz) operators, as long as the spectral norms of the weights are appropriately constrained. This is to be contrasted with the ordinary ResNet architecture which, even if the spectral norms of the weights are constrained, has a Lipschitz constant that, in the worst case, grows exponentially with the depth of the network. Further analysis of the proposed architecture shows that the spectral norms of the weights can be further constrained to ensure that the network is an averaged operator, making it a natural candidate for a learned denoiser in Plug-and-Play algorithms. Using a novel adaptive way of enforcing the spectral norm constraints, we show that, even with these constraints, it is possible to train performant networks. The proposed architecture is applied to the problem of adversarially robust image classification, to image denoising, and finally to the inverse problem of deblurring.

Predictions Based on Pixel Data: Insights from PDEs and Finite Differences

Neural networks are the state-of-the-art for many approximation tasks in high-dimensional spaces, as supported by an abundance of experimental evidence. However, we still need a solid theoretical understanding of what they can approximate and, more importantly, at what cost and accuracy. One network architecture of practical use, especially for approximation tasks involving images, is convolutional (residual) networks. However, due to the locality of the linear operators involved in these networks, their analysis is more complicated than for generic fully connected neural networks. This paper focuses on sequence approximation tasks, where a matrix or a higher-order tensor represents each observation. We show that when approximating sequences arising from space-time discretisations of PDEs we may use relatively small networks. We constructively derive these results by exploiting connections between discrete convolution and finite difference operators. Throughout, we design our network architecture to, while having guarantees, be similar to those typically adopted in practice for sequence approximation tasks. Our theoretical results are supported by numerical experiments which simulate linear advection, the heat equation, and the Fisher equation. The implementation used is available at the repository associated to the paper.

Dynamical systems' based neural networks

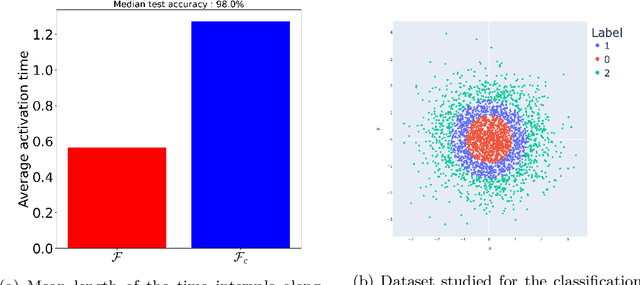
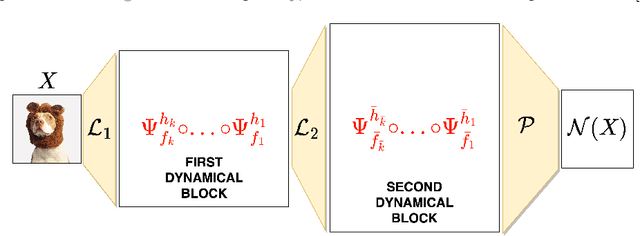
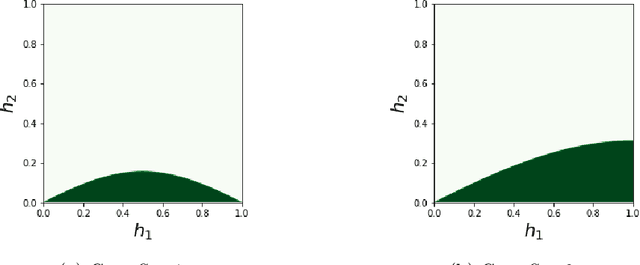
Neural networks have gained much interest because of their effectiveness in many applications. However, their mathematical properties are generally not well understood. If there is some underlying geometric structure inherent to the data or to the function to approximate, it is often desirable to take this into account in the design of the neural network. In this work, we start with a non-autonomous ODE and build neural networks using a suitable, structure-preserving, numerical time-discretisation. The structure of the neural network is then inferred from the properties of the ODE vector field. Besides injecting more structure into the network architectures, this modelling procedure allows a better theoretical understanding of their behaviour. We present two universal approximation results and demonstrate how to impose some particular properties on the neural networks. A particular focus is on 1-Lipschitz architectures including layers that are not 1-Lipschitz. These networks are expressive and robust against adversarial attacks, as shown for the CIFAR-10 dataset.

Learning Hamiltonians of constrained mechanical systems

Recently, there has been an increasing interest in modelling and computation of physical systems with neural networks. Hamiltonian systems are an elegant and compact formalism in classical mechanics, where the dynamics is fully determined by one scalar function, the Hamiltonian. The solution trajectories are often constrained to evolve on a submanifold of a linear vector space. In this work, we propose new approaches for the accurate approximation of the Hamiltonian function of constrained mechanical systems given sample data information of their solutions. We focus on the importance of the preservation of the constraints in the learning strategy by using both explicit Lie group integrators and other classical schemes.