Revisiting Node Affinity Prediction in Temporal Graphs

Node affinity prediction is a common task that is widely used in temporal graph learning with applications in social and financial networks, recommender systems, and more. Recent works have addressed this task by adapting state-of-the-art dynamic link property prediction models to node affinity prediction. However, simple heuristics, such as Persistent Forecast or Moving Average, outperform these models. In this work, we analyze the challenges in training current Temporal Graph Neural Networks for node affinity prediction and suggest appropriate solutions. Combining the solutions, we develop NAViS - Node Affinity prediction model using Virtual State, by exploiting the equivalence between heuristics and state space models. While promising, training NAViS is non-trivial. Therefore, we further introduce a novel loss function for node affinity prediction. We evaluate NAViS on TGB and show that it outperforms the state-of-the-art, including heuristics. Our source code is available at https://github.com/orfeld415/NAVIS

TANGO: Graph Neural Dynamics via Learned Energy and Tangential Flows

We introduce TANGO -- a dynamical systems inspired framework for graph representation learning that governs node feature evolution through a learned energy landscape and its associated descent dynamics. At the core of our approach is a learnable Lyapunov function over node embeddings, whose gradient defines an energy-reducing direction that guarantees convergence and stability. To enhance flexibility while preserving the benefits of energy-based dynamics, we incorporate a novel tangential component, learned via message passing, that evolves features while maintaining the energy value. This decomposition into orthogonal flows of energy gradient descent and tangential evolution yields a flexible form of graph dynamics, and enables effective signal propagation even in flat or ill-conditioned energy regions, that often appear in graph learning. Our method mitigates oversquashing and is compatible with different graph neural network backbones. Empirically, TANGO achieves strong performance across a diverse set of node and graph classification and regression benchmarks, demonstrating the effectiveness of jointly learned energy functions and tangential flows for graph neural networks.

Return of ChebNet: Understanding and Improving an Overlooked GNN on Long Range Tasks

ChebNet, one of the earliest spectral GNNs, has largely been overshadowed by Message Passing Neural Networks (MPNNs), which gained popularity for their simplicity and effectiveness in capturing local graph structure. Despite their success, MPNNs are limited in their ability to capture long-range dependencies between nodes. This has led researchers to adapt MPNNs through rewiring or make use of Graph Transformers, which compromises the computational efficiency that characterized early spatial message-passing architectures, and typically disregards the graph structure. Almost a decade after its original introduction, we revisit ChebNet to shed light on its ability to model distant node interactions. We find that out-of-box, ChebNet already shows competitive advantages relative to classical MPNNs and GTs on long-range benchmarks, while maintaining good scalability properties for high-order polynomials. However, we uncover that this polynomial expansion leads ChebNet to an unstable regime during training. To address this limitation, we cast ChebNet as a stable and non-dissipative dynamical system, which we coin Stable-ChebNet. Our Stable-ChebNet model allows for stable information propagation, and has controllable dynamics which do not require the use of eigendecompositions, positional encodings, or graph rewiring. Across several benchmarks, Stable-ChebNet achieves near state-of-the-art performance.

Graph Flow Matching: Enhancing Image Generation with Neighbor-Aware Flow Fields

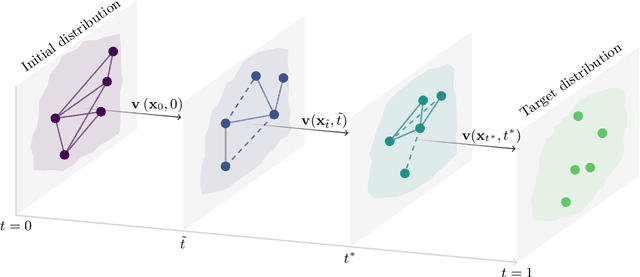
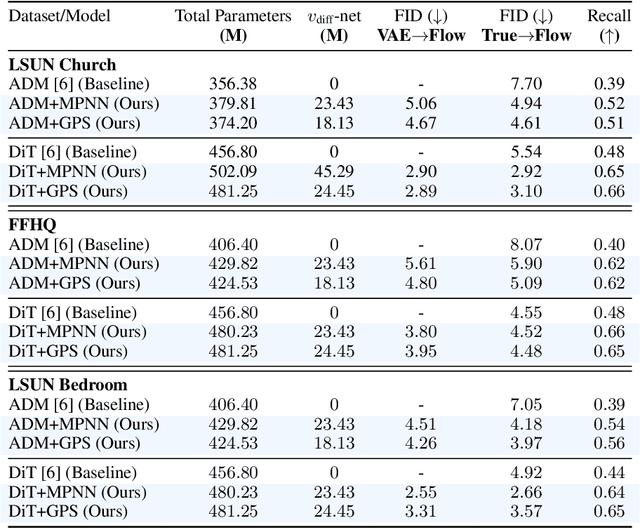
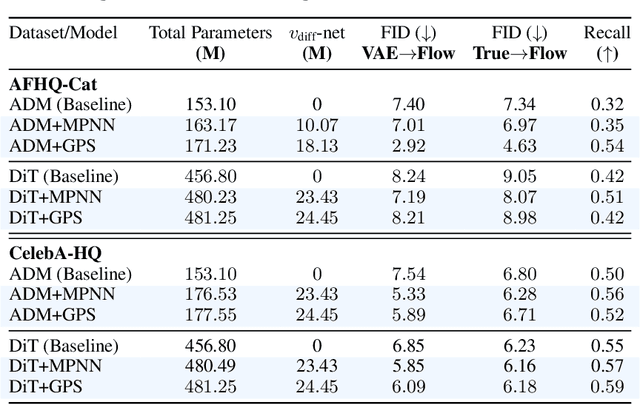
Flow matching casts sample generation as learning a continuous-time velocity field that transports noise to data. Existing flow matching networks typically predict each point's velocity independently, considering only its location and time along its flow trajectory, and ignoring neighboring points. However, this pointwise approach may overlook correlations between points along the generation trajectory that could enhance velocity predictions, thereby improving downstream generation quality. To address this, we propose Graph Flow Matching (GFM), a lightweight enhancement that decomposes the learned velocity into a reaction term -- any standard flow matching network -- and a diffusion term that aggregates neighbor information via a graph neural module. This reaction-diffusion formulation retains the scalability of deep flow models while enriching velocity predictions with local context, all at minimal additional computational cost. Operating in the latent space of a pretrained variational autoencoder, GFM consistently improves Fr\'echet Inception Distance (FID) and recall across five image generation benchmarks (LSUN Church, LSUN Bedroom, FFHQ, AFHQ-Cat, and CelebA-HQ at $256\times256$), demonstrating its effectiveness as a modular enhancement to existing flow matching architectures.

Improving the Effective Receptive Field of Message-Passing Neural Networks

Message-Passing Neural Networks (MPNNs) have become a cornerstone for processing and analyzing graph-structured data. However, their effectiveness is often hindered by phenomena such as over-squashing, where long-range dependencies or interactions are inadequately captured and expressed in the MPNN output. This limitation mirrors the challenges of the Effective Receptive Field (ERF) in Convolutional Neural Networks (CNNs), where the theoretical receptive field is underutilized in practice. In this work, we show and theoretically explain the limited ERF problem in MPNNs. Furthermore, inspired by recent advances in ERF augmentation for CNNs, we propose an Interleaved Multiscale Message-Passing Neural Networks (IM-MPNN) architecture to address these problems in MPNNs. Our method incorporates a hierarchical coarsening of the graph, enabling message-passing across multiscale representations and facilitating long-range interactions without excessive depth or parameterization. Through extensive evaluations on benchmarks such as the Long-Range Graph Benchmark (LRGB), we demonstrate substantial improvements over baseline MPNNs in capturing long-range dependencies while maintaining computational efficiency.

Message-Passing State-Space Models: Improving Graph Learning with Modern Sequence Modeling

The recent success of State-Space Models (SSMs) in sequence modeling has motivated their adaptation to graph learning, giving rise to Graph State-Space Models (GSSMs). However, existing GSSMs operate by applying SSM modules to sequences extracted from graphs, often compromising core properties such as permutation equivariance, message-passing compatibility, and computational efficiency. In this paper, we introduce a new perspective by embedding the key principles of modern SSM computation directly into the Message-Passing Neural Network framework, resulting in a unified methodology for both static and temporal graphs. Our approach, MP-SSM, enables efficient, permutation-equivariant, and long-range information propagation while preserving the architectural simplicity of message passing. Crucially, MP-SSM enables an exact sensitivity analysis, which we use to theoretically characterize information flow and evaluate issues like vanishing gradients and over-squashing in the deep regime. Furthermore, our design choices allow for a highly optimized parallel implementation akin to modern SSMs. We validate MP-SSM across a wide range of tasks, including node classification, graph property prediction, long-range benchmarks, and spatiotemporal forecasting, demonstrating both its versatility and strong empirical performance.

One-Step Offline Distillation of Diffusion-based Models via Koopman Modeling

Diffusion-based generative models have demonstrated exceptional performance, yet their iterative sampling procedures remain computationally expensive. A prominent strategy to mitigate this cost is distillation, with offline distillation offering particular advantages in terms of efficiency, modularity, and flexibility. In this work, we identify two key observations that motivate a principled distillation framework: (1) while diffusion models have been viewed through the lens of dynamical systems theory, powerful and underexplored tools can be further leveraged; and (2) diffusion models inherently impose structured, semantically coherent trajectories in latent space. Building on these observations, we introduce the Koopman Distillation Model KDM, a novel offline distillation approach grounded in Koopman theory-a classical framework for representing nonlinear dynamics linearly in a transformed space. KDM encodes noisy inputs into an embedded space where a learned linear operator propagates them forward, followed by a decoder that reconstructs clean samples. This enables single-step generation while preserving semantic fidelity. We provide theoretical justification for our approach: (1) under mild assumptions, the learned diffusion dynamics admit a finite-dimensional Koopman representation; and (2) proximity in the Koopman latent space correlates with semantic similarity in the generated outputs, allowing for effective trajectory alignment. Empirically, KDM achieves state-of-the-art performance across standard offline distillation benchmarks, improving FID scores by up to 40% in a single generation step. All implementation details and code for the experimental setups are provided in our GitHub - https://github.com/azencot-group/KDM, or in our project page - https://sites.google.com/view/koopman-distillation-model.

FLASH: Flexible Learning of Adaptive Sampling from History in Temporal Graph Neural Networks

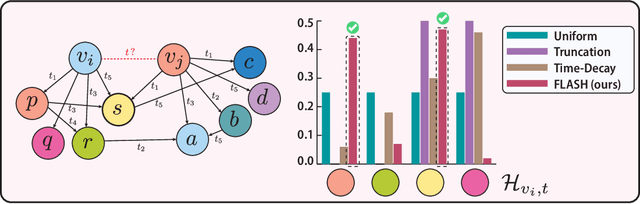
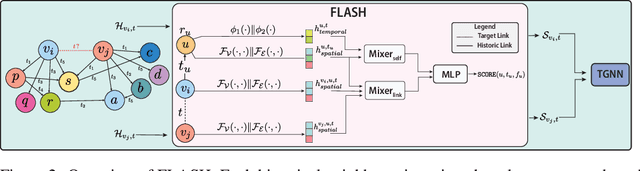
Aggregating temporal signals from historic interactions is a key step in future link prediction on dynamic graphs. However, incorporating long histories is resource-intensive. Hence, temporal graph neural networks (TGNNs) often rely on historical neighbors sampling heuristics such as uniform sampling or recent neighbors selection. These heuristics are static and fail to adapt to the underlying graph structure. We introduce FLASH, a learnable and graph-adaptive neighborhood selection mechanism that generalizes existing heuristics. FLASH integrates seamlessly into TGNNs and is trained end-to-end using a self-supervised ranking loss. We provide theoretical evidence that commonly used heuristics hinders TGNNs performance, motivating our design. Extensive experiments across multiple benchmarks demonstrate consistent and significant performance improvements for TGNNs equipped with FLASH.

Towards Efficient Training of Graph Neural Networks: A Multiscale Approach

Graph Neural Networks (GNNs) have emerged as a powerful tool for learning and inferring from graph-structured data, and are widely used in a variety of applications, often considering large amounts of data and large graphs. However, training on such data requires large memory and extensive computations. In this paper, we introduce a novel framework for efficient multiscale training of GNNs, designed to integrate information across multiscale representations of a graph. Our approach leverages a hierarchical graph representation, taking advantage of coarse graph scales in the training process, where each coarse scale graph has fewer nodes and edges. Based on this approach, we propose a suite of GNN training methods: such as coarse-to-fine, sub-to-full, and multiscale gradient computation. We demonstrate the effectiveness of our methods on various datasets and learning tasks.

Iterative Flow Matching -- Path Correction and Gradual Refinement for Enhanced Generative Modeling

Generative models for image generation are now commonly used for a wide variety of applications, ranging from guided image generation for entertainment to solving inverse problems. Nonetheless, training a generator is a non-trivial feat that requires fine-tuning and can lead to so-called hallucinations, that is, the generation of images that are unrealistic. In this work, we explore image generation using flow matching. We explain and demonstrate why flow matching can generate hallucinations, and propose an iterative process to improve the generation process. Our iterative process can be integrated into virtually $\textit{any}$ generative modeling technique, thereby enhancing the performance and robustness of image synthesis systems.