Learning to Advect: A Neural Semi-Lagrangian Architecture for Weather Forecasting

Recent machine-learning approaches to weather forecasting often employ a monolithic architecture, where distinct physical mechanisms (advection, transport), diffusion-like mixing, thermodynamic processes, and forcing are represented implicitly within a single large network. This representation is particularly problematic for advection, where long-range transport must be treated with expensive global interaction mechanisms or through deep, stacked convolutional layers. To mitigate this, we present PARADIS, a physics-inspired global weather prediction model that imposes inductive biases on network behavior through a functional decomposition into advection, diffusion, and reaction blocks acting on latent variables. We implement advection through a Neural Semi-Lagrangian operator that performs trajectory-based transport via differentiable interpolation on the sphere, enabling end-to-end learning of both the latent modes to be transported and their characteristic trajectories. Diffusion-like processes are modeled through depthwise-separable spatial mixing, while local source terms and vertical interactions are modeled via pointwise channel interactions, enabling operator-level physical structure. PARADIS provides state-of-the-art forecast skill at a fraction of the training cost. On ERA5-based benchmarks, the 1 degree PARADIS model, with a total training cost of less than a GPU month, meets or exceeds the performance of 0.25 degree traditional and machine-learning baselines, including the ECMWF HRES forecast and DeepMind's GraphCast.

TANGO: Graph Neural Dynamics via Learned Energy and Tangential Flows

We introduce TANGO -- a dynamical systems inspired framework for graph representation learning that governs node feature evolution through a learned energy landscape and its associated descent dynamics. At the core of our approach is a learnable Lyapunov function over node embeddings, whose gradient defines an energy-reducing direction that guarantees convergence and stability. To enhance flexibility while preserving the benefits of energy-based dynamics, we incorporate a novel tangential component, learned via message passing, that evolves features while maintaining the energy value. This decomposition into orthogonal flows of energy gradient descent and tangential evolution yields a flexible form of graph dynamics, and enables effective signal propagation even in flat or ill-conditioned energy regions, that often appear in graph learning. Our method mitigates oversquashing and is compatible with different graph neural network backbones. Empirically, TANGO achieves strong performance across a diverse set of node and graph classification and regression benchmarks, demonstrating the effectiveness of jointly learned energy functions and tangential flows for graph neural networks.

Synthetic Geology -- Structural Geology Meets Deep Learning

Visualizing the first few kilometers of the Earth's subsurface, a long-standing challenge gating a virtually inexhaustible list of important applications, is coming within reach through deep learning. Building on techniques of generative artificial intelligence applied to voxelated images, we demonstrate a method that extends surface geological data supplemented by boreholes to a three-dimensional subsurface region by training a neural network. The Earth's land area having been extensively mapped for geological features, the bottleneck of this or any related technique is the availability of data below the surface. We close this data gap in the development of subsurface deep learning by designing a synthetic data-generator process that mimics eons of geological activity such as sediment compaction, volcanic intrusion, and tectonic dynamics to produce a virtually limitless number of samples of the near lithosphere. A foundation model trained on such synthetic data is able to generate a 3D image of the subsurface from a previously unseen map of surface topography and geology, showing increasing fidelity with increasing access to borehole data, depicting such structures as layers, faults, folds, dikes, and sills. We illustrate the early promise of the combination of a synthetic lithospheric generator with a trained neural network model using generative flow matching. Ultimately, such models will be fine-tuned on data from applicable campaigns, such as mineral prospecting in a given region. Though useful in itself, a regionally fine-tuned models may be employed not as an end but as a means: as an AI-based regularizer in a more traditional inverse problem application, in which the objective function represents the mismatch of additional data with physical models with applications in resource exploration, hazard assessment, and geotechnical engineering.

Graph Flow Matching: Enhancing Image Generation with Neighbor-Aware Flow Fields

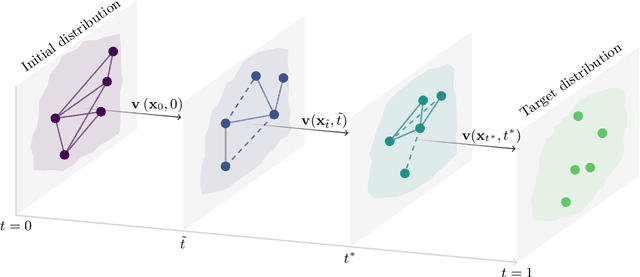
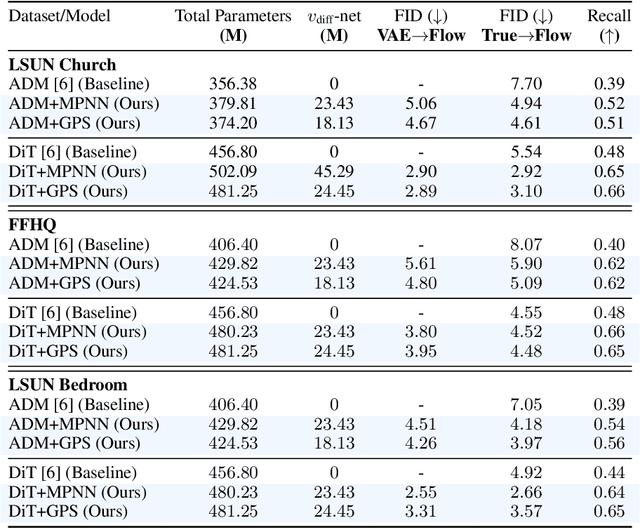
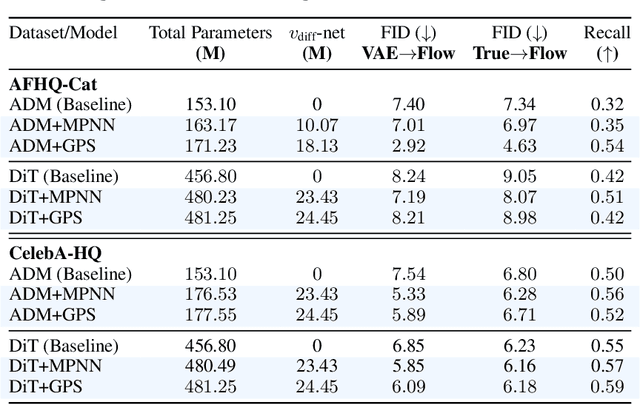
Flow matching casts sample generation as learning a continuous-time velocity field that transports noise to data. Existing flow matching networks typically predict each point's velocity independently, considering only its location and time along its flow trajectory, and ignoring neighboring points. However, this pointwise approach may overlook correlations between points along the generation trajectory that could enhance velocity predictions, thereby improving downstream generation quality. To address this, we propose Graph Flow Matching (GFM), a lightweight enhancement that decomposes the learned velocity into a reaction term -- any standard flow matching network -- and a diffusion term that aggregates neighbor information via a graph neural module. This reaction-diffusion formulation retains the scalability of deep flow models while enriching velocity predictions with local context, all at minimal additional computational cost. Operating in the latent space of a pretrained variational autoencoder, GFM consistently improves Fr\'echet Inception Distance (FID) and recall across five image generation benchmarks (LSUN Church, LSUN Bedroom, FFHQ, AFHQ-Cat, and CelebA-HQ at $256\times256$), demonstrating its effectiveness as a modular enhancement to existing flow matching architectures.

Towards Efficient Training of Graph Neural Networks: A Multiscale Approach

Graph Neural Networks (GNNs) have emerged as a powerful tool for learning and inferring from graph-structured data, and are widely used in a variety of applications, often considering large amounts of data and large graphs. However, training on such data requires large memory and extensive computations. In this paper, we introduce a novel framework for efficient multiscale training of GNNs, designed to integrate information across multiscale representations of a graph. Our approach leverages a hierarchical graph representation, taking advantage of coarse graph scales in the training process, where each coarse scale graph has fewer nodes and edges. Based on this approach, we propose a suite of GNN training methods: such as coarse-to-fine, sub-to-full, and multiscale gradient computation. We demonstrate the effectiveness of our methods on various datasets and learning tasks.

Probabilistic Forecasting for Dynamical Systems with Missing or Imperfect Data

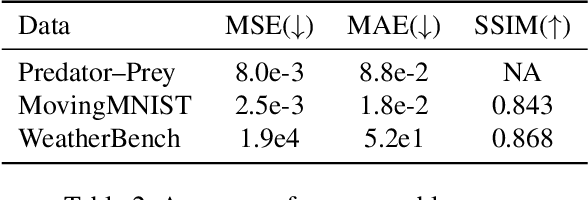
The modeling of dynamical systems is essential in many fields, but applying machine learning techniques is often challenging due to incomplete or noisy data. This study introduces a variant of stochastic interpolation (SI) for probabilistic forecasting, estimating future states as distributions rather than single-point predictions. We explore its mathematical foundations and demonstrate its effectiveness on various dynamical systems, including the challenging WeatherBench dataset.

Iterative Flow Matching -- Path Correction and Gradual Refinement for Enhanced Generative Modeling

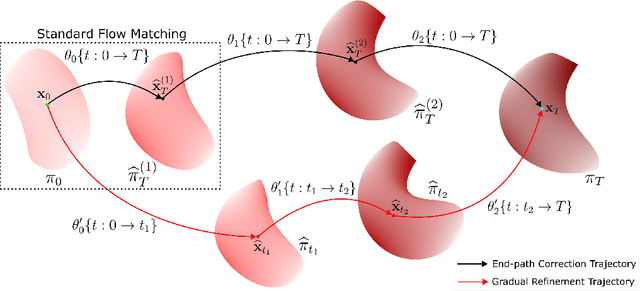
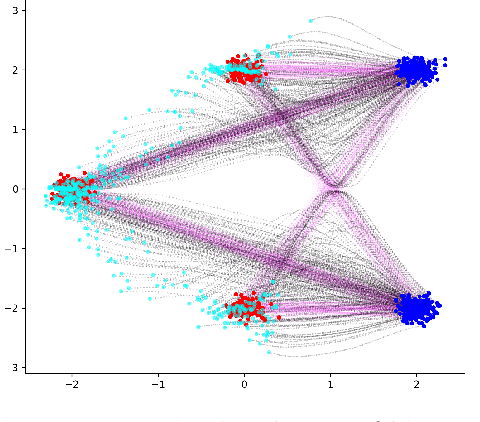
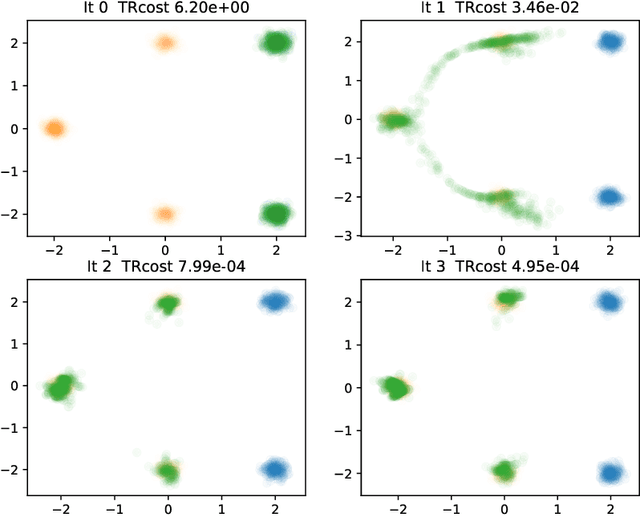
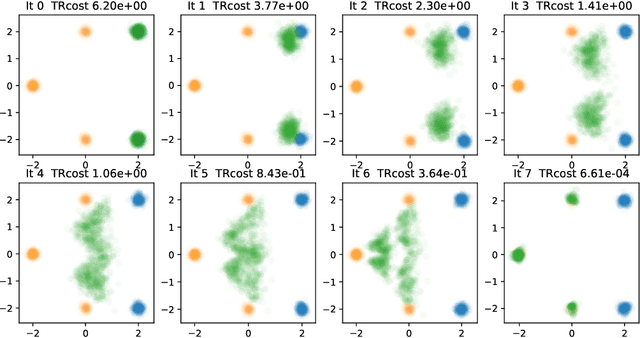
Generative models for image generation are now commonly used for a wide variety of applications, ranging from guided image generation for entertainment to solving inverse problems. Nonetheless, training a generator is a non-trivial feat that requires fine-tuning and can lead to so-called hallucinations, that is, the generation of images that are unrealistic. In this work, we explore image generation using flow matching. We explain and demonstrate why flow matching can generate hallucinations, and propose an iterative process to improve the generation process. Our iterative process can be integrated into virtually $\textit{any}$ generative modeling technique, thereby enhancing the performance and robustness of image synthesis systems.

Inversion of Magnetic Data using Learned Dictionaries and Scale Space

Magnetic data inversion is an important tool in geophysics, used to infer subsurface magnetic susceptibility distributions from surface magnetic field measurements. This inverse problem is inherently ill-posed, characterized by non-unique solutions, depth ambiguity, and sensitivity to noise. Traditional inversion approaches rely on predefined regularization techniques to stabilize solutions, limiting their adaptability to complex or diverse geological scenarios. In this study, we propose an approach that integrates variable dictionary learning and scale-space methods to address these challenges. Our method employs learned dictionaries, allowing for adaptive representation of complex subsurface features that are difficult to capture with predefined bases. Additionally, we extend classical variational inversion by incorporating multi-scale representations through a scale-space framework, enabling the progressive introduction of structural detail while mitigating overfitting. We implement both fixed and dynamic dictionary learning techniques, with the latter introducing iteration-dependent dictionaries for enhanced flexibility. Using a synthetic dataset to simulate geological scenarios, we demonstrate significant improvements in reconstruction accuracy and robustness compared to conventional variational and dictionary-based methods. Our results highlight the potential of learned dictionaries, especially when coupled with scale-space dynamics, to improve model recovery and noise handling. These findings underscore the promise of our data-driven approach for advance magnetic data inversion and its applications in geophysical exploration, environmental assessment, and mineral prospecting.

DAWN-SI: Data-Aware and Noise-Informed Stochastic Interpolation for Solving Inverse Problems

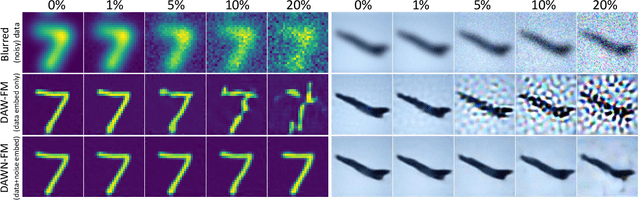
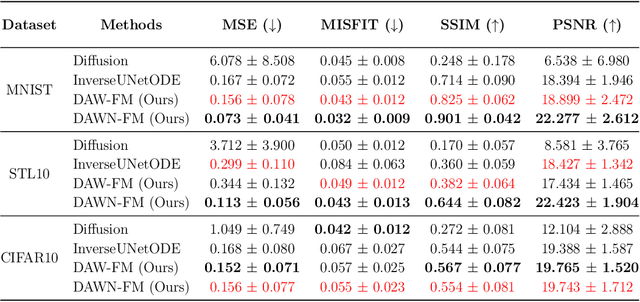
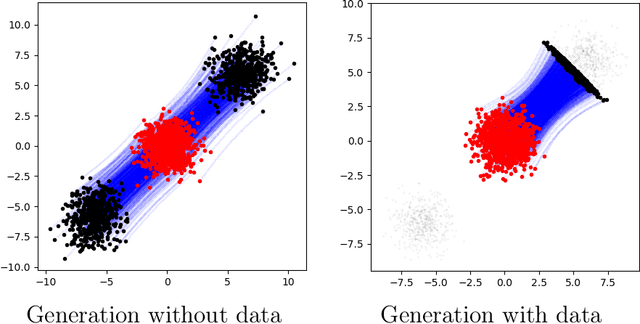
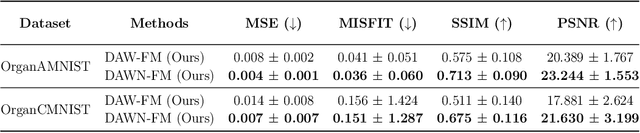
Inverse problems, which involve estimating parameters from incomplete or noisy observations, arise in various fields such as medical imaging, geophysics, and signal processing. These problems are often ill-posed, requiring regularization techniques to stabilize the solution. In this work, we employ $\textit{Stochastic Interpolation}$ (SI), a generative framework that integrates both deterministic and stochastic processes to map a simple reference distribution, such as a Gaussian, to the target distribution. Our method $\textbf{DAWN-SI}$: $\textbf{D}$ata-$\textbf{AW}$are and $\textbf{N}$oise-informed $\textbf{S}$tochastic $\textbf{I}$nterpolation incorporates data and noise embedding, allowing the model to access representations about the measured data explicitly and also account for noise in the observations, making it particularly robust in scenarios where data is noisy or incomplete. By learning a time-dependent velocity field, SI not only provides accurate solutions but also enables uncertainty quantification by generating multiple plausible outcomes. Unlike pre-trained diffusion models, which may struggle in highly ill-posed settings, our approach is trained specifically for each inverse problem and adapts to varying noise levels. We validate the effectiveness and robustness of our method through extensive numerical experiments on tasks such as image deblurring and tomography.

Learning Regularization for Graph Inverse Problems

In recent years, Graph Neural Networks (GNNs) have been utilized for various applications ranging from drug discovery to network design and social networks. In many applications, it is impossible to observe some properties of the graph directly; instead, noisy and indirect measurements of these properties are available. These scenarios are coined as Graph Inverse Problems (GRIP). In this work, we introduce a framework leveraging GNNs to solve GRIPs. The framework is based on a combination of likelihood and prior terms, which are used to find a solution that fits the data while adhering to learned prior information. Specifically, we propose to combine recent deep learning techniques that were developed for inverse problems, together with GNN architectures, to formulate and solve GRIP. We study our approach on a number of representative problems that demonstrate the effectiveness of the framework.