DEF: Diffusion-augmented Ensemble Forecasting

We present DEF (\textbf{\ul{D}}iffusion-augmented \textbf{\ul{E}}nsemble \textbf{\ul{F}}orecasting), a novel approach for generating initial condition perturbations. Modern approaches to initial condition perturbations are primarily designed for numerical weather prediction (NWP) solvers, limiting their applicability in the rapidly growing field of machine learning for weather prediction. Consequently, stochastic models in this domain are often developed on a case-by-case basis. We demonstrate that a simple conditional diffusion model can (1) generate meaningful structured perturbations, (2) be applied iteratively, and (3) utilize a guidance term to intuitivey control the level of perturbation. This method enables the transformation of any deterministic neural forecasting system into a stochastic one. With our stochastic extended systems, we show that the model accumulates less error over long-term forecasts while producing meaningful forecast distributions. We validate our approach on the 5.625$^\circ$ ERA5 reanalysis dataset, which comprises atmospheric and surface variables over a discretized global grid, spanning from the 1960s to the present. On this dataset, our method demonstrates improved predictive performance along with reasonable spread estimates.

Probabilistic Forecasting for Dynamical Systems with Missing or Imperfect Data

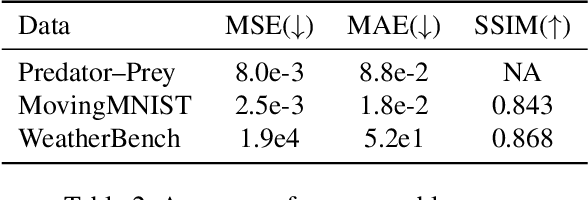
The modeling of dynamical systems is essential in many fields, but applying machine learning techniques is often challenging due to incomplete or noisy data. This study introduces a variant of stochastic interpolation (SI) for probabilistic forecasting, estimating future states as distributions rather than single-point predictions. We explore its mathematical foundations and demonstrate its effectiveness on various dynamical systems, including the challenging WeatherBench dataset.

PEARL: Preconditioner Enhancement through Actor-critic Reinforcement Learning

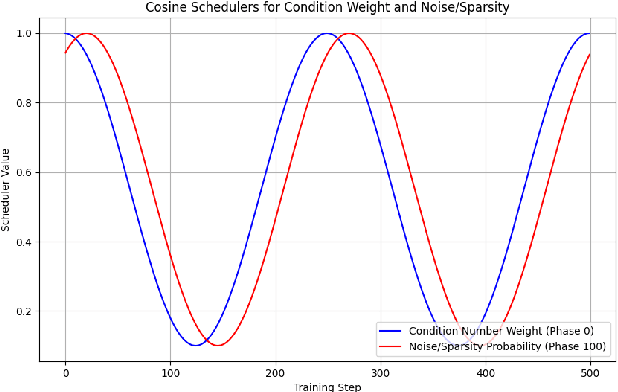
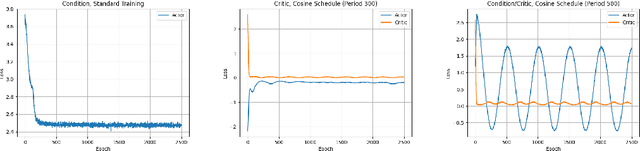
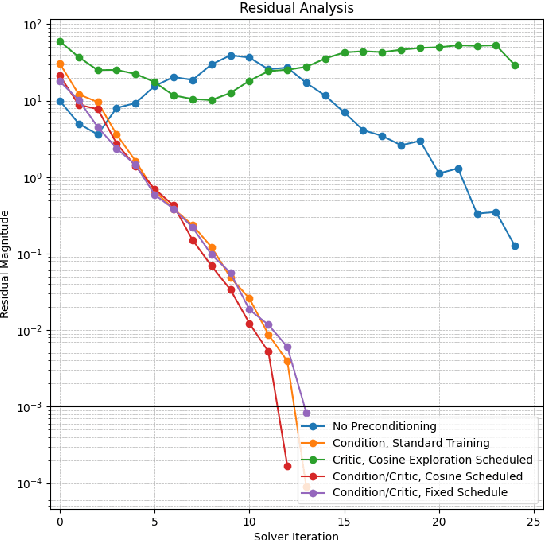
We present PEARL (Preconditioner Enhancement through Actor-critic Reinforcement Learning), a novel approach to learning matrix preconditioners. Existing preconditioners such as Jacobi, Incomplete LU, and Algebraic Multigrid methods offer problem-specific advantages but rely heavily on hyperparameter tuning. Recent advances have explored using deep neural networks to learn preconditioners, though challenges such as misbehaved objective functions and costly training procedures remain. PEARL introduces a reinforcement learning approach for learning preconditioners, specifically, a contextual bandit formulation. The framework utilizes an actor-critic model, where the actor generates the incomplete Cholesky decomposition of preconditioners, and the critic evaluates them based on reward-specific feedback. To further guide the training, we design a dual-objective function, combining updates from the critic and condition number. PEARL contributes a generalizable preconditioner learning method, dynamic sparsity exploration, and cosine schedulers for improved stability and exploratory power. We compare our approach to traditional and neural preconditioners, demonstrating improved flexibility and iterative solving speed.

Deep Learning for Koopman Operator Estimation in Idealized Atmospheric Dynamics

Deep learning is revolutionizing weather forecasting, with new data-driven models achieving accuracy on par with operational physical models for medium-term predictions. However, these models often lack interpretability, making their underlying dynamics difficult to understand and explain. This paper proposes methodologies to estimate the Koopman operator, providing a linear representation of complex nonlinear dynamics to enhance the transparency of data-driven models. Despite its potential, applying the Koopman operator to large-scale problems, such as atmospheric modeling, remains challenging. This study aims to identify the limitations of existing methods, refine these models to overcome various bottlenecks, and introduce novel convolutional neural network architectures that capture simplified dynamics.