Arielle Carr
DEF: Diffusion-augmented Ensemble Forecasting
Jun 08, 2025Abstract:We present DEF (\textbf{\ul{D}}iffusion-augmented \textbf{\ul{E}}nsemble \textbf{\ul{F}}orecasting), a novel approach for generating initial condition perturbations. Modern approaches to initial condition perturbations are primarily designed for numerical weather prediction (NWP) solvers, limiting their applicability in the rapidly growing field of machine learning for weather prediction. Consequently, stochastic models in this domain are often developed on a case-by-case basis. We demonstrate that a simple conditional diffusion model can (1) generate meaningful structured perturbations, (2) be applied iteratively, and (3) utilize a guidance term to intuitivey control the level of perturbation. This method enables the transformation of any deterministic neural forecasting system into a stochastic one. With our stochastic extended systems, we show that the model accumulates less error over long-term forecasts while producing meaningful forecast distributions. We validate our approach on the 5.625$^\circ$ ERA5 reanalysis dataset, which comprises atmospheric and surface variables over a discretized global grid, spanning from the 1960s to the present. On this dataset, our method demonstrates improved predictive performance along with reasonable spread estimates.
PEARL: Preconditioner Enhancement through Actor-critic Reinforcement Learning
Jan 18, 2025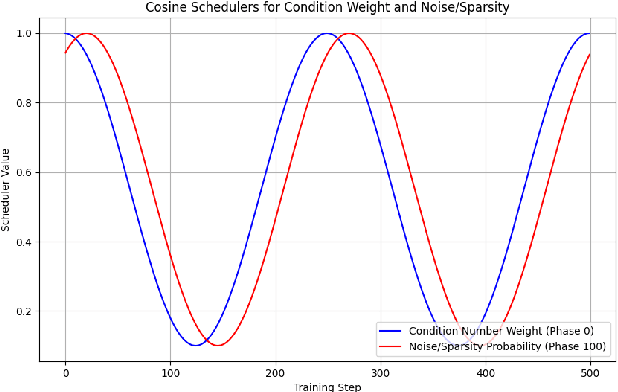

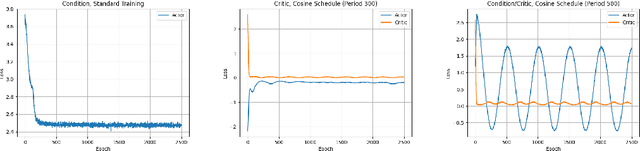
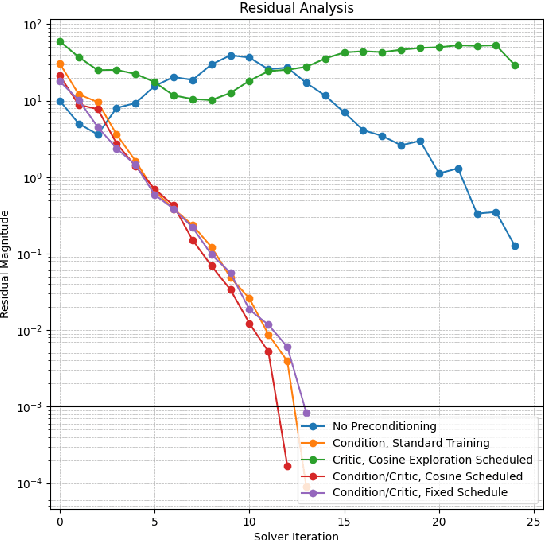
Abstract:We present PEARL (Preconditioner Enhancement through Actor-critic Reinforcement Learning), a novel approach to learning matrix preconditioners. Existing preconditioners such as Jacobi, Incomplete LU, and Algebraic Multigrid methods offer problem-specific advantages but rely heavily on hyperparameter tuning. Recent advances have explored using deep neural networks to learn preconditioners, though challenges such as misbehaved objective functions and costly training procedures remain. PEARL introduces a reinforcement learning approach for learning preconditioners, specifically, a contextual bandit formulation. The framework utilizes an actor-critic model, where the actor generates the incomplete Cholesky decomposition of preconditioners, and the critic evaluates them based on reward-specific feedback. To further guide the training, we design a dual-objective function, combining updates from the critic and condition number. PEARL contributes a generalizable preconditioner learning method, dynamic sparsity exploration, and cosine schedulers for improved stability and exploratory power. We compare our approach to traditional and neural preconditioners, demonstrating improved flexibility and iterative solving speed.
Empirical Perturbation Analysis of Linear System Solvers from a Data Poisoning Perspective
Oct 01, 2024



Abstract:The perturbation analysis of linear solvers applied to systems arising broadly in machine learning settings -- for instance, when using linear regression models -- establishes an important perspective when reframing these analyses through the lens of a data poisoning attack. By analyzing solvers' responses to such attacks, this work aims to contribute to the development of more robust linear solvers and provide insights into poisoning attacks on linear solvers. In particular, we investigate how the errors in the input data will affect the fitting error and accuracy of the solution from a linear system-solving algorithm under perturbations common in adversarial attacks. We propose data perturbation through two distinct knowledge levels, developing a poisoning optimization and studying two methods of perturbation: Label-guided Perturbation (LP) and Unconditioning Perturbation (UP). Existing works mainly focus on deriving the worst-case perturbation bound from a theoretical perspective, and the analysis is often limited to specific kinds of linear system solvers. Under the circumstance that the data is intentionally perturbed -- as is the case with data poisoning -- we seek to understand how different kinds of solvers react to these perturbations, identifying those algorithms most impacted by different types of adversarial attacks.
A Dynamic Weighting Strategy to Mitigate Worker Node Failure in Distributed Deep Learning
Sep 14, 2024



Abstract:The increasing complexity of deep learning models and the demand for processing vast amounts of data make the utilization of large-scale distributed systems for efficient training essential. These systems, however, face significant challenges such as communication overhead, hardware limitations, and node failure. This paper investigates various optimization techniques in distributed deep learning, including Elastic Averaging SGD (EASGD) and the second-order method AdaHessian. We propose a dynamic weighting strategy to mitigate the problem of straggler nodes due to failure, enhancing the performance and efficiency of the overall training process. We conduct experiments with different numbers of workers and communication periods to demonstrate improved convergence rates and test performance using our strategy.
Deep Learning for Koopman Operator Estimation in Idealized Atmospheric Dynamics
Sep 10, 2024Abstract:Deep learning is revolutionizing weather forecasting, with new data-driven models achieving accuracy on par with operational physical models for medium-term predictions. However, these models often lack interpretability, making their underlying dynamics difficult to understand and explain. This paper proposes methodologies to estimate the Koopman operator, providing a linear representation of complex nonlinear dynamics to enhance the transparency of data-driven models. Despite its potential, applying the Koopman operator to large-scale problems, such as atmospheric modeling, remains challenging. This study aims to identify the limitations of existing methods, refine these models to overcome various bottlenecks, and introduce novel convolutional neural network architectures that capture simplified dynamics.
Implementing Recycling Methods for Linear Systems in Python with an Application to Multiple Objective Optimization
Feb 25, 2024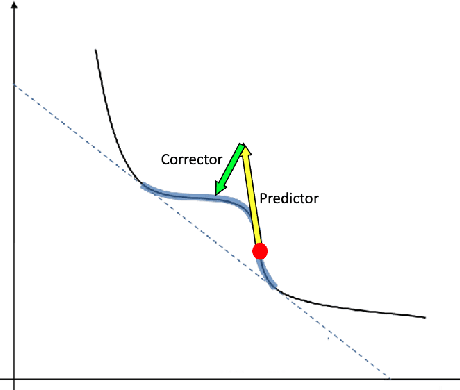
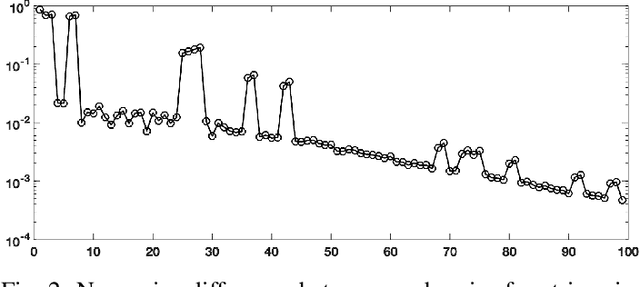
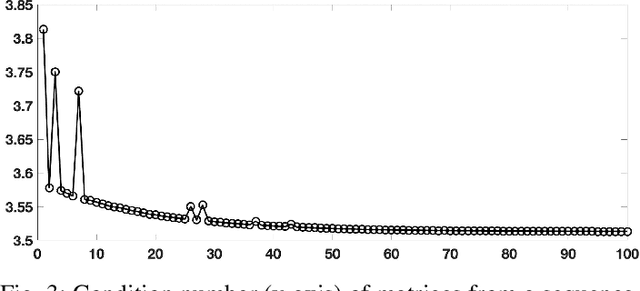
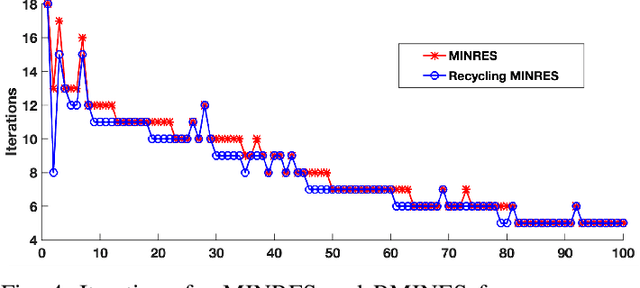
Abstract:Sequences of linear systems arise in the predictor-corrector method when computing the Pareto front for multi-objective optimization. Rather than discarding information generated when solving one system, it may be advantageous to recycle information for subsequent systems. To accomplish this, we seek to reduce the overall cost of computation when solving linear systems using common recycling methods. In this work, we assessed the performance of recycling minimum residual (RMINRES) method along with a map between coefficient matrices. For these methods to be fully integrated into the software used in Enouen et al. (2022), there must be working version of each in both Python and PyTorch. Herein, we discuss the challenges we encountered and solutions undertaken (and some ongoing) when computing efficient Python implementations of these recycling strategies. The goal of this project was to implement RMINRES in Python and PyTorch and add it to the established Pareto front code to reduce computational cost. Additionally, we wanted to implement the sparse approximate maps code in Python and PyTorch, so that it can be parallelized in future work.
Efficient first-order predictor-corrector multiple objective optimization for fair misinformation detection
Sep 15, 2022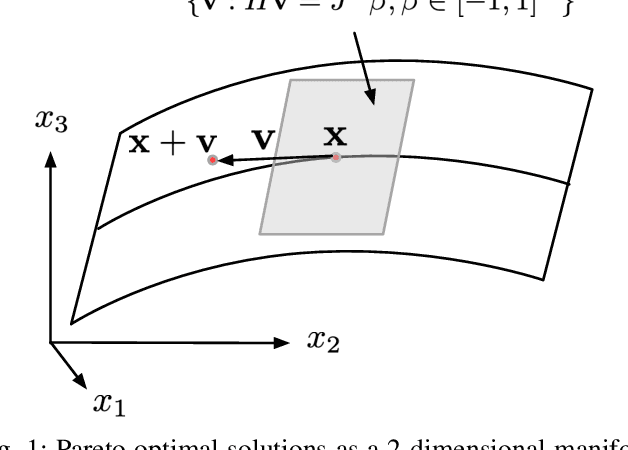
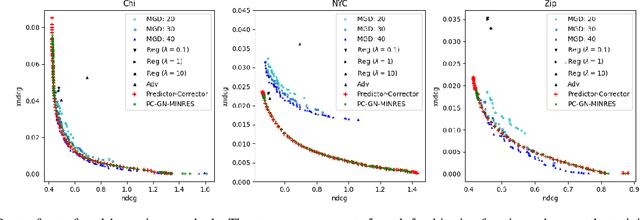
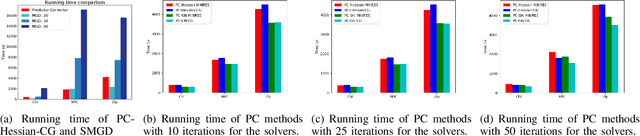
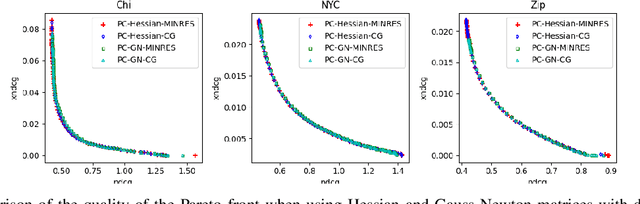
Abstract:Multiple-objective optimization (MOO) aims to simultaneously optimize multiple conflicting objectives and has found important applications in machine learning, such as minimizing classification loss and discrepancy in treating different populations for fairness. At optimality, further optimizing one objective will necessarily harm at least another objective, and decision-makers need to comprehensively explore multiple optima (called Pareto front) to pinpoint one final solution. We address the efficiency of finding the Pareto front. First, finding the front from scratch using stochastic multi-gradient descent (SMGD) is expensive with large neural networks and datasets. We propose to explore the Pareto front as a manifold from a few initial optima, based on a predictor-corrector method. Second, for each exploration step, the predictor solves a large-scale linear system that scales quadratically in the number of model parameters and requires one backpropagation to evaluate a second-order Hessian-vector product per iteration of the solver. We propose a Gauss-Newton approximation that only scales linearly, and that requires only first-order inner-product per iteration. This also allows for a choice between the MINRES and conjugate gradient methods when approximately solving the linear system. The innovations make predictor-corrector possible for large networks. Experiments on multi-objective (fairness and accuracy) misinformation detection tasks show that 1) the predictor-corrector method can find Pareto fronts better than or similar to SMGD with less time; and 2) the proposed first-order method does not harm the quality of the Pareto front identified by the second-order method, while further reduce running time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge