Density-Ratio Weighted Behavioral Cloning: Learning Control Policies from Corrupted Datasets

Offline reinforcement learning (RL) enables policy optimization from fixed datasets, making it suitable for safety-critical applications where online exploration is infeasible. However, these datasets are often contaminated by adversarial poisoning, system errors, or low-quality samples, leading to degraded policy performance in standard behavioral cloning (BC) and offline RL methods. This paper introduces Density-Ratio Weighted Behavioral Cloning (Weighted BC), a robust imitation learning approach that uses a small, verified clean reference set to estimate trajectory-level density ratios via a binary discriminator. These ratios are clipped and used as weights in the BC objective to prioritize clean expert behavior while down-weighting or discarding corrupted data, without requiring knowledge of the contamination mechanism. We establish theoretical guarantees showing convergence to the clean expert policy with finite-sample bounds that are independent of the contamination rate. A comprehensive evaluation framework is established, which incorporates various poisoning protocols (reward, state, transition, and action) on continuous control benchmarks. Experiments demonstrate that Weighted BC maintains near-optimal performance even at high contamination ratios outperforming baselines such as traditional BC, batch-constrained Q-learning (BCQ) and behavior regularized actor-critic (BRAC).

Split Conformal Prediction in the Function Space with Neural Operators

Uncertainty quantification for neural operators remains an open problem in the infinite-dimensional setting due to the lack of finite-sample coverage guarantees over functional outputs. While conformal prediction offers finite-sample guarantees in finite-dimensional spaces, it does not directly extend to function-valued outputs. Existing approaches (Gaussian processes, Bayesian neural networks, and quantile-based operators) require strong distributional assumptions or yield conservative coverage. This work extends split conformal prediction to function spaces following a two step method. We first establish finite-sample coverage guarantees in a finite-dimensional space using a discretization map in the output function space. Then these guarantees are lifted to the function-space by considering the asymptotic convergence as the discretization is refined. To characterize the effect of resolution, we decompose the conformal radius into discretization, calibration, and misspecification components. This decomposition motivates a regression-based correction to transfer calibration across resolutions. Additionally, we propose two diagnostic metrics (conformal ensemble score and internal agreement) to quantify forecast degradation in autoregressive settings. Empirical results show that our method maintains calibrated coverage with less variation under resolution shifts and achieves better coverage in super-resolution tasks.

Wasserstein Barycenter Soft Actor-Critic

Deep off-policy actor-critic algorithms have emerged as the leading framework for reinforcement learning in continuous control domains. However, most of these algorithms suffer from poor sample efficiency, especially in environments with sparse rewards. In this paper, we take a step towards addressing this issue by providing a principled directed exploration strategy. We propose Wasserstein Barycenter Soft Actor-Critic (WBSAC) algorithm, which benefits from a pessimistic actor for temporal difference learning and an optimistic actor to promote exploration. This is achieved by using the Wasserstein barycenter of the pessimistic and optimistic policies as the exploration policy and adjusting the degree of exploration throughout the learning process. We compare WBSAC with state-of-the-art off-policy actor-critic algorithms and show that WBSAC is more sample-efficient on MuJoCo continuous control tasks.

DEF: Diffusion-augmented Ensemble Forecasting

We present DEF (\textbf{\ul{D}}iffusion-augmented \textbf{\ul{E}}nsemble \textbf{\ul{F}}orecasting), a novel approach for generating initial condition perturbations. Modern approaches to initial condition perturbations are primarily designed for numerical weather prediction (NWP) solvers, limiting their applicability in the rapidly growing field of machine learning for weather prediction. Consequently, stochastic models in this domain are often developed on a case-by-case basis. We demonstrate that a simple conditional diffusion model can (1) generate meaningful structured perturbations, (2) be applied iteratively, and (3) utilize a guidance term to intuitivey control the level of perturbation. This method enables the transformation of any deterministic neural forecasting system into a stochastic one. With our stochastic extended systems, we show that the model accumulates less error over long-term forecasts while producing meaningful forecast distributions. We validate our approach on the 5.625$^\circ$ ERA5 reanalysis dataset, which comprises atmospheric and surface variables over a discretized global grid, spanning from the 1960s to the present. On this dataset, our method demonstrates improved predictive performance along with reasonable spread estimates.

Hierarchical Neuro-Symbolic Decision Transformer

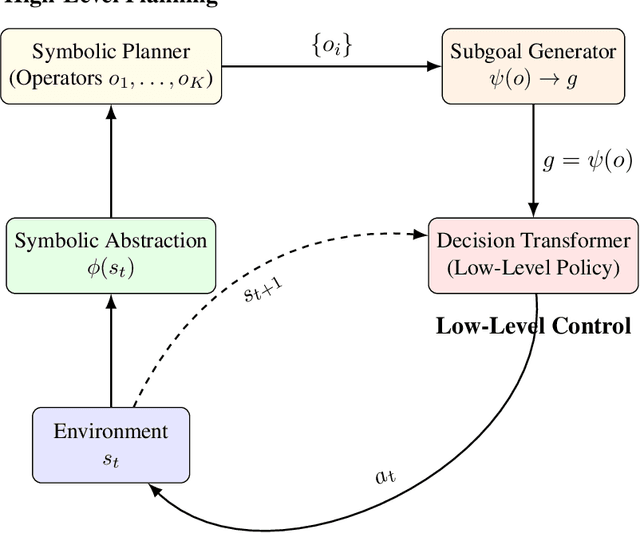
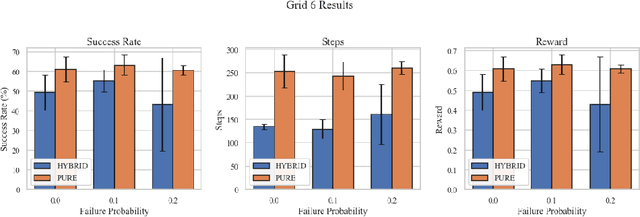
We present a hierarchical neuro-symbolic control framework that couples classical symbolic planning with transformer-based policies to address complex, long-horizon decision-making tasks. At the high level, a symbolic planner constructs an interpretable sequence of operators based on logical propositions, ensuring systematic adherence to global constraints and goals. At the low level, each symbolic operator is translated into a sub-goal token that conditions a decision transformer to generate a fine-grained sequence of actions in uncertain, high-dimensional environments. We provide theoretical analysis showing how approximation errors from both the symbolic planner and the neural execution layer accumulate. Empirical evaluations in grid-worlds with multiple keys, locked doors, and item-collection tasks show that our hierarchical approach outperforms purely end-to-end neural approach in success rates and policy efficiency.

Risk-Averse Reinforcement Learning: An Optimal Transport Perspective on Temporal Difference Learning

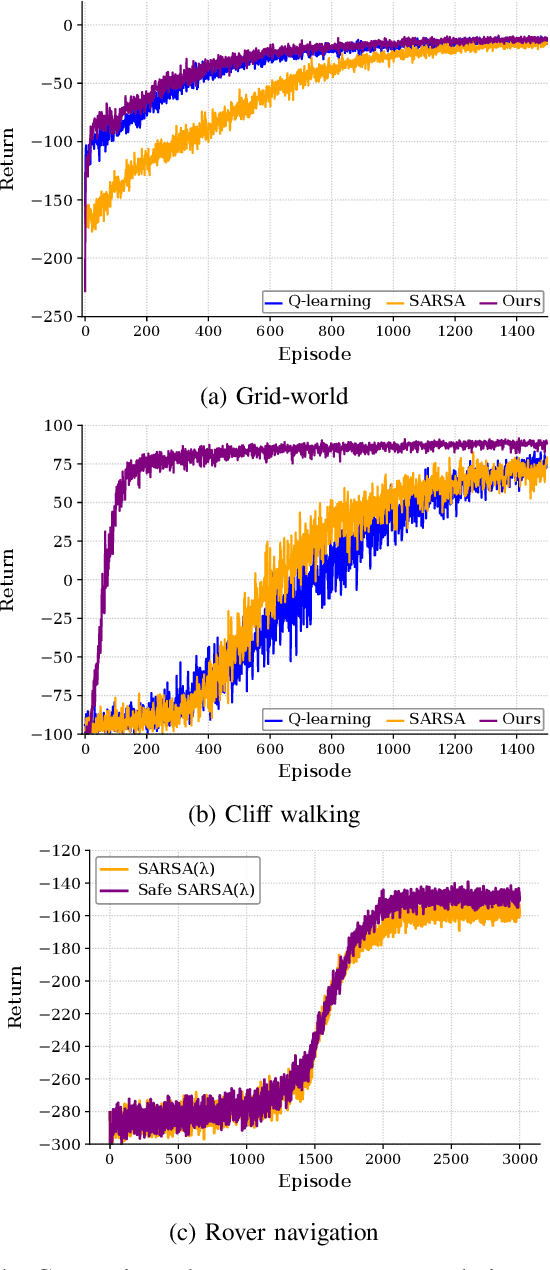
The primary goal of reinforcement learning is to develop decision-making policies that prioritize optimal performance, frequently without considering risk or safety. In contrast, safe reinforcement learning seeks to reduce or avoid unsafe states. This letter introduces a risk-averse temporal difference algorithm that uses optimal transport theory to direct the agent toward predictable behavior. By incorporating a risk indicator, the agent learns to favor actions with predictable consequences. We evaluate the proposed algorithm in several case studies and show its effectiveness in the presence of uncertainty. The results demonstrate that our method reduces the frequency of visits to risky states while preserving performance. A Python implementation of the algorithm is available at https:// github.com/SAILRIT/Risk-averse-TD-Learning.

PEARL: Preconditioner Enhancement through Actor-critic Reinforcement Learning

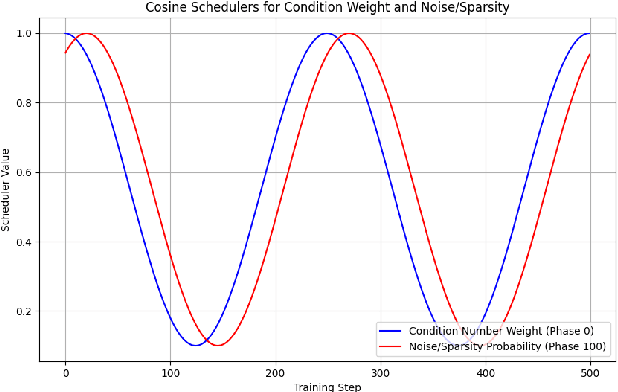
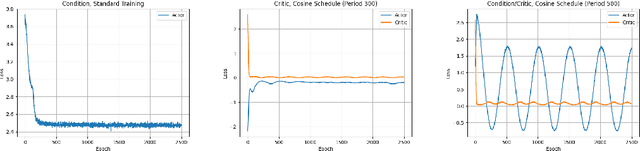
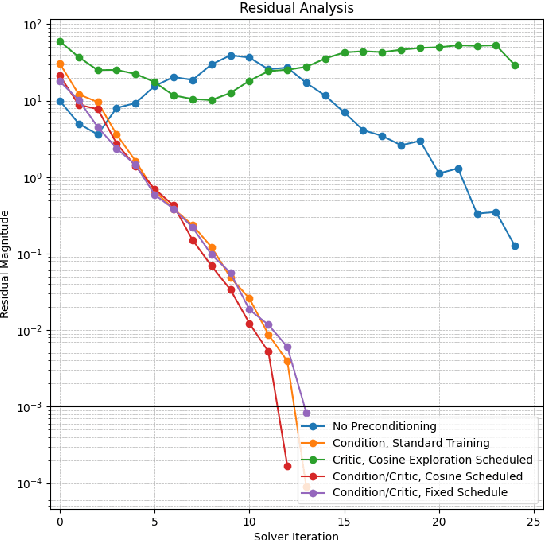
We present PEARL (Preconditioner Enhancement through Actor-critic Reinforcement Learning), a novel approach to learning matrix preconditioners. Existing preconditioners such as Jacobi, Incomplete LU, and Algebraic Multigrid methods offer problem-specific advantages but rely heavily on hyperparameter tuning. Recent advances have explored using deep neural networks to learn preconditioners, though challenges such as misbehaved objective functions and costly training procedures remain. PEARL introduces a reinforcement learning approach for learning preconditioners, specifically, a contextual bandit formulation. The framework utilizes an actor-critic model, where the actor generates the incomplete Cholesky decomposition of preconditioners, and the critic evaluates them based on reward-specific feedback. To further guide the training, we design a dual-objective function, combining updates from the critic and condition number. PEARL contributes a generalizable preconditioner learning method, dynamic sparsity exploration, and cosine schedulers for improved stability and exploratory power. We compare our approach to traditional and neural preconditioners, demonstrating improved flexibility and iterative solving speed.

Wasserstein Adaptive Value Estimation for Actor-Critic Reinforcement Learning

We present Wasserstein Adaptive Value Estimation for Actor-Critic (WAVE), an approach to enhance stability in deep reinforcement learning through adaptive Wasserstein regularization. Our method addresses the inherent instability of actor-critic algorithms by incorporating an adaptively weighted Wasserstein regularization term into the critic's loss function. We prove that WAVE achieves $\mathcal{O}\left(\frac{1}{k}\right)$ convergence rate for the critic's mean squared error and provide theoretical guarantees for stability through Wasserstein-based regularization. Using the Sinkhorn approximation for computational efficiency, our approach automatically adjusts the regularization based on the agent's performance. Theoretical analysis and experimental results demonstrate that WAVE achieves superior performance compared to standard actor-critic methods.

Hierarchical Upper Confidence Bounds for Constrained Online Learning

The multi-armed bandit (MAB) problem is a foundational framework in sequential decision-making under uncertainty, extensively studied for its applications in areas such as clinical trials, online advertising, and resource allocation. Traditional MAB formulations, however, do not adequately capture scenarios where decisions are structured hierarchically, involve multi-level constraints, or feature context-dependent action spaces. In this paper, we introduce the hierarchical constrained bandits (HCB) framework, which extends the contextual bandit problem to incorporate hierarchical decision structures and multi-level constraints. We propose the hierarchical constrained upper confidence bound (HC-UCB) algorithm, designed to address the complexities of the HCB problem by leveraging confidence bounds within a hierarchical setting. Our theoretical analysis establishes sublinear regret bounds for HC-UCB and provides high-probability guarantees for constraint satisfaction at all hierarchical levels. Furthermore, we derive a minimax lower bound on the regret for the HCB problem, demonstrating the near-optimality of our algorithm. The results are significant for real-world applications where decision-making processes are inherently hierarchical and constrained, offering a robust and efficient solution that balances exploration and exploitation across multiple levels of decision-making.

Optimizing Falsification for Learning-Based Control Systems: A Multi-Fidelity Bayesian Approach

Testing controllers in safety-critical systems is vital for ensuring their safety and preventing failures. In this paper, we address the falsification problem within learning-based closed-loop control systems through simulation. This problem involves the identification of counterexamples that violate system safety requirements and can be formulated as an optimization task based on these requirements. Using full-fidelity simulator data in this optimization problem can be computationally expensive. To improve efficiency, we propose a multi-fidelity Bayesian optimization falsification framework that harnesses simulators with varying levels of accuracy. Our proposed framework can transition between different simulators and establish meaningful relationships between them. Through multi-fidelity Bayesian optimization, we determine both the optimal system input likely to be a counterexample and the appropriate fidelity level for assessment. We evaluated our approach across various Gym environments, each featuring different levels of fidelity. Our experiments demonstrate that multi-fidelity Bayesian optimization is more computationally efficient than full-fidelity Bayesian optimization and other baseline methods in detecting counterexamples. A Python implementation of the algorithm is available at https://github.com/SAILRIT/MFBO_Falsification.