Fully invertible hyperbolic neural networks for segmenting large-scale surface and sub-surface data

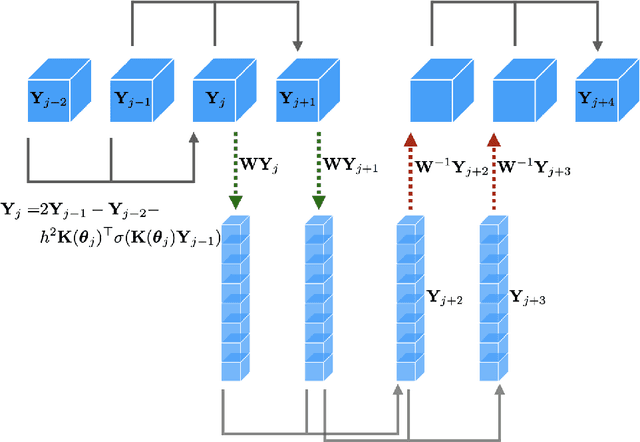
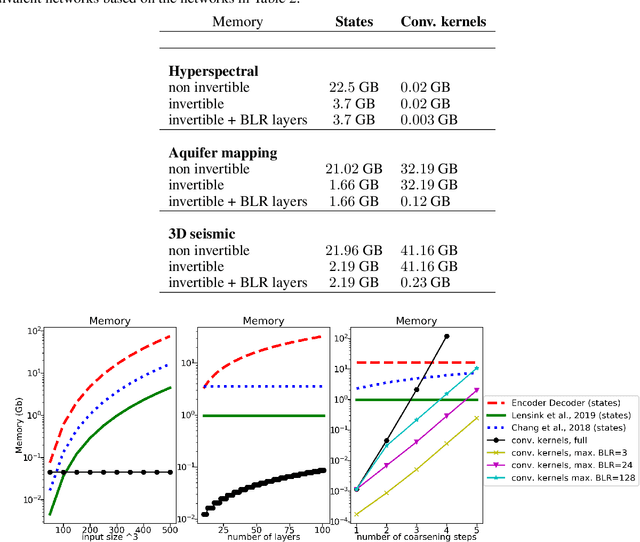
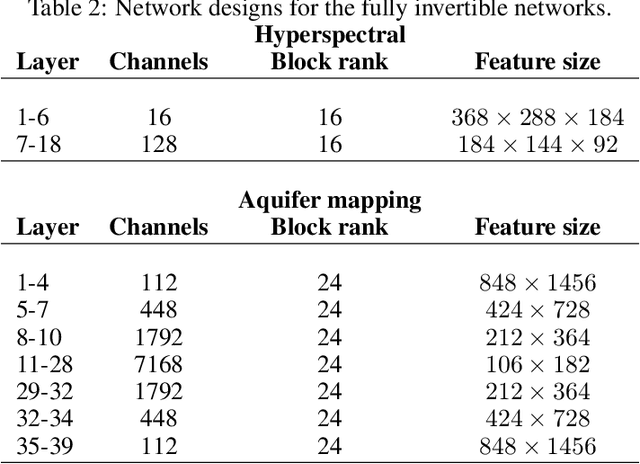
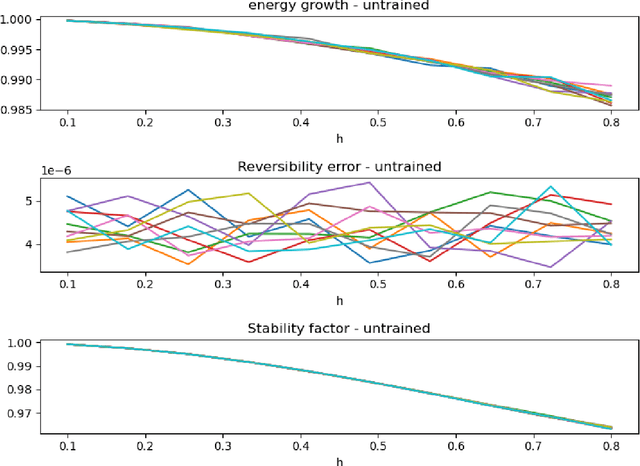
The large spatial/temporal/frequency scale of geoscience and remote-sensing datasets causes memory issues when using convolutional neural networks for (sub-) surface data segmentation. Recently developed fully reversible or fully invertible networks can mostly avoid memory limitations by recomputing the states during the backward pass through the network. This results in a low and fixed memory requirement for storing network states, as opposed to the typical linear memory growth with network depth. This work focuses on a fully invertible network based on the telegraph equation. While reversibility saves the major amount of memory used in deep networks by the data, the convolutional kernels can take up most memory if fully invertible networks contain multiple invertible pooling/coarsening layers. We address the explosion of the number of convolutional kernels by combining fully invertible networks with layers that contain the convolutional kernels in a compressed form directly. A second challenge is that invertible networks output a tensor the same size as its input. This property prevents the straightforward application of invertible networks to applications that map between different input-output dimensions, need to map to outputs with more channels than present in the input data, or desire outputs that decrease/increase the resolution compared to the input data. However, we show that by employing invertible networks in a non-standard fashion, we can still use them for these tasks. Examples in hyperspectral land-use classification, airborne geophysical surveying, and seismic imaging illustrate that we can input large data volumes in one chunk and do not need to work on small patches, use dimensionality reduction, or employ methods that classify a patch to a single central pixel.

Paired Autoencoders for Inverse Problems

We consider the solution of nonlinear inverse problems where the forward problem is a discretization of a partial differential equation. Such problems are notoriously difficult to solve in practice and require minimizing a combination of a data-fit term and a regularization term. The main computational bottleneck of typical algorithms is the direct estimation of the data misfit. Therefore, likelihood-free approaches have become appealing alternatives. Nonetheless, difficulties in generalization and limitations in accuracy have hindered their broader utility and applicability. In this work, we use a paired autoencoder framework as a likelihood-free estimator for inverse problems. We show that the use of such an architecture allows us to construct a solution efficiently and to overcome some known open problems when using likelihood-free estimators. In particular, our framework can assess the quality of the solution and improve on it if needed. We demonstrate the viability of our approach using examples from full waveform inversion and inverse electromagnetic imaging.

InvertibleNetworks.jl: A Julia package for scalable normalizing flows

InvertibleNetworks.jl is a Julia package designed for the scalable implementation of normalizing flows, a method for density estimation and sampling in high-dimensional distributions. This package excels in memory efficiency by leveraging the inherent invertibility of normalizing flows, which significantly reduces memory requirements during backpropagation compared to existing normalizing flow packages that rely on automatic differentiation frameworks. InvertibleNetworks.jl has been adapted for diverse applications, including seismic imaging, medical imaging, and CO2 monitoring, demonstrating its effectiveness in learning high-dimensional distributions.

CQnet: convex-geometric interpretation and constraining neural-network trajectories

We introduce CQnet, a neural network with origins in the CQ algorithm for solving convex split-feasibility problems and forward-backward splitting. CQnet's trajectories are interpretable as particles that are tracking a changing constraint set via its point-to-set distance function while being elements of another constraint set at every layer. More than just a convex-geometric interpretation, CQnet accommodates learned and deterministic constraints that may be sample or data-specific and are satisfied by every layer and the output. Furthermore, the states in CQnet progress toward another constraint set at every layer. We provide proof of stability/nonexpansiveness with minimal assumptions. The combination of constraint handling and stability put forward CQnet as a candidate for various tasks where prior knowledge exists on the network states or output.

Point-to-set distance functions for weakly supervised segmentation

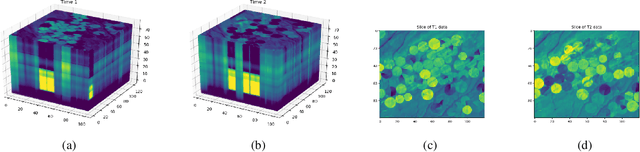
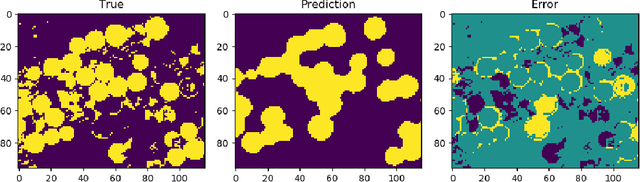
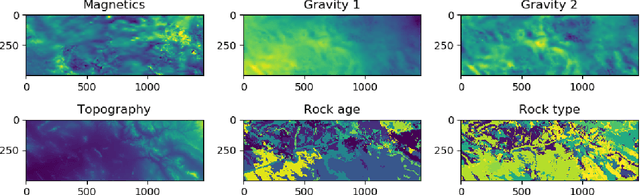
When pixel-level masks or partial annotations are not available for training neural networks for semantic segmentation, it is possible to use higher-level information in the form of bounding boxes, or image tags. In the imaging sciences, many applications do not have an object-background structure and bounding boxes are not available. Any available annotation typically comes from ground truth or domain experts. A direct way to train without masks is using prior knowledge on the size of objects/classes in the segmentation. We present a new algorithm to include such information via constraints on the network output, implemented via projection-based point-to-set distance functions. This type of distance functions always has the same functional form of the derivative, and avoids the need to adapt penalty functions to different constraints, as well as issues related to constraining properties typically associated with non-differentiable functions. Whereas object size information is known to enable object segmentation from bounding boxes from datasets with many general and medical images, we show that the applications extend to the imaging sciences where data represents indirect measurements, even in the case of single examples. We illustrate the capabilities in case of a) one or more classes do not have any annotation; b) there is no annotation at all; c) there are bounding boxes. We use data for hyperspectral time-lapse imaging, object segmentation in corrupted images, and sub-surface aquifer mapping from airborne-geophysical remote-sensing data. The examples verify that the developed methodology alleviates difficulties with annotating non-visual imagery for a range of experimental settings.

Deep connections between learning from limited labels & physical parameter estimation -- inspiration for regularization

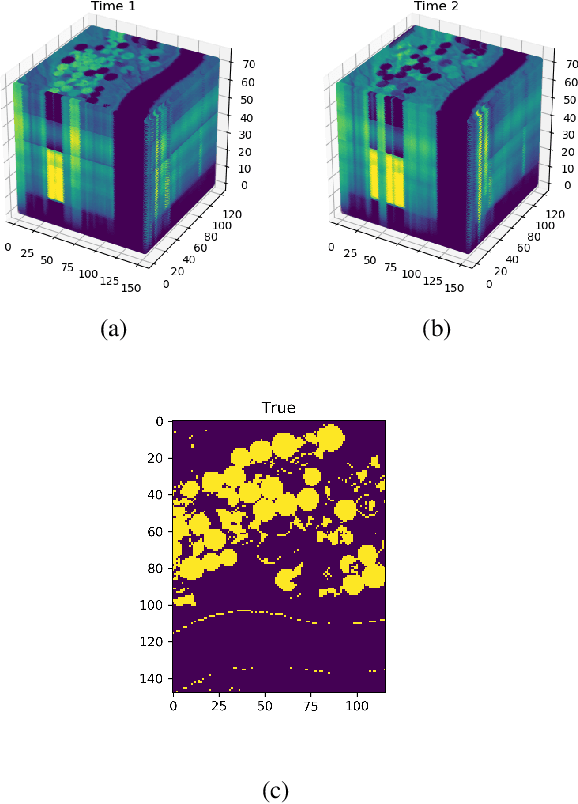
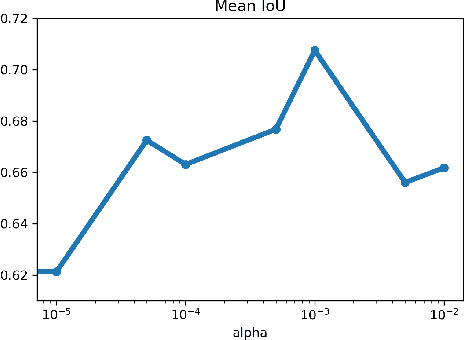
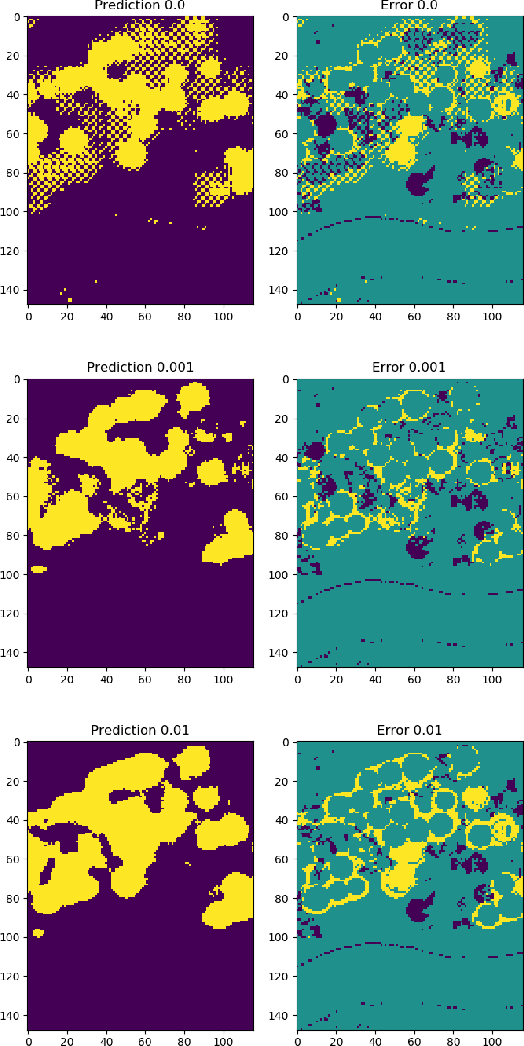
Recently established equivalences between differential equations and the structure of neural networks enabled some interpretation of training of a neural network as partial-differential-equation (PDE) constrained optimization. We add to the previously established connections, explicit regularization that is particularly beneficial in the case of single large-scale examples with partial annotation. We show that explicit regularization of model parameters in PDE constrained optimization translates to regularization of the network output. Examination of the structure of the corresponding Lagrangian and backpropagation algorithm do not reveal additional computational challenges. A hyperspectral imaging example shows that minimum prior information together with cross-validation for optimal regularization parameters boosts the segmentation accuracy.

Fully reversible neural networks for large-scale surface and sub-surface characterization via remote sensing

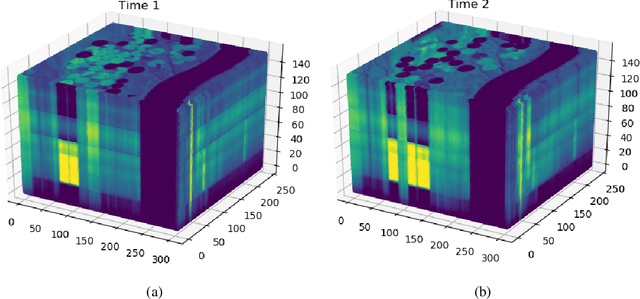
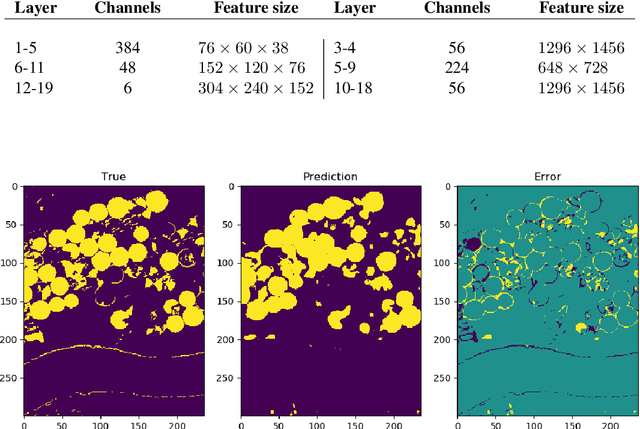
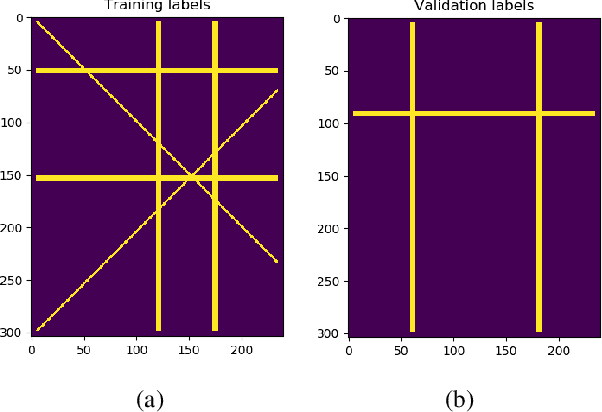
The large spatial/frequency scale of hyperspectral and airborne magnetic and gravitational data causes memory issues when using convolutional neural networks for (sub-) surface characterization. Recently developed fully reversible networks can mostly avoid memory limitations by virtue of having a low and fixed memory requirement for storing network states, as opposed to the typical linear memory growth with depth. Fully reversible networks enable the training of deep neural networks that take in entire data volumes, and create semantic segmentations in one go. This approach avoids the need to work in small patches or map a data patch to the class of just the central pixel. The cross-entropy loss function requires small modifications to work in conjunction with a fully reversible network and learn from sparsely sampled labels without ever seeing fully labeled ground truth. We show examples from land-use change detection from hyperspectral time-lapse data, and regional aquifer mapping from airborne geophysical and geological data.

Symmetric block-low-rank layers for fully reversible multilevel neural networks

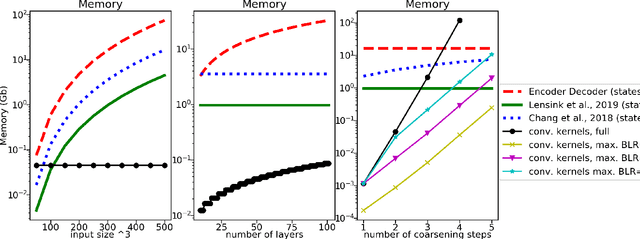
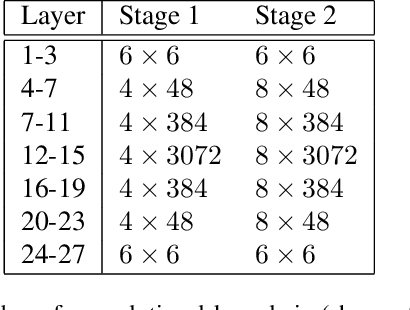
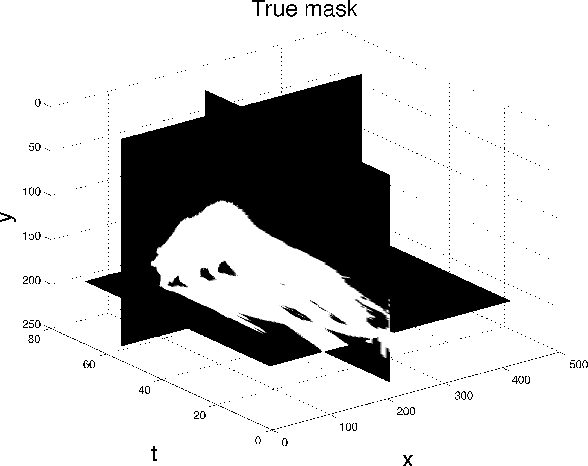
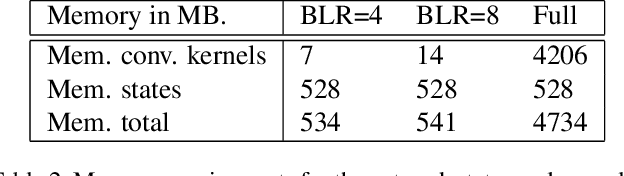
Factors that limit the size of the input and output of a neural network include memory requirements for the network states/activations to compute gradients, as well as memory for the convolutional kernels or other weights. The memory restriction is especially limiting for applications where we want to learn how to map volumetric data to the desired output, such as video-to-video. Recently developed fully reversible neural networks enable gradient computations using storage of the network states for a couple of layers only. While this saves a tremendous amount of memory, it is the convolutional kernels that take up most memory if fully reversible networks contain multiple invertible pooling/coarsening layers. Invertible coarsening operators such as the orthogonal wavelet transform cause the number of channels to grow explosively. We address this issue by combining fully reversible networks with layers that contain the convolutional kernels in a compressed form directly. Specifically, we introduce a layer that has a symmetric block-low-rank structure. In spirit, this layer is similar to bottleneck and squeeze-and-expand structures. We contribute symmetry by construction, and a combination of notation and flattening of tensors allows us to interpret these network structures in linear algebraic fashion as a block-low-rank matrix in factorized form and observe various properties. A video segmentation example shows that we can train a network to segment the entire video in one go, which would not be possible, in terms of memory requirements, using non-reversible networks and previously proposed reversible networks.

Fully Hyperbolic Convolutional Neural Networks

Convolutional Neural Networks (CNN) have recently seen tremendous success in various computer vision tasks. However, their application to problems with high dimensional input and output has been limited by two factors. First, in the training stage, it is necessary to store network activations for back propagation. Second, in the inference stage, a few copies of the image are typically stored to be concatenated to other network states deeper in the network. In these settings, the memory requirements associated with storing activations can exceed what is feasible with current hardware. For the problem of image classification, reversible architectures have been proposed that allow one to recalculate activations in the backwards pass instead of storing them, however, such networks do not perform well for problems such as segmentation. Furthermore, currently only block reversible networks have been possible because pooling operations are not reversible. Motivated by the propagation of signals over physical networks, that are governed by the hyperbolic Telegraph equation, in this work we introduce a fully conservative hyperbolic network for problems with high dimensional input and output. We introduce a coarsening operation that allows completely reversible CNNs by using the Discrete Wavelet Transform and its inverse to both coarsen and interpolate the network state and change the number of channels. This means that during training we do not need to store the activations from the forward pass, and can train arbitrarily deep or wide networks. Furthermore, our network has a much lower memory footprint for inference. We show that we are able to achieve results comparable to the state of the art in image classification, depth estimation, and semantic segmentation, with a much lower memory footprint.

Neural-networks for geophysicists and their application to seismic data interpretation

Neural-networks have seen a surge of interest for the interpretation of seismic images during the last few years. Network-based learning methods can provide fast and accurate automatic interpretation, provided there are sufficiently many training labels. We provide an introduction to the field aimed at geophysicists that are familiar with the framework of forward modeling and inversion. We explain the similarities and differences between deep networks to other geophysical inverse problems and show their utility in solving problems such as lithology interpolation between wells, horizon tracking and segmentation of seismic images. The benefits of our approach are demonstrated on field data from the Sea of Ireland and the North Sea.