Paired Wasserstein Autoencoders for Conditional Sampling

Wasserstein distances greatly influenced and coined various types of generative neural network models. Wasserstein autoencoders are particularly notable for their mathematical simplicity and straight-forward implementation. However, their adaptation to the conditional case displays theoretical difficulties. As a remedy, we propose the use of two paired autoencoders. Under the assumption of an optimal autoencoder pair, we leverage the pairwise independence condition of our prescribed Gaussian latent distribution to overcome this theoretical hurdle. We conduct several experiments to showcase the practical applicability of the resulting paired Wasserstein autoencoders. Here, we consider imaging tasks and enable conditional sampling for denoising, inpainting, and unsupervised image translation. Moreover, we connect our image translation model to the Monge map behind Wasserstein-2 distances.

Sparse $L^1$-Autoencoders for Scientific Data Compression

Scientific datasets present unique challenges for machine learning-driven compression methods, including more stringent requirements on accuracy and mitigation of potential invalidating artifacts. Drawing on results from compressed sensing and rate-distortion theory, we introduce effective data compression methods by developing autoencoders using high dimensional latent spaces that are $L^1$-regularized to obtain sparse low dimensional representations. We show how these information-rich latent spaces can be used to mitigate blurring and other artifacts to obtain highly effective data compression methods for scientific data. We demonstrate our methods for short angle scattering (SAS) datasets showing they can achieve compression ratios around two orders of magnitude and in some cases better. Our compression methods show promise for use in addressing current bottlenecks in transmission, storage, and analysis in high-performance distributed computing environments. This is central to processing the large volume of SAS data being generated at shared experimental facilities around the world to support scientific investigations. Our approaches provide general ways for obtaining specialized compression methods for targeted scientific datasets.

Paired Autoencoders for Inverse Problems

We consider the solution of nonlinear inverse problems where the forward problem is a discretization of a partial differential equation. Such problems are notoriously difficult to solve in practice and require minimizing a combination of a data-fit term and a regularization term. The main computational bottleneck of typical algorithms is the direct estimation of the data misfit. Therefore, likelihood-free approaches have become appealing alternatives. Nonetheless, difficulties in generalization and limitations in accuracy have hindered their broader utility and applicability. In this work, we use a paired autoencoder framework as a likelihood-free estimator for inverse problems. We show that the use of such an architecture allows us to construct a solution efficiently and to overcome some known open problems when using likelihood-free estimators. In particular, our framework can assess the quality of the solution and improve on it if needed. We demonstrate the viability of our approach using examples from full waveform inversion and inverse electromagnetic imaging.

Goal-oriented Uncertainty Quantification for Inverse Problems via Variational Encoder-Decoder Networks

In this work, we describe a new approach that uses variational encoder-decoder (VED) networks for efficient goal-oriented uncertainty quantification for inverse problems. Contrary to standard inverse problems, these approaches are \emph{goal-oriented} in that the goal is to estimate some quantities of interest (QoI) that are functions of the solution of an inverse problem, rather than the solution itself. Moreover, we are interested in computing uncertainty metrics associated with the QoI, thus utilizing a Bayesian approach for inverse problems that incorporates the prediction operator and techniques for exploring the posterior. This may be particularly challenging, especially for nonlinear, possibly unknown, operators and nonstandard prior assumptions. We harness recent advances in machine learning, i.e., VED networks, to describe a data-driven approach to large-scale inverse problems. This enables a real-time goal-oriented uncertainty quantification for the QoI. One of the advantages of our approach is that we avoid the need to solve challenging inversion problems by training a network to approximate the mapping from observations to QoI. Another main benefit is that we enable uncertainty quantification for the QoI by leveraging probability distributions in the latent space. This allows us to efficiently generate QoI samples and circumvent complicated or even unknown forward models and prediction operators. Numerical results from medical tomography reconstruction and nonlinear hydraulic tomography demonstrate the potential and broad applicability of the approach.

slimTrain -- A Stochastic Approximation Method for Training Separable Deep Neural Networks

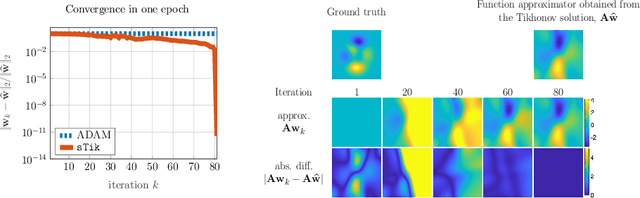
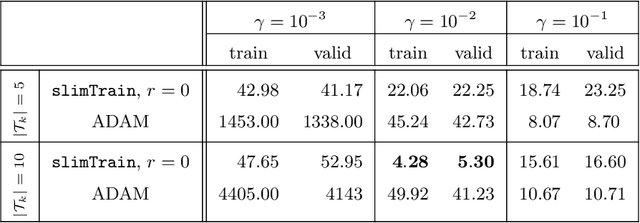
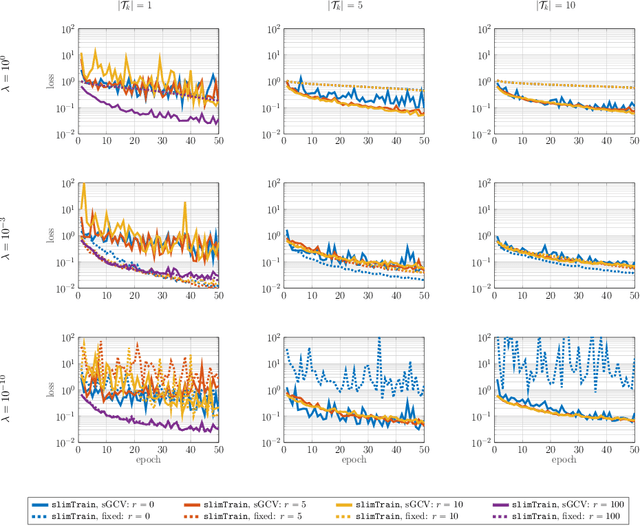
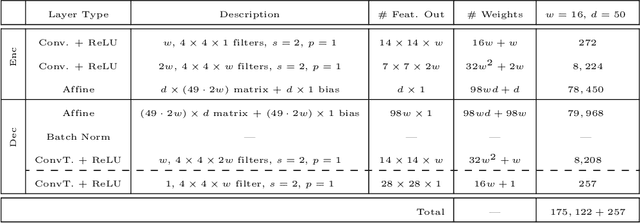
Deep neural networks (DNNs) have shown their success as high-dimensional function approximators in many applications; however, training DNNs can be challenging in general. DNN training is commonly phrased as a stochastic optimization problem whose challenges include non-convexity, non-smoothness, insufficient regularization, and complicated data distributions. Hence, the performance of DNNs on a given task depends crucially on tuning hyperparameters, especially learning rates and regularization parameters. In the absence of theoretical guidelines or prior experience on similar tasks, this requires solving many training problems, which can be time-consuming and demanding on computational resources. This can limit the applicability of DNNs to problems with non-standard, complex, and scarce datasets, e.g., those arising in many scientific applications. To remedy the challenges of DNN training, we propose slimTrain, a stochastic optimization method for training DNNs with reduced sensitivity to the choice hyperparameters and fast initial convergence. The central idea of slimTrain is to exploit the separability inherent in many DNN architectures; that is, we separate the DNN into a nonlinear feature extractor followed by a linear model. This separability allows us to leverage recent advances made for solving large-scale, linear, ill-posed inverse problems. Crucially, for the linear weights, slimTrain does not require a learning rate and automatically adapts the regularization parameter. Since our method operates on mini-batches, its computational overhead per iteration is modest. In our numerical experiments, slimTrain outperforms existing DNN training methods with the recommended hyperparameter settings and reduces the sensitivity of DNN training to the remaining hyperparameters.

Learning Regularization Parameters of Inverse Problems via Deep Neural Networks

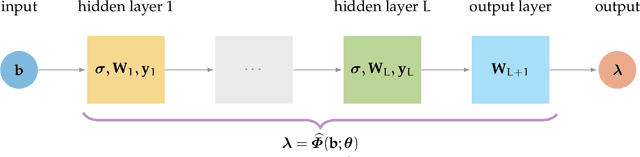
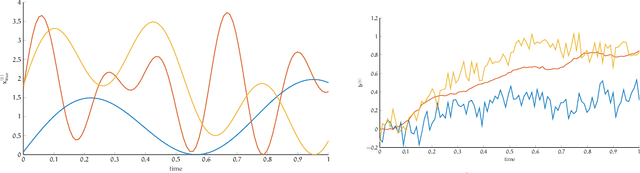
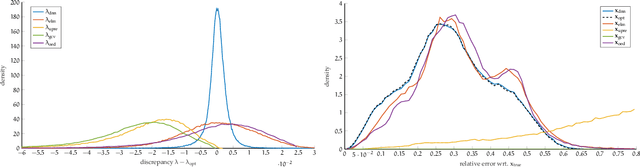
In this work, we describe a new approach that uses deep neural networks (DNN) to obtain regularization parameters for solving inverse problems. We consider a supervised learning approach, where a network is trained to approximate the mapping from observation data to regularization parameters. Once the network is trained, regularization parameters for newly obtained data can be computed by efficient forward propagation of the DNN. We show that a wide variety of regularization functionals, forward models, and noise models may be considered. The network-obtained regularization parameters can be computed more efficiently and may even lead to more accurate solutions compared to existing regularization parameter selection methods. We emphasize that the key advantage of using DNNs for learning regularization parameters, compared to previous works on learning via optimal experimental design or empirical Bayes risk minimization, is greater generalizability. That is, rather than computing one set of parameters that is optimal with respect to one particular design objective, DNN-computed regularization parameters are tailored to the specific features or properties of the newly observed data. Thus, our approach may better handle cases where the observation is not a close representation of the training set. Furthermore, we avoid the need for expensive and challenging bilevel optimization methods as utilized in other existing training approaches. Numerical results demonstrate the potential of using DNNs to learn regularization parameters.

Stochastic Newton and Quasi-Newton Methods for Large Linear Least-squares Problems

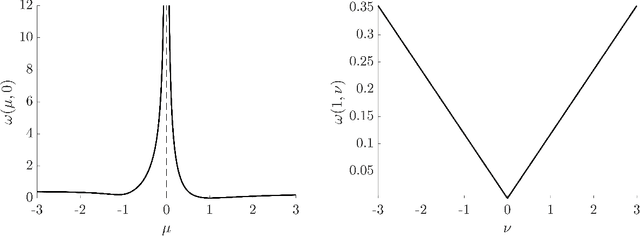
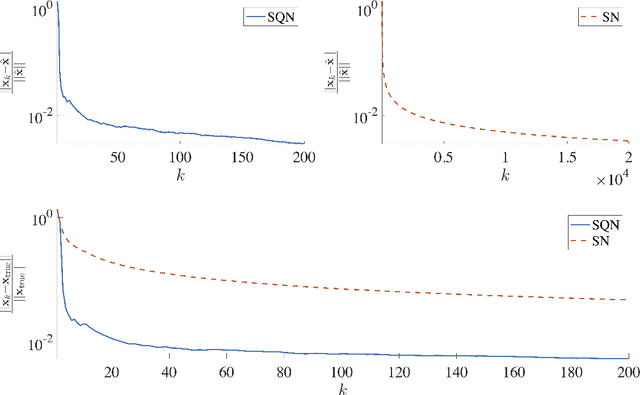
We describe stochastic Newton and stochastic quasi-Newton approaches to efficiently solve large linear least-squares problems where the very large data sets present a significant computational burden (e.g., the size may exceed computer memory or data are collected in real-time). In our proposed framework, stochasticity is introduced in two different frameworks as a means to overcome these computational limitations, and probability distributions that can exploit structure and/or sparsity are considered. Theoretical results on consistency of the approximations for both the stochastic Newton and the stochastic quasi-Newton methods are provided. The results show, in particular, that stochastic Newton iterates, in contrast to stochastic quasi-Newton iterates, may not converge to the desired least-squares solution. Numerical examples, including an example from extreme learning machines, demonstrate the potential applications of these methods.