Goal-oriented Uncertainty Quantification for Inverse Problems via Variational Encoder-Decoder Networks

In this work, we describe a new approach that uses variational encoder-decoder (VED) networks for efficient goal-oriented uncertainty quantification for inverse problems. Contrary to standard inverse problems, these approaches are \emph{goal-oriented} in that the goal is to estimate some quantities of interest (QoI) that are functions of the solution of an inverse problem, rather than the solution itself. Moreover, we are interested in computing uncertainty metrics associated with the QoI, thus utilizing a Bayesian approach for inverse problems that incorporates the prediction operator and techniques for exploring the posterior. This may be particularly challenging, especially for nonlinear, possibly unknown, operators and nonstandard prior assumptions. We harness recent advances in machine learning, i.e., VED networks, to describe a data-driven approach to large-scale inverse problems. This enables a real-time goal-oriented uncertainty quantification for the QoI. One of the advantages of our approach is that we avoid the need to solve challenging inversion problems by training a network to approximate the mapping from observations to QoI. Another main benefit is that we enable uncertainty quantification for the QoI by leveraging probability distributions in the latent space. This allows us to efficiently generate QoI samples and circumvent complicated or even unknown forward models and prediction operators. Numerical results from medical tomography reconstruction and nonlinear hydraulic tomography demonstrate the potential and broad applicability of the approach.

Learning Regularization Parameters of Inverse Problems via Deep Neural Networks

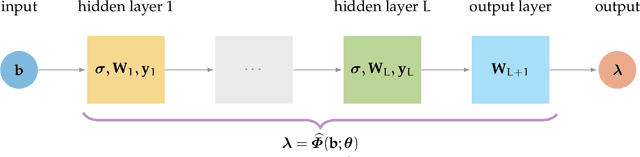
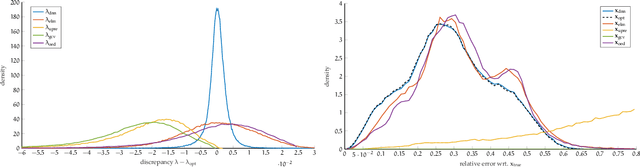
In this work, we describe a new approach that uses deep neural networks (DNN) to obtain regularization parameters for solving inverse problems. We consider a supervised learning approach, where a network is trained to approximate the mapping from observation data to regularization parameters. Once the network is trained, regularization parameters for newly obtained data can be computed by efficient forward propagation of the DNN. We show that a wide variety of regularization functionals, forward models, and noise models may be considered. The network-obtained regularization parameters can be computed more efficiently and may even lead to more accurate solutions compared to existing regularization parameter selection methods. We emphasize that the key advantage of using DNNs for learning regularization parameters, compared to previous works on learning via optimal experimental design or empirical Bayes risk minimization, is greater generalizability. That is, rather than computing one set of parameters that is optimal with respect to one particular design objective, DNN-computed regularization parameters are tailored to the specific features or properties of the newly observed data. Thus, our approach may better handle cases where the observation is not a close representation of the training set. Furthermore, we avoid the need for expensive and challenging bilevel optimization methods as utilized in other existing training approaches. Numerical results demonstrate the potential of using DNNs to learn regularization parameters.