Slicing the Gaussian Mixture Wasserstein Distance

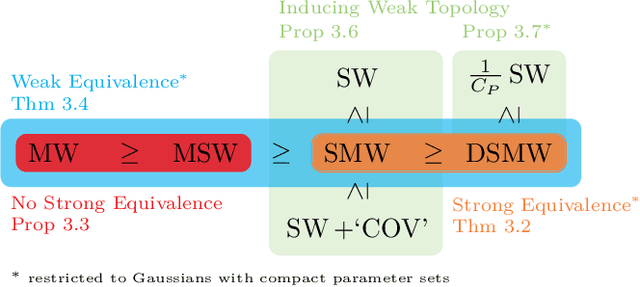
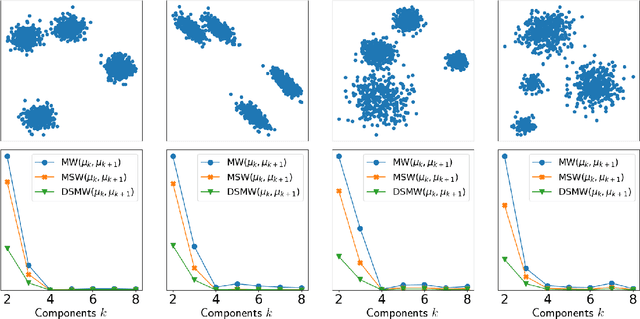
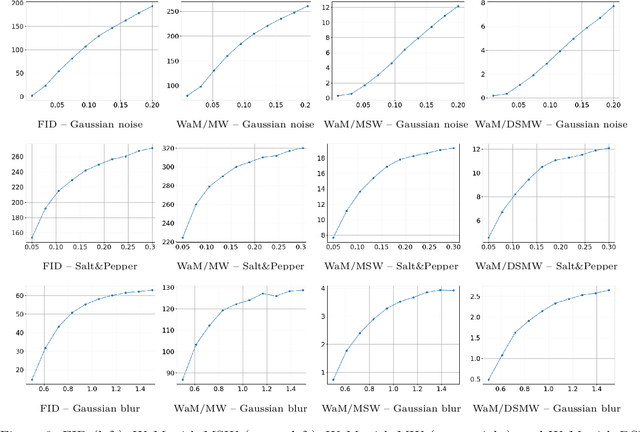
Gaussian mixture models (GMMs) are widely used in machine learning for tasks such as clustering, classification, image reconstruction, and generative modeling. A key challenge in working with GMMs is defining a computationally efficient and geometrically meaningful metric. The mixture Wasserstein (MW) distance adapts the Wasserstein metric to GMMs and has been applied in various domains, including domain adaptation, dataset comparison, and reinforcement learning. However, its high computational cost -- arising from repeated Wasserstein distance computations involving matrix square root estimations and an expensive linear program -- limits its scalability to high-dimensional and large-scale problems. To address this, we propose multiple novel slicing-based approximations to the MW distance that significantly reduce computational complexity while preserving key optimal transport properties. From a theoretical viewpoint, we establish several weak and strong equivalences between the introduced metrics, and show the relations to the original MW distance and the well-established sliced Wasserstein distance. Furthermore, we validate the effectiveness of our approach through numerical experiments, demonstrating computational efficiency and applications in clustering, perceptual image comparison, and GMM minimization

Joint Metric Space Embedding by Unbalanced OT with Gromov-Wasserstein Marginal Penalization

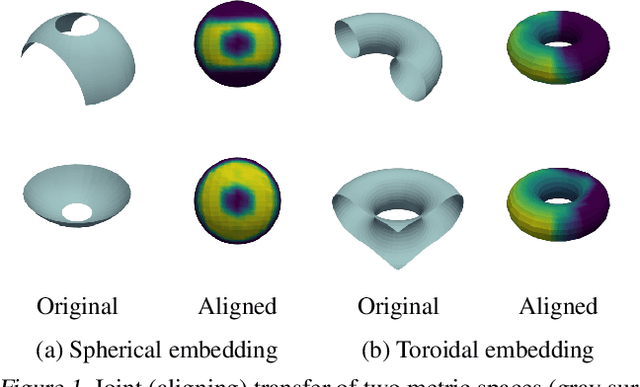
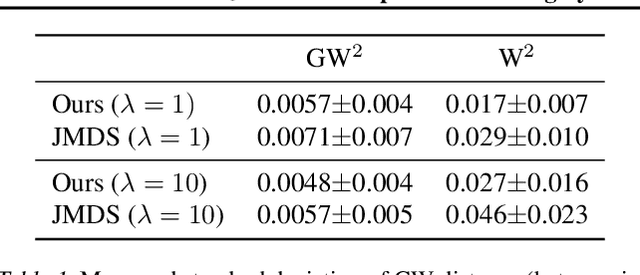
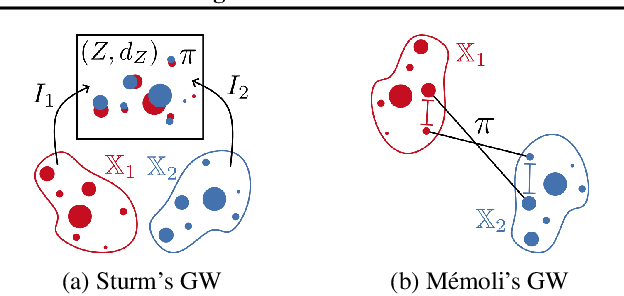
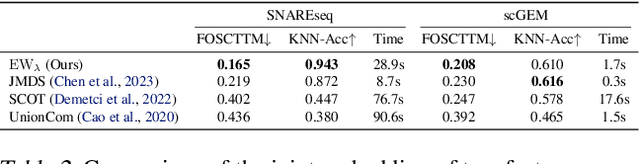
We propose a new approach for unsupervised alignment of heterogeneous datasets, which maps data from two different domains without any known correspondences to a common metric space. Our method is based on an unbalanced optimal transport problem with Gromov-Wasserstein marginal penalization. It can be seen as a counterpart to the recently introduced joint multidimensional scaling method. We prove that there exists a minimizer of our functional and that for penalization parameters going to infinity, the corresponding sequence of minimizers converges to a minimizer of the so-called embedded Wasserstein distance. Our model can be reformulated as a quadratic, multi-marginal, unbalanced optimal transport problem, for which a bi-convex relaxation admits a numerical solver via block-coordinate descent. We provide numerical examples for joint embeddings in Euclidean as well as non-Euclidean spaces.

Paired Wasserstein Autoencoders for Conditional Sampling

Wasserstein distances greatly influenced and coined various types of generative neural network models. Wasserstein autoencoders are particularly notable for their mathematical simplicity and straight-forward implementation. However, their adaptation to the conditional case displays theoretical difficulties. As a remedy, we propose the use of two paired autoencoders. Under the assumption of an optimal autoencoder pair, we leverage the pairwise independence condition of our prescribed Gaussian latent distribution to overcome this theoretical hurdle. We conduct several experiments to showcase the practical applicability of the resulting paired Wasserstein autoencoders. Here, we consider imaging tasks and enable conditional sampling for denoising, inpainting, and unsupervised image translation. Moreover, we connect our image translation model to the Monge map behind Wasserstein-2 distances.

Conditional Generative Models for Contrast-Enhanced Synthesis of T1w and T1 Maps in Brain MRI

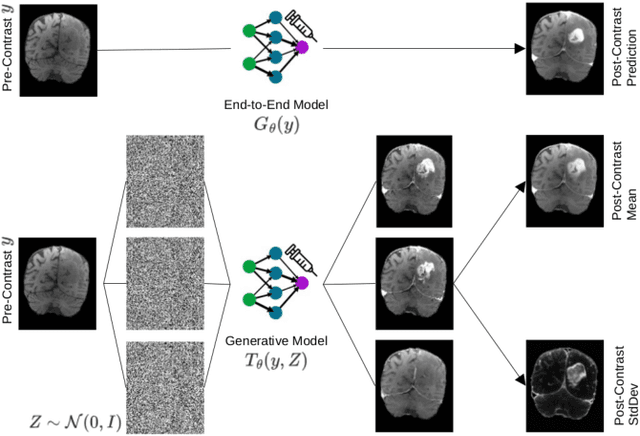
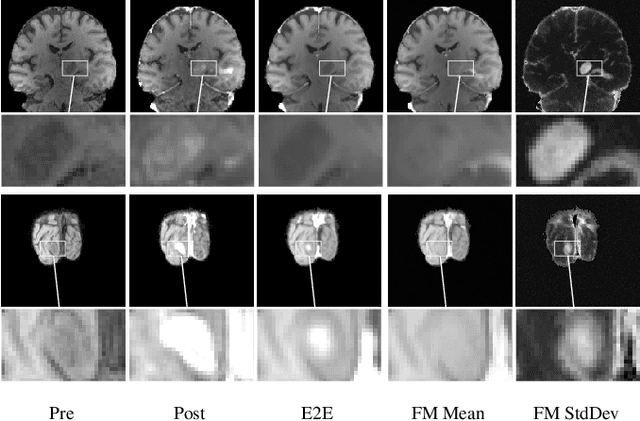
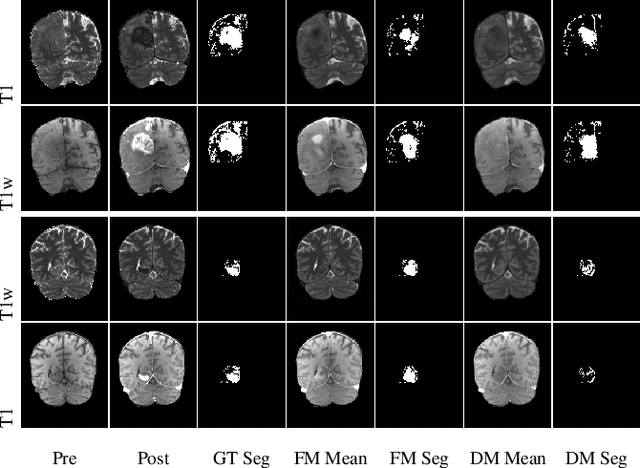
Contrast enhancement by Gadolinium-based contrast agents (GBCAs) is a vital tool for tumor diagnosis in neuroradiology. Based on brain MRI scans of glioblastoma before and after Gadolinium administration, we address enhancement prediction by neural networks with two new contributions. Firstly, we study the potential of generative models, more precisely conditional diffusion and flow matching, for uncertainty quantification in virtual enhancement. Secondly, we examine the performance of T1 scans from quantitive MRI versus T1-weighted scans. In contrast to T1-weighted scans, these scans have the advantage of a physically meaningful and thereby comparable voxel range. To compare network prediction performance of these two modalities with incompatible gray-value scales, we propose to evaluate segmentations of contrast-enhanced regions of interest using Dice and Jaccard scores. Across models, we observe better segmentations with T1 scans than with T1-weighted scans.

T-FAKE: Synthesizing Thermal Images for Facial Landmarking

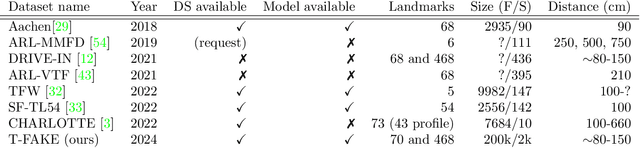
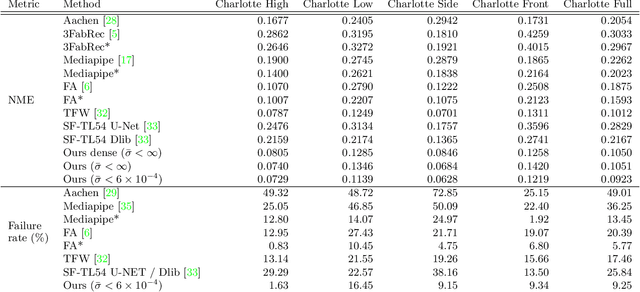
Facial analysis is a key component in a wide range of applications such as security, autonomous driving, entertainment, and healthcare. Despite the availability of various facial RGB datasets, the thermal modality, which plays a crucial role in life sciences, medicine, and biometrics, has been largely overlooked. To address this gap, we introduce the T-FAKE dataset, a new large-scale synthetic thermal dataset with sparse and dense landmarks. To facilitate the creation of the dataset, we propose a novel RGB2Thermal loss function, which enables the transfer of thermal style to RGB faces. By utilizing the Wasserstein distance between thermal and RGB patches and the statistical analysis of clinical temperature distributions on faces, we ensure that the generated thermal images closely resemble real samples. Using RGB2Thermal style transfer based on our RGB2Thermal loss function, we create the T-FAKE dataset, a large-scale synthetic thermal dataset of faces. Leveraging our novel T-FAKE dataset, probabilistic landmark prediction, and label adaptation networks, we demonstrate significant improvements in landmark detection methods on thermal images across different landmark conventions. Our models show excellent performance with both sparse 70-point landmarks and dense 478-point landmark annotations. Our code and models are available at https://github.com/phflot/tfake.

Learning from small data sets: Patch-based regularizers in inverse problems for image reconstruction

The solution of inverse problems is of fundamental interest in medical and astronomical imaging, geophysics as well as engineering and life sciences. Recent advances were made by using methods from machine learning, in particular deep neural networks. Most of these methods require a huge amount of (paired) data and computer capacity to train the networks, which often may not be available. Our paper addresses the issue of learning from small data sets by taking patches of very few images into account. We focus on the combination of model-based and data-driven methods by approximating just the image prior, also known as regularizer in the variational model. We review two methodically different approaches, namely optimizing the maximum log-likelihood of the patch distribution, and penalizing Wasserstein-like discrepancies of whole empirical patch distributions. From the point of view of Bayesian inverse problems, we show how we can achieve uncertainty quantification by approximating the posterior using Langevin Monte Carlo methods. We demonstrate the power of the methods in computed tomography, image super-resolution, and inpainting. Indeed, the approach provides also high-quality results in zero-shot super-resolution, where only a low-resolution image is available. The paper is accompanied by a GitHub repository containing implementations of all methods as well as data examples so that the reader can get their own insight into the performance.