Gabriele Steidl
Institute of Mathematics, Technische Universität Berlin
Adapting Noise to Data: Generative Flows from 1D Processes
Oct 14, 2025Abstract:We introduce a general framework for constructing generative models using one-dimensional noising processes. Beyond diffusion processes, we outline examples that demonstrate the flexibility of our approach. Motivated by this, we propose a novel framework in which the 1D processes themselves are learnable, achieved by parameterizing the noise distribution through quantile functions that adapt to the data. Our construction integrates seamlessly with standard objectives, including Flow Matching and consistency models. Learning quantile-based noise naturally captures heavy tails and compact supports when present. Numerical experiments highlight both the flexibility and the effectiveness of our method.
Provable Mixed-Noise Learning with Flow-Matching
Aug 25, 2025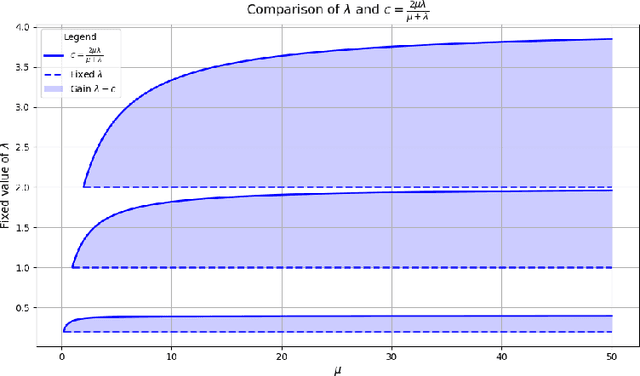

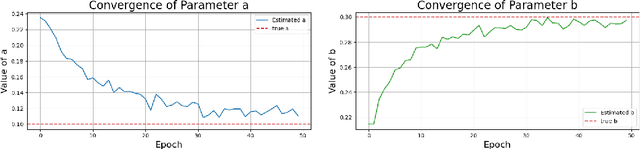
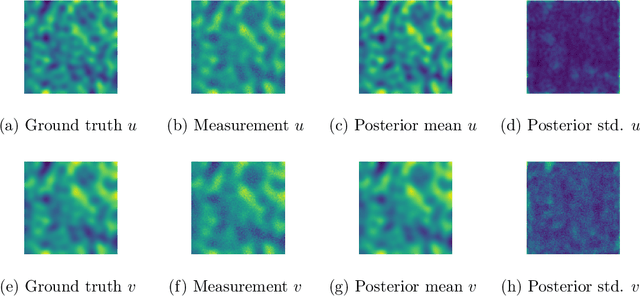
Abstract:We study Bayesian inverse problems with mixed noise, modeled as a combination of additive and multiplicative Gaussian components. While traditional inference methods often assume fixed or known noise characteristics, real-world applications, particularly in physics and chemistry, frequently involve noise with unknown and heterogeneous structure. Motivated by recent advances in flow-based generative modeling, we propose a novel inference framework based on conditional flow matching embedded within an Expectation-Maximization (EM) algorithm to jointly estimate posterior samplers and noise parameters. To enable high-dimensional inference and improve scalability, we use simulation-free ODE-based flow matching as the generative model in the E-step of the EM algorithm. We prove that, under suitable assumptions, the EM updates converge to the true noise parameters in the population limit of infinite observations. Our numerical results illustrate the effectiveness of combining EM inference with flow matching for mixed-noise Bayesian inverse problems.
Unsupervised Ground Metric Learning
Jul 17, 2025Abstract:Data classification without access to labeled samples remains a challenging problem. It usually depends on an appropriately chosen distance between features, a topic addressed in metric learning. Recently, Huizing, Cantini and Peyr\'e proposed to simultaneously learn optimal transport (OT) cost matrices between samples and features of the dataset. This leads to the task of finding positive eigenvectors of a certain nonlinear function that maps cost matrices to OT distances. Having this basic idea in mind, we consider both the algorithmic and the modeling part of unsupervised metric learning. First, we examine appropriate algorithms and their convergence. In particular, we propose to use the stochastic random function iteration algorithm and prove that it converges linearly for our setting, although our operators are not paracontractive as it was required for convergence so far. Second, we ask the natural question if the OT distance can be replaced by other distances. We show how Mahalanobis-like distances fit into our considerations. Further, we examine an approach via graph Laplacians. In contrast to the previous settings, we have just to deal with linear functions in the wanted matrices here, so that simple algorithms from linear algebra can be applied.
Smoothed Distance Kernels for MMDs and Applications in Wasserstein Gradient Flows
Apr 10, 2025Abstract:Negative distance kernels $K(x,y) := - \|x-y\|$ were used in the definition of maximum mean discrepancies (MMDs) in statistics and lead to favorable numerical results in various applications. In particular, so-called slicing techniques for handling high-dimensional kernel summations profit from the simple parameter-free structure of the distance kernel. However, due to its non-smoothness in $x=y$, most of the classical theoretical results, e.g. on Wasserstein gradient flows of the corresponding MMD functional do not longer hold true. In this paper, we propose a new kernel which keeps the favorable properties of the negative distance kernel as being conditionally positive definite of order one with a nearly linear increase towards infinity and a simple slicing structure, but is Lipschitz differentiable now. Our construction is based on a simple 1D smoothing procedure of the absolute value function followed by a Riemann-Liouville fractional integral transform. Numerical results demonstrate that the new kernel performs similarly well as the negative distance kernel in gradient descent methods, but now with theoretical guarantees.
Joint Metric Space Embedding by Unbalanced OT with Gromov-Wasserstein Marginal Penalization
Feb 11, 2025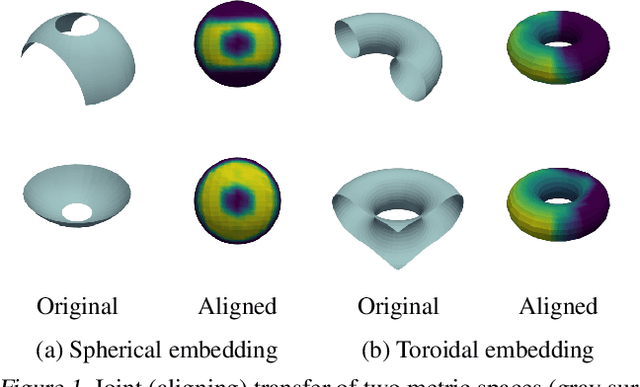
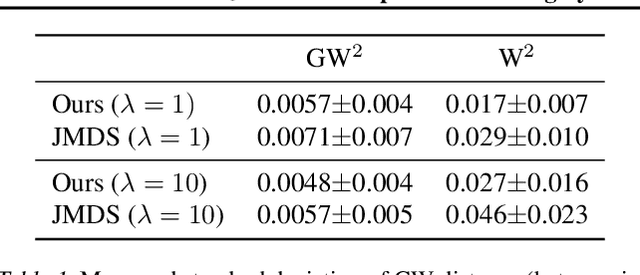
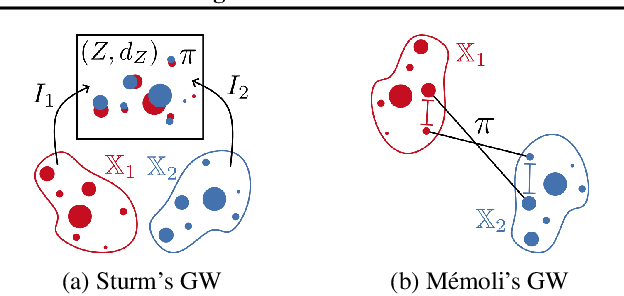
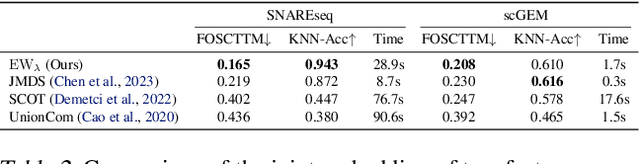
Abstract:We propose a new approach for unsupervised alignment of heterogeneous datasets, which maps data from two different domains without any known correspondences to a common metric space. Our method is based on an unbalanced optimal transport problem with Gromov-Wasserstein marginal penalization. It can be seen as a counterpart to the recently introduced joint multidimensional scaling method. We prove that there exists a minimizer of our functional and that for penalization parameters going to infinity, the corresponding sequence of minimizers converges to a minimizer of the so-called embedded Wasserstein distance. Our model can be reformulated as a quadratic, multi-marginal, unbalanced optimal transport problem, for which a bi-convex relaxation admits a numerical solver via block-coordinate descent. We provide numerical examples for joint embeddings in Euclidean as well as non-Euclidean spaces.
Flow Matching: Markov Kernels, Stochastic Processes and Transport Plans
Jan 28, 2025Abstract:Among generative neural models, flow matching techniques stand out for their simple applicability and good scaling properties. Here, velocity fields of curves connecting a simple latent and a target distribution are learned. Then the corresponding ordinary differential equation can be used to sample from a target distribution, starting in samples from the latent one. This paper reviews from a mathematical point of view different techniques to learn the velocity fields of absolutely continuous curves in the Wasserstein geometry. We show how the velocity fields can be characterized and learned via i) transport plans (couplings) between latent and target distributions, ii) Markov kernels and iii) stochastic processes, where the latter two include the coupling approach, but are in general broader. Besides this main goal, we show how flow matching can be used for solving Bayesian inverse problems, where the definition of conditional Wasserstein distances plays a central role. Finally, we briefly address continuous normalizing flows and score matching techniques, which approach the learning of velocity fields of curves from other directions.
Variable Bregman Majorization-Minimization Algorithm and its Application to Dirichlet Maximum Likelihood Estimation
Jan 13, 2025Abstract:We propose a novel Bregman descent algorithm for minimizing a convex function that is expressed as the sum of a differentiable part (defined over an open set) and a possibly nonsmooth term. The approach, referred to as the Variable Bregman Majorization-Minimization (VBMM) algorithm, extends the Bregman Proximal Gradient method by allowing the Bregman function used in the divergence to adaptively vary at each iteration, provided it satisfies a majorizing condition on the objective function. This adaptive framework enables the algorithm to approximate the objective more precisely at each iteration, thereby allowing for accelerated convergence compared to the traditional Bregman Proximal Gradient descent. We establish the convergence of the VBMM algorithm to a minimizer under mild assumptions on the family of metrics used. Furthermore, we introduce a novel application of both the Bregman Proximal Gradient method and the VBMM algorithm to the estimation of the multidimensional parameters of a Dirichlet distribution through the maximization of its log-likelihood. Numerical experiments confirm that the VBMM algorithm outperforms existing approaches in terms of convergence speed.
Sampling from Boltzmann densities with physics informed low-rank formats
Dec 10, 2024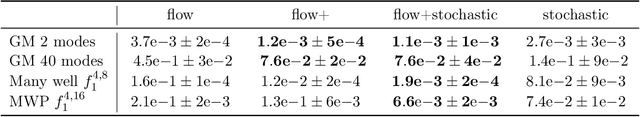
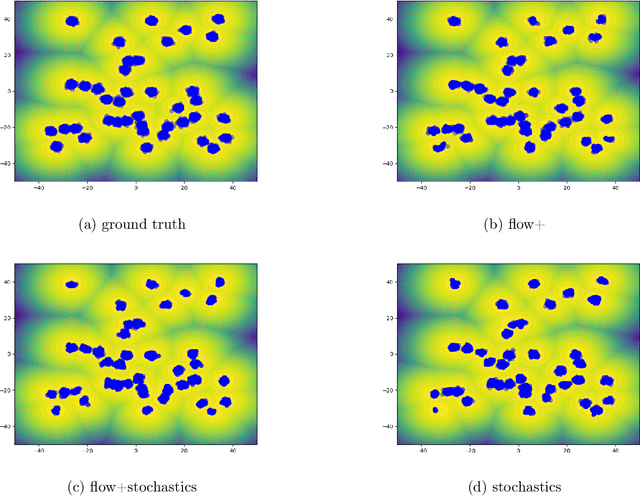
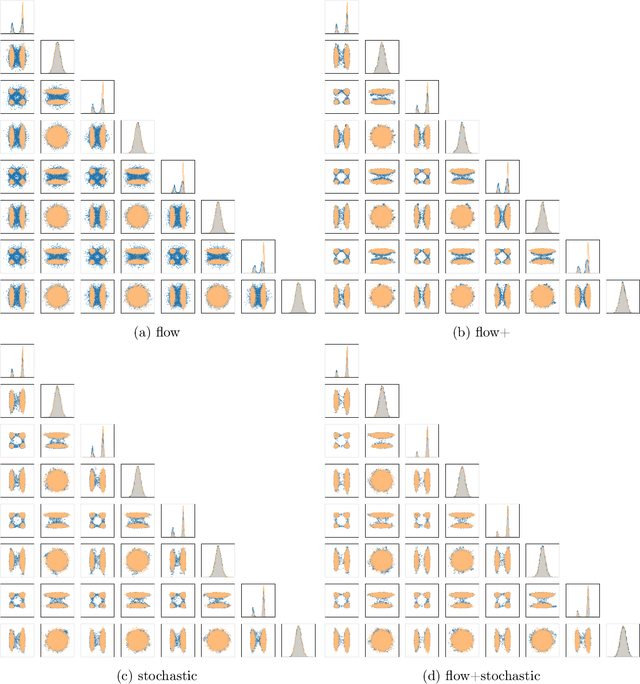
Abstract:Our method proposes the efficient generation of samples from an unnormalized Boltzmann density by solving the underlying continuity equation in the low-rank tensor train (TT) format. It is based on the annealing path commonly used in MCMC literature, which is given by the linear interpolation in the space of energies. Inspired by Sequential Monte Carlo, we alternate between deterministic time steps from the TT representation of the flow field and stochastic steps, which include Langevin and resampling steps. These adjust the relative weights of the different modes of the target distribution and anneal to the correct path distribution. We showcase the efficiency of our method on multiple numerical examples.
Optimizing Federated Learning by Entropy-Based Client Selection
Nov 02, 2024Abstract:Deep learning is an emerging field revolutionizing various industries, including natural language processing, computer vision, and many more. These domains typically require an extensive amount of data for optimal performance, potentially utilizing huge centralized data repositories. However, such centralization could raise privacy issues concerning the storage of sensitive data. To address this issue, federated learning was developed. It is a newly distributed learning technique that enables to collaboratively train a deep learning model on decentralized devices, referred to as clients, without compromising their data privacy. Traditional federated learning methods often suffer from severe performance degradation when the data distribution among clients differs significantly. This becomes especially problematic in the case of label distribution skew, where the distribution of labels varies across clients. To address this, a novel method called FedEntOpt is proposed. FedEntOpt is designed to mitigate performance issues caused by label distribution skew by maximizing the entropy of the global label distribution of the selected client subset in each federated learning round. This ensures that the aggregated model parameters from the clients were exhibited to data from all available labels, which improves the accuracy of the global model. Extensive experiments on several benchmark datasets show that the proposed method outperforms several state-of-the-art algorithms by up to 6% in classification accuracy, demonstrating robust and superior performance, particularly under low participation rates. In addition, it offers the flexibility to be combined with them, enhancing their performance by over 40%.
Conditional Generative Models for Contrast-Enhanced Synthesis of T1w and T1 Maps in Brain MRI
Oct 11, 2024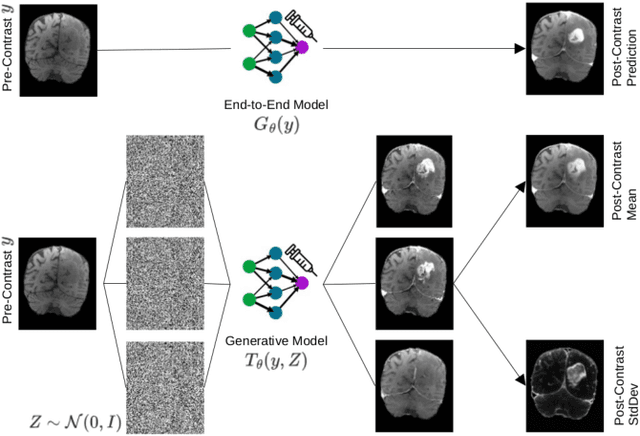

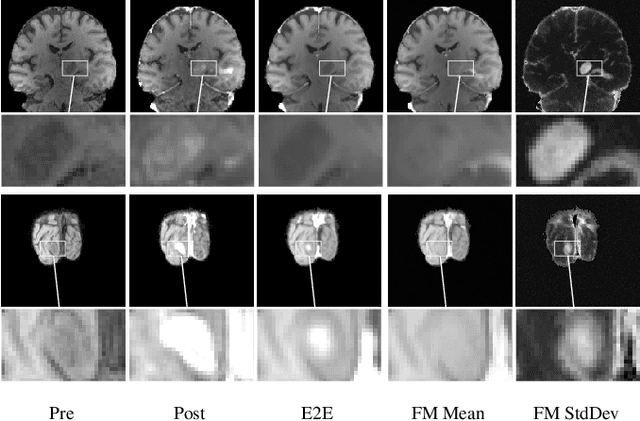
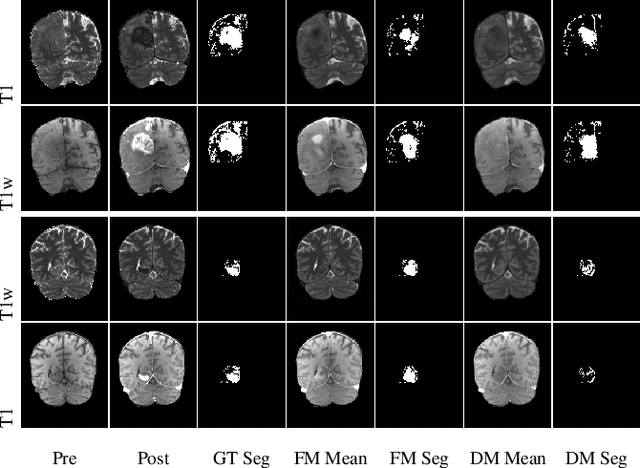
Abstract:Contrast enhancement by Gadolinium-based contrast agents (GBCAs) is a vital tool for tumor diagnosis in neuroradiology. Based on brain MRI scans of glioblastoma before and after Gadolinium administration, we address enhancement prediction by neural networks with two new contributions. Firstly, we study the potential of generative models, more precisely conditional diffusion and flow matching, for uncertainty quantification in virtual enhancement. Secondly, we examine the performance of T1 scans from quantitive MRI versus T1-weighted scans. In contrast to T1-weighted scans, these scans have the advantage of a physically meaningful and thereby comparable voxel range. To compare network prediction performance of these two modalities with incompatible gray-value scales, we propose to evaluate segmentations of contrast-enhanced regions of interest using Dice and Jaccard scores. Across models, we observe better segmentations with T1 scans than with T1-weighted scans.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge