Learning Brenier Potentials with Convex Generative Adversarial Neural Networks

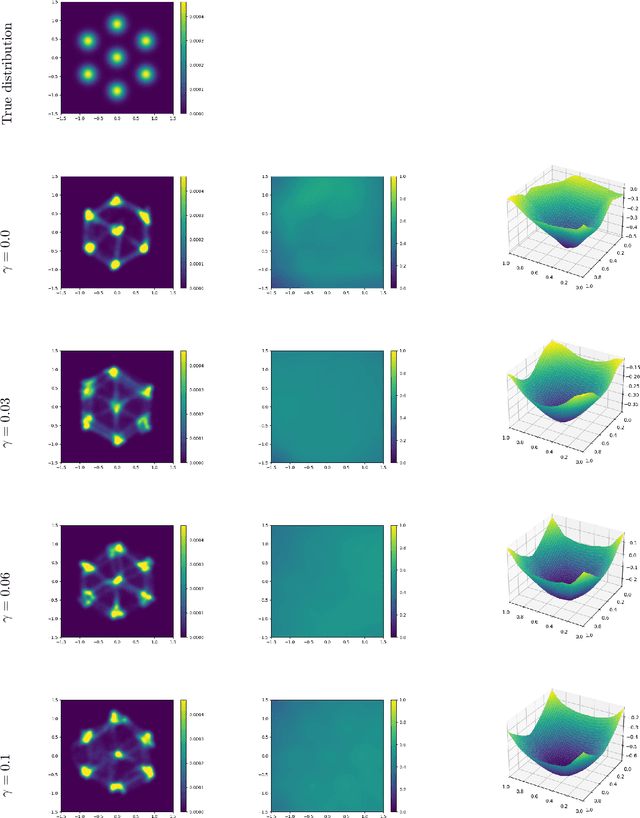
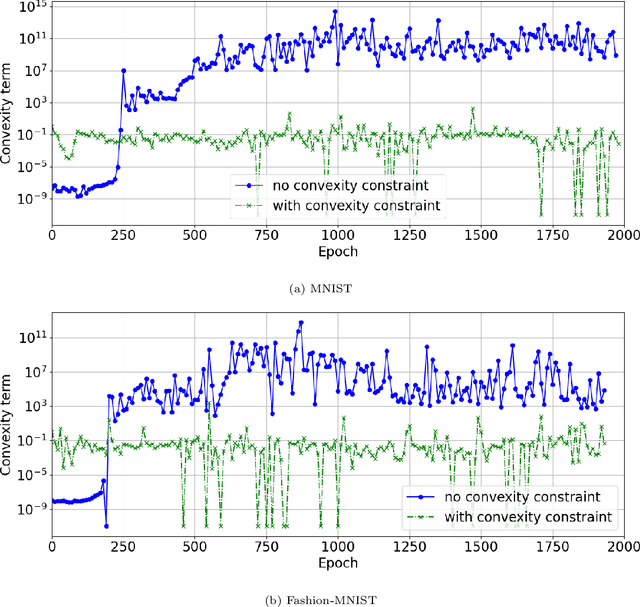
Brenier proved that under certain conditions on a source and a target probability measure there exists a strictly convex function such that its gradient is a transport map from the source to the target distribution. This function is called the Brenier potential. Furthermore, detailed information on the H\"older regularity of the Brenier potential is available. In this work we develop the statistical learning theory of generative adversarial neural networks that learn the Brenier potential. As by the transformation of densities formula, the density of the generated measure depends on the second derivative of the Brenier potential, we develop the universal approximation theory of ReCU networks with cubic activation $\mathtt{ReCU}(x)=\max\{0,x\}^3$ that combines the favorable approximation properties of H\"older functions with a Lipschitz continuous density. In order to assure the convexity of such general networks, we introduce an adversarial training procedure for a potential function represented by the ReCU networks that combines the classical discriminator cross entropy loss with a penalty term that enforces (strict) convexity. We give a detailed decomposition of learning errors and show that for a suitable high penalty parameter all networks chosen in the adversarial min-max optimization problem are strictly convex. This is further exploited to prove the consistency of the learning procedure for (slowly) expanding network capacity. We also implement the described learning algorithm and apply it to a number of standard test cases from Gaussian mixture to image data as target distributions. As predicted in theory, we observe that the convexity loss becomes inactive during the training process and the potentials represented by the neural networks have learned convexity.

Deep Generative Clustering with VAEs and Expectation-Maximization

We propose a novel deep clustering method that integrates Variational Autoencoders (VAEs) into the Expectation-Maximization (EM) framework. Our approach models the probability distribution of each cluster with a VAE and alternates between updating model parameters by maximizing the Evidence Lower Bound (ELBO) of the log-likelihood and refining cluster assignments based on the learned distributions. This enables effective clustering and generation of new samples from each cluster. Unlike existing VAE-based methods, our approach eliminates the need for a Gaussian Mixture Model (GMM) prior or additional regularization techniques. Experiments on MNIST and FashionMNIST demonstrate superior clustering performance compared to state-of-the-art methods.

Variable Bregman Majorization-Minimization Algorithm and its Application to Dirichlet Maximum Likelihood Estimation

We propose a novel Bregman descent algorithm for minimizing a convex function that is expressed as the sum of a differentiable part (defined over an open set) and a possibly nonsmooth term. The approach, referred to as the Variable Bregman Majorization-Minimization (VBMM) algorithm, extends the Bregman Proximal Gradient method by allowing the Bregman function used in the divergence to adaptively vary at each iteration, provided it satisfies a majorizing condition on the objective function. This adaptive framework enables the algorithm to approximate the objective more precisely at each iteration, thereby allowing for accelerated convergence compared to the traditional Bregman Proximal Gradient descent. We establish the convergence of the VBMM algorithm to a minimizer under mild assumptions on the family of metrics used. Furthermore, we introduce a novel application of both the Bregman Proximal Gradient method and the VBMM algorithm to the estimation of the multidimensional parameters of a Dirichlet distribution through the maximization of its log-likelihood. Numerical experiments confirm that the VBMM algorithm outperforms existing approaches in terms of convergence speed.

PnP-Flow: Plug-and-Play Image Restoration with Flow Matching

In this paper, we introduce Plug-and-Play (PnP) Flow Matching, an algorithm for solving imaging inverse problems. PnP methods leverage the strength of pre-trained denoisers, often deep neural networks, by integrating them in optimization schemes. While they achieve state-of-the-art performance on various inverse problems in imaging, PnP approaches face inherent limitations on more generative tasks like inpainting. On the other hand, generative models such as Flow Matching pushed the boundary in image sampling yet lack a clear method for efficient use in image restoration. We propose to combine the PnP framework with Flow Matching (FM) by defining a time-dependent denoiser using a pre-trained FM model. Our algorithm alternates between gradient descent steps on the data-fidelity term, reprojections onto the learned FM path, and denoising. Notably, our method is computationally efficient and memory-friendly, as it avoids backpropagation through ODEs and trace computations. We evaluate its performance on denoising, super-resolution, deblurring, and inpainting tasks, demonstrating superior results compared to existing PnP algorithms and Flow Matching based state-of-the-art methods.

A Novel Variational Approach for Multiphoton Microscopy Image Restoration: from PSF Estimation to 3D Deconvolution

In multi-photon microscopy (MPM), a recent in-vivo fluorescence microscopy system, the task of image restoration can be decomposed into two interlinked inverse problems: firstly, the characterization of the Point Spread Function (PSF) and subsequently, the deconvolution (i.e., deblurring) to remove the PSF effect, and reduce noise. The acquired MPM image quality is critically affected by PSF blurring and intense noise. The PSF in MPM is highly spread in 3D and is not well characterized, presenting high variability with respect to the observed objects. This makes the restoration of MPM images challenging. Common PSF estimation methods in fluorescence microscopy, including MPM, involve capturing images of sub-resolution beads, followed by quantifying the resulting ellipsoidal 3D spot. In this work, we revisit this approach, coping with its inherent limitations in terms of accuracy and practicality. We estimate the PSF from the observation of relatively large beads (approximately 1$\mu$m in diameter). This goes through the formulation and resolution of an original non-convex minimization problem, for which we propose a proximal alternating method along with convergence guarantees. Following the PSF estimation step, we then introduce an innovative strategy to deal with the high level multiplicative noise degrading the acquisitions. We rely on a heteroscedastic noise model for which we estimate the parameters. We then solve a constrained optimization problem to restore the image, accounting for the estimated PSF and noise, while allowing a minimal hyper-parameter tuning. Theoretical guarantees are given for the restoration algorithm. These algorithmic contributions lead to an end-to-end pipeline for 3D image restoration in MPM, that we share as a publicly available Python software. We demonstrate its effectiveness through several experiments on both simulated and real data.

A transductive few-shot learning approach for classification of digital histopathological slides from liver cancer

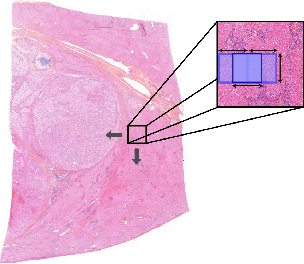
This paper presents a new approach for classifying 2D histopathology patches using few-shot learning. The method is designed to tackle a significant challenge in histopathology, which is the limited availability of labeled data. By applying a sliding window technique to histopathology slides, we illustrate the practical benefits of transductive learning (i.e., making joint predictions on patches) to achieve consistent and accurate classification. Our approach involves an optimization-based strategy that actively penalizes the prediction of a large number of distinct classes within each window. We conducted experiments on histopathological data to classify tissue classes in digital slides of liver cancer, specifically hepatocellular carcinoma. The initial results show the effectiveness of our method and its potential to enhance the process of automated cancer diagnosis and treatment, all while reducing the time and effort required for expert annotation.

Towards Practical Few-Shot Query Sets: Transductive Minimum Description Length Inference

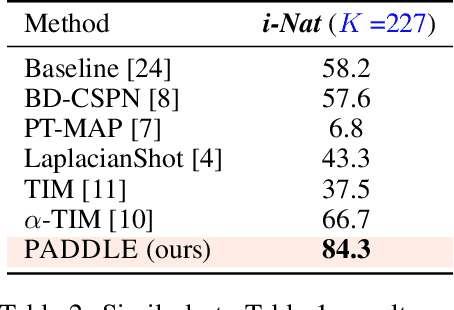
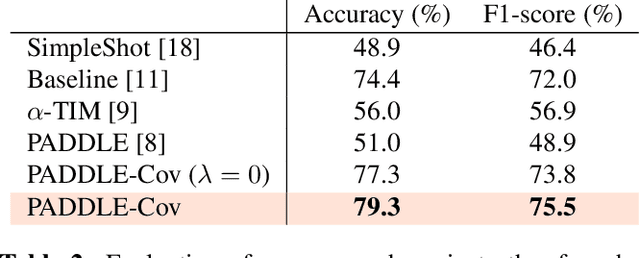
Standard few-shot benchmarks are often built upon simplifying assumptions on the query sets, which may not always hold in practice. In particular, for each task at testing time, the classes effectively present in the unlabeled query set are known a priori, and correspond exactly to the set of classes represented in the labeled support set. We relax these assumptions and extend current benchmarks, so that the query-set classes of a given task are unknown, but just belong to a much larger set of possible classes. Our setting could be viewed as an instance of the challenging yet practical problem of extremely imbalanced K-way classification, K being much larger than the values typically used in standard benchmarks, and with potentially irrelevant supervision from the support set. Expectedly, our setting incurs drops in the performances of state-of-the-art methods. Motivated by these observations, we introduce a PrimAl Dual Minimum Description LEngth (PADDLE) formulation, which balances data-fitting accuracy and model complexity for a given few-shot task, under supervision constraints from the support set. Our constrained MDL-like objective promotes competition among a large set of possible classes, preserving only effective classes that befit better the data of a few-shot task. It is hyperparameter free, and could be applied on top of any base-class training. Furthermore, we derive a fast block coordinate descent algorithm for optimizing our objective, with convergence guarantee, and a linear computational complexity at each iteration. Comprehensive experiments over the standard few-shot datasets and the more realistic and challenging i-Nat dataset show highly competitive performances of our method, more so when the numbers of possible classes in the tasks increase. Our code is publicly available at https://github.com/SegoleneMartin/PADDLE.