Provable Mixed-Noise Learning with Flow-Matching

We study Bayesian inverse problems with mixed noise, modeled as a combination of additive and multiplicative Gaussian components. While traditional inference methods often assume fixed or known noise characteristics, real-world applications, particularly in physics and chemistry, frequently involve noise with unknown and heterogeneous structure. Motivated by recent advances in flow-based generative modeling, we propose a novel inference framework based on conditional flow matching embedded within an Expectation-Maximization (EM) algorithm to jointly estimate posterior samplers and noise parameters. To enable high-dimensional inference and improve scalability, we use simulation-free ODE-based flow matching as the generative model in the E-step of the EM algorithm. We prove that, under suitable assumptions, the EM updates converge to the true noise parameters in the population limit of infinite observations. Our numerical results illustrate the effectiveness of combining EM inference with flow matching for mixed-noise Bayesian inverse problems.

Sampling from Boltzmann densities with physics informed low-rank formats

Our method proposes the efficient generation of samples from an unnormalized Boltzmann density by solving the underlying continuity equation in the low-rank tensor train (TT) format. It is based on the annealing path commonly used in MCMC literature, which is given by the linear interpolation in the space of energies. Inspired by Sequential Monte Carlo, we alternate between deterministic time steps from the TT representation of the flow field and stochastic steps, which include Langevin and resampling steps. These adjust the relative weights of the different modes of the target distribution and anneal to the correct path distribution. We showcase the efficiency of our method on multiple numerical examples.

PnP-Flow: Plug-and-Play Image Restoration with Flow Matching

In this paper, we introduce Plug-and-Play (PnP) Flow Matching, an algorithm for solving imaging inverse problems. PnP methods leverage the strength of pre-trained denoisers, often deep neural networks, by integrating them in optimization schemes. While they achieve state-of-the-art performance on various inverse problems in imaging, PnP approaches face inherent limitations on more generative tasks like inpainting. On the other hand, generative models such as Flow Matching pushed the boundary in image sampling yet lack a clear method for efficient use in image restoration. We propose to combine the PnP framework with Flow Matching (FM) by defining a time-dependent denoiser using a pre-trained FM model. Our algorithm alternates between gradient descent steps on the data-fidelity term, reprojections onto the learned FM path, and denoising. Notably, our method is computationally efficient and memory-friendly, as it avoids backpropagation through ODEs and trace computations. We evaluate its performance on denoising, super-resolution, deblurring, and inpainting tasks, demonstrating superior results compared to existing PnP algorithms and Flow Matching based state-of-the-art methods.

Conditional Wasserstein Distances with Applications in Bayesian OT Flow Matching

In inverse problems, many conditional generative models approximate the posterior measure by minimizing a distance between the joint measure and its learned approximation. While this approach also controls the distance between the posterior measures in the case of the Kullback--Leibler divergence, this is in general not hold true for the Wasserstein distance. In this paper, we introduce a conditional Wasserstein distance via a set of restricted couplings that equals the expected Wasserstein distance of the posteriors. Interestingly, the dual formulation of the conditional Wasserstein-1 flow resembles losses in the conditional Wasserstein GAN literature in a quite natural way. We derive theoretical properties of the conditional Wasserstein distance, characterize the corresponding geodesics and velocity fields as well as the flow ODEs. Subsequently, we propose to approximate the velocity fields by relaxing the conditional Wasserstein distance. Based on this, we propose an extension of OT Flow Matching for solving Bayesian inverse problems and demonstrate its numerical advantages on an inverse problem and class-conditional image generation.

Mixed Noise and Posterior Estimation with Conditional DeepGEM

Motivated by indirect measurements and applications from nanometrology with a mixed noise model, we develop a novel algorithm for jointly estimating the posterior and the noise parameters in Bayesian inverse problems. We propose to solve the problem by an expectation maximization (EM) algorithm. Based on the current noise parameters, we learn in the E-step a conditional normalizing flow that approximates the posterior. In the M-step, we propose to find the noise parameter updates again by an EM algorithm, which has analytical formulas. We compare the training of the conditional normalizing flow with the forward and reverse KL, and show that our model is able to incorporate information from many measurements, unlike previous approaches.

Learning from small data sets: Patch-based regularizers in inverse problems for image reconstruction

The solution of inverse problems is of fundamental interest in medical and astronomical imaging, geophysics as well as engineering and life sciences. Recent advances were made by using methods from machine learning, in particular deep neural networks. Most of these methods require a huge amount of (paired) data and computer capacity to train the networks, which often may not be available. Our paper addresses the issue of learning from small data sets by taking patches of very few images into account. We focus on the combination of model-based and data-driven methods by approximating just the image prior, also known as regularizer in the variational model. We review two methodically different approaches, namely optimizing the maximum log-likelihood of the patch distribution, and penalizing Wasserstein-like discrepancies of whole empirical patch distributions. From the point of view of Bayesian inverse problems, we show how we can achieve uncertainty quantification by approximating the posterior using Langevin Monte Carlo methods. We demonstrate the power of the methods in computed tomography, image super-resolution, and inpainting. Indeed, the approach provides also high-quality results in zero-shot super-resolution, where only a low-resolution image is available. The paper is accompanied by a GitHub repository containing implementations of all methods as well as data examples so that the reader can get their own insight into the performance.

Y-Diagonal Couplings: Approximating Posteriors with Conditional Wasserstein Distances

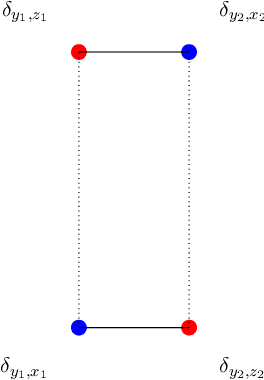
In inverse problems, many conditional generative models approximate the posterior measure by minimizing a distance between the joint measure and its learned approximation. While this approach also controls the distance between the posterior measures in the case of the Kullback Leibler divergence, it does not hold true for the Wasserstein distance. We will introduce a conditional Wasserstein distance with a set of restricted couplings that equals the expected Wasserstein distance of the posteriors. By deriving its dual, we find a rigorous way to motivate the loss of conditional Wasserstein GANs. We outline conditions under which the vanilla and the conditional Wasserstein distance coincide. Furthermore, we will show numerical examples where training with the conditional Wasserstein distance yields favorable properties for posterior sampling.

Posterior Sampling Based on Gradient Flows of the MMD with Negative Distance Kernel

We propose conditional flows of the maximum mean discrepancy (MMD) with the negative distance kernel for posterior sampling and conditional generative modeling. This MMD, which is also known as energy distance, has several advantageous properties like efficient computation via slicing and sorting. We approximate the joint distribution of the ground truth and the observations using discrete Wasserstein gradient flows and establish an error bound for the posterior distributions. Further, we prove that our particle flow is indeed a Wasserstein gradient flow of an appropriate functional. The power of our method is demonstrated by numerical examples including conditional image generation and inverse problems like superresolution, inpainting and computed tomography in low-dose and limited-angle settings.

Generative Sliced MMD Flows with Riesz Kernels

Maximum mean discrepancy (MMD) flows suffer from high computational costs in large scale computations. In this paper, we show that MMD flows with Riesz kernels $K(x,y) = - \|x-y\|^r$, $r \in (0,2)$ have exceptional properties which allow for their efficient computation. First, the MMD of Riesz kernels coincides with the MMD of their sliced version. As a consequence, the computation of gradients of MMDs can be performed in the one-dimensional setting. Here, for $r=1$, a simple sorting algorithm can be applied to reduce the complexity from $O(MN+N^2)$ to $O((M+N)\log(M+N))$ for two empirical measures with $M$ and $N$ support points. For the implementations we approximate the gradient of the sliced MMD by using only a finite number $P$ of slices. We show that the resulting error has complexity $O(\sqrt{d/P})$, where $d$ is the data dimension. These results enable us to train generative models by approximating MMD gradient flows by neural networks even for large scale applications. We demonstrate the efficiency of our model by image generation on MNIST, FashionMNIST and CIFAR10.

Conditional Generative Models are Provably Robust: Pointwise Guarantees for Bayesian Inverse Problems

Conditional generative models became a very powerful tool to sample from Bayesian inverse problem posteriors. It is well-known in classical Bayesian literature that posterior measures are quite robust with respect to perturbations of both the prior measure and the negative log-likelihood, which includes perturbations of the observations. However, to the best of our knowledge, the robustness of conditional generative models with respect to perturbations of the observations has not been investigated yet. In this paper, we prove for the first time that appropriately learned conditional generative models provide robust results for single observations.