Sampling from Boltzmann densities with physics informed low-rank formats

Our method proposes the efficient generation of samples from an unnormalized Boltzmann density by solving the underlying continuity equation in the low-rank tensor train (TT) format. It is based on the annealing path commonly used in MCMC literature, which is given by the linear interpolation in the space of energies. Inspired by Sequential Monte Carlo, we alternate between deterministic time steps from the TT representation of the flow field and stochastic steps, which include Langevin and resampling steps. These adjust the relative weights of the different modes of the target distribution and anneal to the correct path distribution. We showcase the efficiency of our method on multiple numerical examples.

Approximating Langevin Monte Carlo with ResNet-like Neural Network architectures

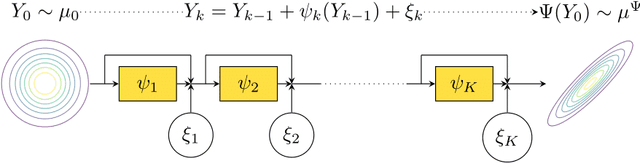
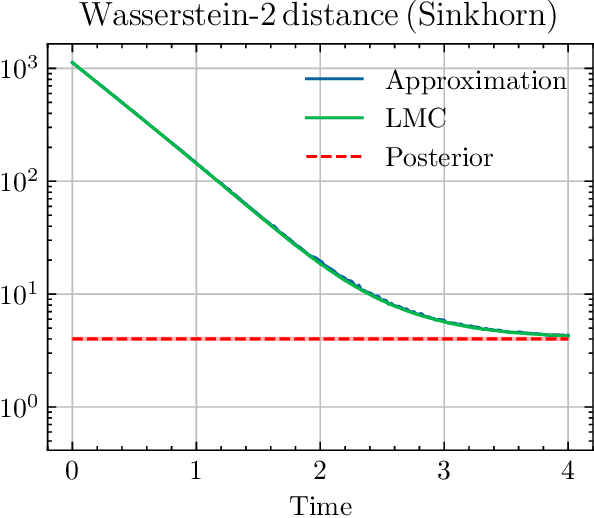
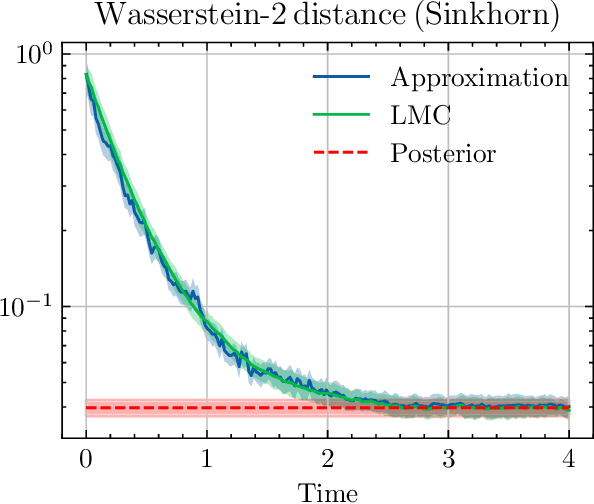
We sample from a given target distribution by constructing a neural network which maps samples from a simple reference, e.g. the standard normal distribution, to samples from the target. To that end, we propose using a neural network architecture inspired by the Langevin Monte Carlo (LMC) algorithm. Based on LMC perturbation results, we show approximation rates of the proposed architecture for smooth, log-concave target distributions measured in the Wasserstein-$2$ distance. The analysis heavily relies on the notion of sub-Gaussianity of the intermediate measures of the perturbed LMC process. In particular, we derive bounds on the growth of the intermediate variance proxies under different assumptions on the perturbations. Moreover, we propose an architecture similar to deep residual neural networks and derive expressivity results for approximating the sample to target distribution map.