Approximation and learning with compositional tensor trains

We introduce compositional tensor trains (CTTs) for the approximation of multivariate functions, a class of models obtained by composing low-rank functions in the tensor-train format. This format can encode standard approximation tools, such as (sparse) polynomials, deep neural networks (DNNs) with fixed width, or tensor networks with arbitrary permutation of the inputs, or more general affine coordinate transformations, with similar complexities. This format can be viewed as a DNN with width exponential in the input dimension and structured weights matrices. Compared to DNNs, this format enables controlled compression at the layer level using efficient tensor algebra. On the optimization side, we derive a layerwise algorithm inspired by natural gradient descent, allowing to exploit efficient low-rank tensor algebra. This relies on low-rank estimations of Gram matrices, and tensor structured random sketching. Viewing the format as a discrete dynamical system, we also derive an optimization algorithm inspired by numerical methods in optimal control. Numerical experiments on regression tasks demonstrate the expressivity of the new format and the relevance of the proposed optimization algorithms. Overall, CTTs combine the expressivity of compositional models with the algorithmic efficiency of tensor algebra, offering a scalable alternative to standard deep neural networks.

Sampling from Boltzmann densities with physics informed low-rank formats

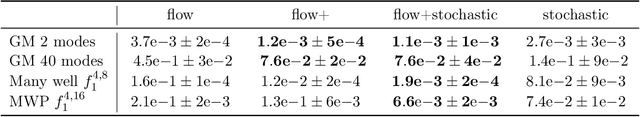
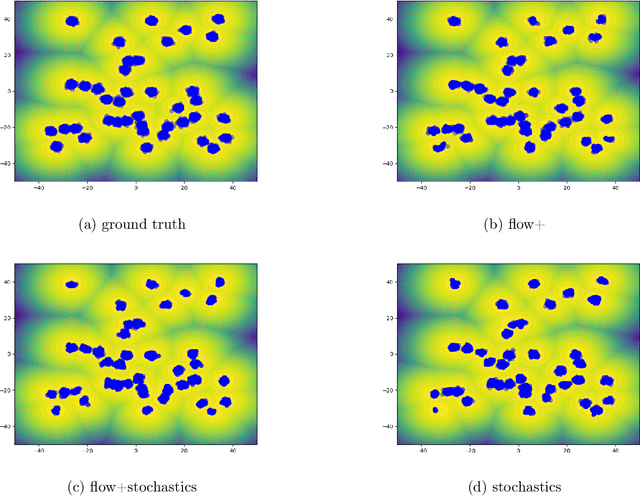
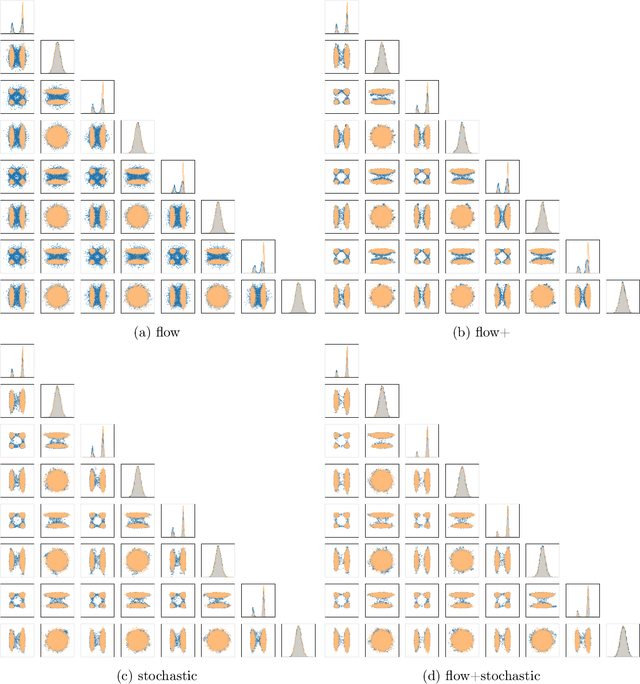
Our method proposes the efficient generation of samples from an unnormalized Boltzmann density by solving the underlying continuity equation in the low-rank tensor train (TT) format. It is based on the annealing path commonly used in MCMC literature, which is given by the linear interpolation in the space of energies. Inspired by Sequential Monte Carlo, we alternate between deterministic time steps from the TT representation of the flow field and stochastic steps, which include Langevin and resampling steps. These adjust the relative weights of the different modes of the target distribution and anneal to the correct path distribution. We showcase the efficiency of our method on multiple numerical examples.

Generative Modelling with Tensor Train approximations of Hamilton--Jacobi--Bellman equations

Sampling from probability densities is a common challenge in fields such as Uncertainty Quantification (UQ) and Generative Modelling (GM). In GM in particular, the use of reverse-time diffusion processes depending on the log-densities of Ornstein-Uhlenbeck forward processes are a popular sampling tool. In Berner et al. [2022] the authors point out that these log-densities can be obtained by solution of a \textit{Hamilton-Jacobi-Bellman} (HJB) equation known from stochastic optimal control. While this HJB equation is usually treated with indirect methods such as policy iteration and unsupervised training of black-box architectures like Neural Networks, we propose instead to solve the HJB equation by direct time integration, using compressed polynomials represented in the Tensor Train (TT) format for spatial discretization. Crucially, this method is sample-free, agnostic to normalization constants and can avoid the curse of dimensionality due to the TT compression. We provide a complete derivation of the HJB equation's action on Tensor Train polynomials and demonstrate the performance of the proposed time-step-, rank- and degree-adaptive integration method on a nonlinear sampling task in 20 dimensions.

Approximating Langevin Monte Carlo with ResNet-like Neural Network architectures

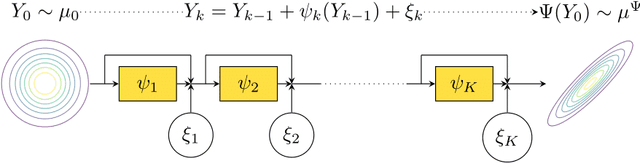
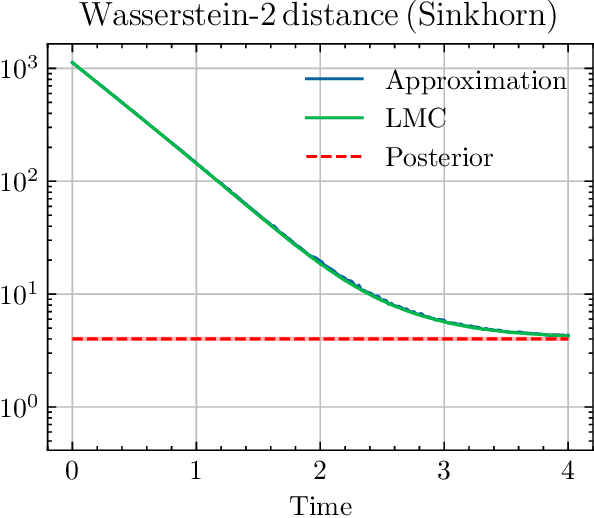
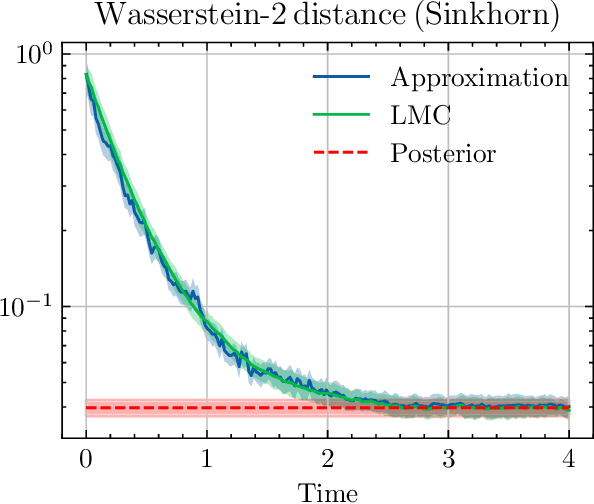
We sample from a given target distribution by constructing a neural network which maps samples from a simple reference, e.g. the standard normal distribution, to samples from the target. To that end, we propose using a neural network architecture inspired by the Langevin Monte Carlo (LMC) algorithm. Based on LMC perturbation results, we show approximation rates of the proposed architecture for smooth, log-concave target distributions measured in the Wasserstein-$2$ distance. The analysis heavily relies on the notion of sub-Gaussianity of the intermediate measures of the perturbed LMC process. In particular, we derive bounds on the growth of the intermediate variance proxies under different assumptions on the perturbations. Moreover, we propose an architecture similar to deep residual neural networks and derive expressivity results for approximating the sample to target distribution map.