Flow Matching: Markov Kernels, Stochastic Processes and Transport Plans

Among generative neural models, flow matching techniques stand out for their simple applicability and good scaling properties. Here, velocity fields of curves connecting a simple latent and a target distribution are learned. Then the corresponding ordinary differential equation can be used to sample from a target distribution, starting in samples from the latent one. This paper reviews from a mathematical point of view different techniques to learn the velocity fields of absolutely continuous curves in the Wasserstein geometry. We show how the velocity fields can be characterized and learned via i) transport plans (couplings) between latent and target distributions, ii) Markov kernels and iii) stochastic processes, where the latter two include the coupling approach, but are in general broader. Besides this main goal, we show how flow matching can be used for solving Bayesian inverse problems, where the definition of conditional Wasserstein distances plays a central role. Finally, we briefly address continuous normalizing flows and score matching techniques, which approach the learning of velocity fields of curves from other directions.

Neural Sampling from Boltzmann Densities: Fisher-Rao Curves in the Wasserstein Geometry

We deal with the task of sampling from an unnormalized Boltzmann density $\rho_D$ by learning a Boltzmann curve given by energies $f_t$ starting in a simple density $\rho_Z$. First, we examine conditions under which Fisher-Rao flows are absolutely continuous in the Wasserstein geometry. Second, we address specific interpolations $f_t$ and the learning of the related density/velocity pairs $(\rho_t,v_t)$. It was numerically observed that the linear interpolation, which requires only a parametrization of the velocity field $v_t$, suffers from a "teleportation-of-mass" issue. Using tools from the Wasserstein geometry, we give an analytical example, where we can precisely measure the explosion of the velocity field. Inspired by M\'at\'e and Fleuret, who parametrize both $f_t$ and $v_t$, we propose an interpolation which parametrizes only $f_t$ and fixes an appropriate $v_t$. This corresponds to the Wasserstein gradient flow of the Kullback-Leibler divergence related to Langevin dynamics. We demonstrate by numerical examples that our model provides a well-behaved flow field which successfully solves the above sampling task.

Conditional Wasserstein Distances with Applications in Bayesian OT Flow Matching

In inverse problems, many conditional generative models approximate the posterior measure by minimizing a distance between the joint measure and its learned approximation. While this approach also controls the distance between the posterior measures in the case of the Kullback--Leibler divergence, this is in general not hold true for the Wasserstein distance. In this paper, we introduce a conditional Wasserstein distance via a set of restricted couplings that equals the expected Wasserstein distance of the posteriors. Interestingly, the dual formulation of the conditional Wasserstein-1 flow resembles losses in the conditional Wasserstein GAN literature in a quite natural way. We derive theoretical properties of the conditional Wasserstein distance, characterize the corresponding geodesics and velocity fields as well as the flow ODEs. Subsequently, we propose to approximate the velocity fields by relaxing the conditional Wasserstein distance. Based on this, we propose an extension of OT Flow Matching for solving Bayesian inverse problems and demonstrate its numerical advantages on an inverse problem and class-conditional image generation.

Y-Diagonal Couplings: Approximating Posteriors with Conditional Wasserstein Distances

In inverse problems, many conditional generative models approximate the posterior measure by minimizing a distance between the joint measure and its learned approximation. While this approach also controls the distance between the posterior measures in the case of the Kullback Leibler divergence, it does not hold true for the Wasserstein distance. We will introduce a conditional Wasserstein distance with a set of restricted couplings that equals the expected Wasserstein distance of the posteriors. By deriving its dual, we find a rigorous way to motivate the loss of conditional Wasserstein GANs. We outline conditions under which the vanilla and the conditional Wasserstein distance coincide. Furthermore, we will show numerical examples where training with the conditional Wasserstein distance yields favorable properties for posterior sampling.

Generative Sliced MMD Flows with Riesz Kernels

Maximum mean discrepancy (MMD) flows suffer from high computational costs in large scale computations. In this paper, we show that MMD flows with Riesz kernels $K(x,y) = - \|x-y\|^r$, $r \in (0,2)$ have exceptional properties which allow for their efficient computation. First, the MMD of Riesz kernels coincides with the MMD of their sliced version. As a consequence, the computation of gradients of MMDs can be performed in the one-dimensional setting. Here, for $r=1$, a simple sorting algorithm can be applied to reduce the complexity from $O(MN+N^2)$ to $O((M+N)\log(M+N))$ for two empirical measures with $M$ and $N$ support points. For the implementations we approximate the gradient of the sliced MMD by using only a finite number $P$ of slices. We show that the resulting error has complexity $O(\sqrt{d/P})$, where $d$ is the data dimension. These results enable us to train generative models by approximating MMD gradient flows by neural networks even for large scale applications. We demonstrate the efficiency of our model by image generation on MNIST, FashionMNIST and CIFAR10.

Convolutional Dictionary Learning by End-To-End Training of Iterative Neural Networks

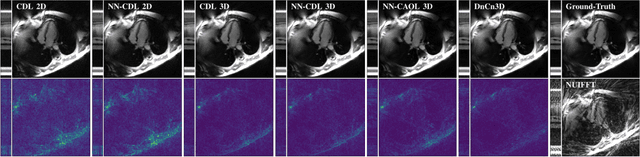
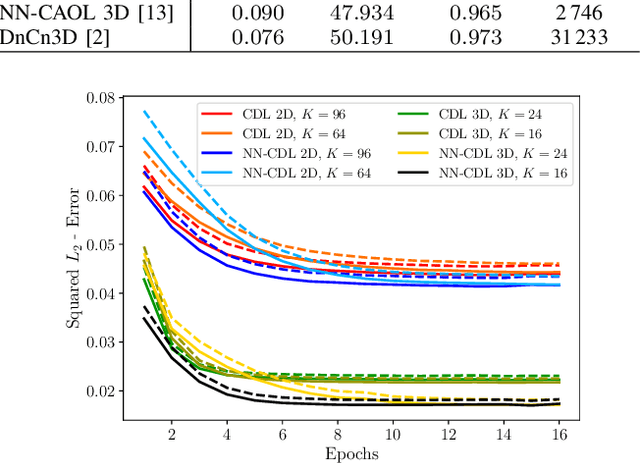
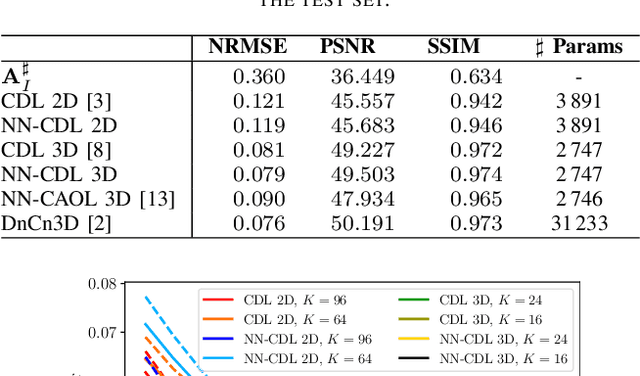
Sparsity-based methods have a long history in the field of signal processing and have been successfully applied to various image reconstruction problems. The involved sparsifying transformations or dictionaries are typically either pre-trained using a model which reflects the assumed properties of the signals or adaptively learned during the reconstruction - yielding so-called blind Compressed Sensing approaches. However, by doing so, the transforms are never explicitly trained in conjunction with the physical model which generates the signals. In addition, properly choosing the involved regularization parameters remains a challenging task. Another recently emerged training-paradigm for regularization methods is to use iterative neural networks (INNs) - also known as unrolled networks - which contain the physical model. In this work, we construct an INN which can be used as a supervised and physics-informed online convolutional dictionary learning algorithm. We evaluated the proposed approach by applying it to a realistic large-scale dynamic MR reconstruction problem and compared it to several other recently published works. We show that the proposed INN improves over two conventional model-agnostic training methods and yields competitive results also compared to a deep INN. Further, it does not require to choose the regularization parameters and - in contrast to deep INNs - each network component is entirely interpretable.

Convolutional Analysis Operator Learning by End-To-End Training of Iterative Neural Networks

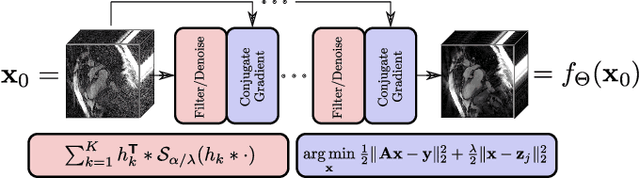
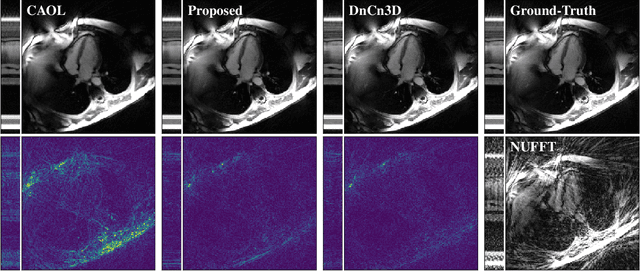
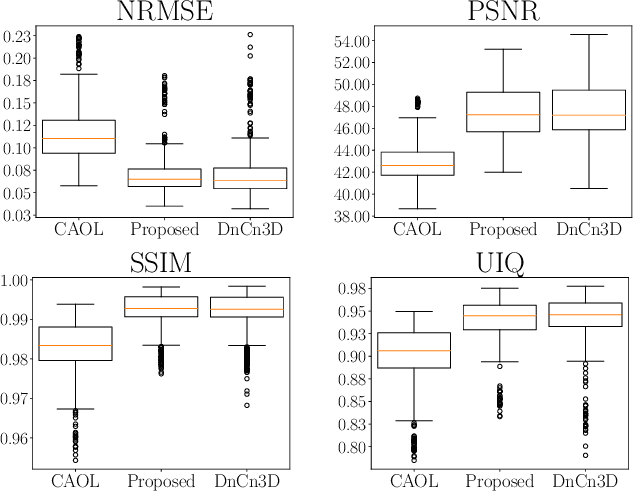
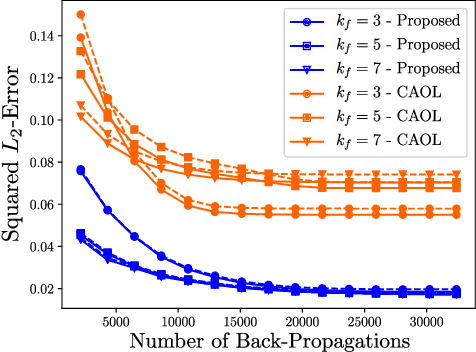
The concept of sparsity has been extensively applied for regularization in image reconstruction. Typically, sparsifying transforms are either pre-trained on ground-truth images or adaptively trained during the reconstruction. Thereby, learning algorithms are designed to minimize some target function which encodes the desired properties of the transform. However, this procedure ignores the subsequently employed reconstruction algorithm as well as the physical model which is responsible for the image formation process. Iterative neural networks - which contain the physical model - can overcome these issues. In this work, we demonstrate how convolutional sparsifying filters can be efficiently learned by end-to-end training of iterative neural networks. We evaluated our approach on a non-Cartesian 2D cardiac cine MRI example and show that the obtained filters are better suitable for the corresponding reconstruction algorithm than the ones obtained by decoupled pre-training.

Neural Networks-based Regularization for Large-Scale Medical Image Reconstruction

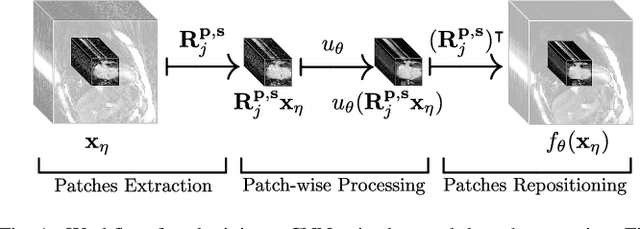
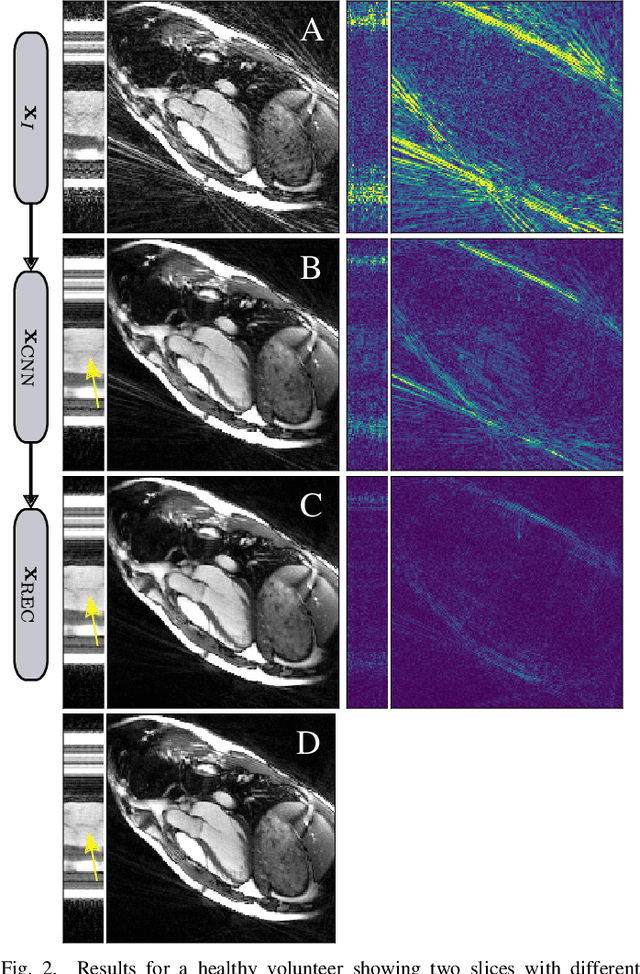
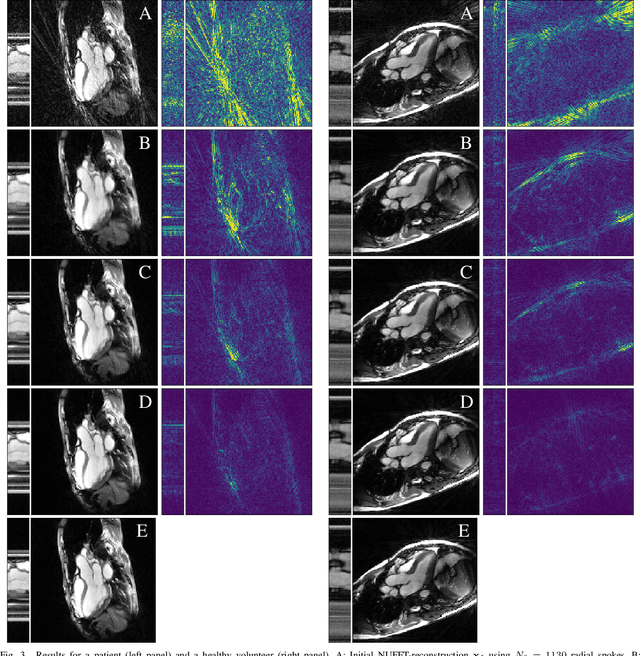
In this paper we present a generalized Deep Learning-based approach for solving ill-posed large-scale inverse problems occuring in medical image reconstruction. Recently, Deep Learning methods using iterative neural networks and cascaded neural networks have been reported to achieve state-of-the-art results with respect to various quantitative quality measures as PSNR, NRMSE and SSIM across different imaging modalities. However, the fact that these approaches employ the forward and adjoint operators repeatedly in the network architecture requires the network to process the whole images or volumes at once, which for some applications is computationally infeasible. In this work, we follow a different reconstruction strategy by decoupling the regularization of the solution from ensuring consistency with the measured data. The regularization is given in the form of an image prior obtained by the output of a previously trained neural network which is used in a Tikhonov regularization framework. By doing so, more complex and sophisticated network architectures can be used for the removal of the artefacts or noise than it is usually the case in iterative networks. Due to the large scale of the considered problems and the resulting computational complexity of the employed networks, the priors are obtained by processing the images or volumes as patches or slices. We evaluated the method for the cases of 3D cone-beam low dose CT and undersampled 2D radial cine MRI and compared it to a total variation-minimization-based reconstruction algorithm as well as to a method with regularization based on learned overcomplete dictionaries. The proposed method outperformed all the reported methods with respect to all chosen quantitative measures and further accelerates the regularization step in the reconstruction by several orders of magnitude.

Spatio-Temporal Deep Learning-Based Undersampling Artefact Reduction for 2D Radial Cine MRI with Limited Data

In this work we reduce undersampling artefacts in two-dimensional ($2D$) golden-angle radial cine cardiac MRI by applying a modified version of the U-net. We train the network on $2D$ spatio-temporal slices which are previously extracted from the image sequences. We compare our approach to two $2D$ and a $3D$ Deep Learning-based post processing methods and to three iterative reconstruction methods for dynamic cardiac MRI. Our method outperforms the $2D$ spatially trained U-net and the $2D$ spatio-temporal U-net. Compared to the $3D$ spatio-temporal U-net, our method delivers comparable results, but with shorter training times and less training data. Compared to the Compressed Sensing-based methods $kt$-FOCUSS and a total variation regularised reconstruction approach, our method improves image quality with respect to all reported metrics. Further, it achieves competitive results when compared to an iterative reconstruction method based on adaptive regularization with Dictionary Learning and total variation, while only requiring a small fraction of the computational time. A persistent homology analysis demonstrates that the data manifold of the spatio-temporal domain has a lower complexity than the spatial domain and therefore, the learning of a projection-like mapping is facilitated. Even when trained on only one single subject without data-augmentation, our approach yields results which are similar to the ones obtained on a large training dataset. This makes the method particularly suitable for training a network on limited training data. Finally, in contrast to the spatial $2D$ U-net, our proposed method is shown to be naturally robust with respect to image rotation in image space and almost achieves rotation-equivariance where neither data-augmentation nor a particular network design are required.