Fully automated quantification of in vivo viscoelasticity of prostate zones using magnetic resonance elastography with Dense U-net segmentation

Magnetic resonance elastography (MRE) for measuring viscoelasticity heavily depends on proper tissue segmentation, especially in heterogeneous organs such as the prostate. Using trained network-based image segmentation, we investigated if MRE data suffice to extract anatomical and viscoelastic information for automatic tabulation of zonal mechanical properties of the prostate. Overall, 40 patients with benign prostatic hyperplasia (BPH) or prostate cancer (PCa) were examined with three magnetic resonance imaging (MRI) sequences: T2-weighted MRI (T2w), diffusion-weighted imaging (DWI), and MRE-based tomoelastography yielding six independent sets of imaging data per patient (T2w, DWI, apparent diffusion coefficient (ADC), MRE magnitude, shear wave speed, and loss angle maps). Combinations of these data were used to train Dense U-nets with manually segmented masks of the entire prostate gland (PG), central zone (CZ), and peripheral zone (PZ) in 30 patients and to validate them in 10 patients. Dice score (DS), sensitivity, specificity, and Hausdorff distance were determined. We found that segmentation based on MRE magnitude maps alone (DS, PG: 0.93$\pm$0.04, CZ: 0.95$\pm$0.03, PZ: 0.77$\pm$0.05) was more accurate than magnitude maps combined with T2w and DWI_b (DS, PG: 0.91$\pm$0.04, CZ: 0.91$\pm$0.06, PZ: 0.63$\pm$0.16) or T2w alone (DS, PG: 0.92$\pm$0.03, CZ: 0.91$\pm$0.04, PZ: 0.65$\pm$0.08). Automatically tabulated MRE values were not different from ground-truth values (P>0.05). In conclusion: MRE combined with Dense U-net segmentation allows tabulation of quantitative imaging markers without manual analysis and independent of other MRI sequences and can thus contribute to PCa detection and classification.

Unsupervised Adaptive Neural Network Regularization for Accelerated Radial Cine MRI

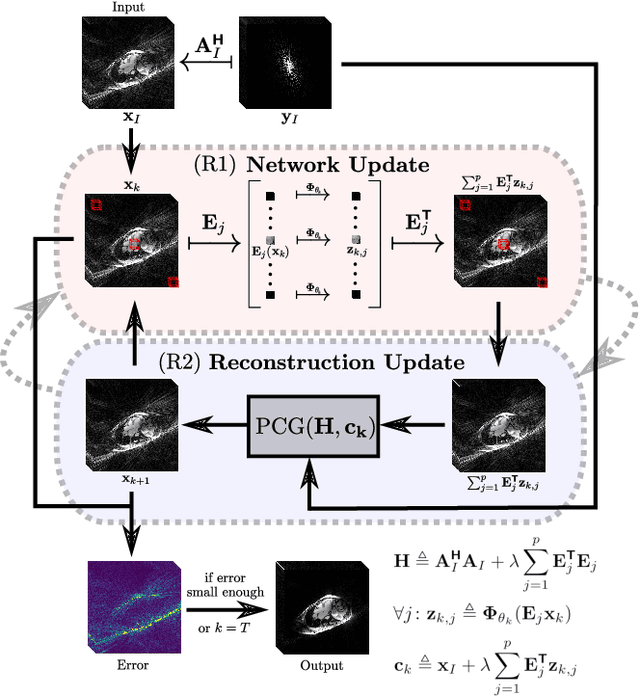
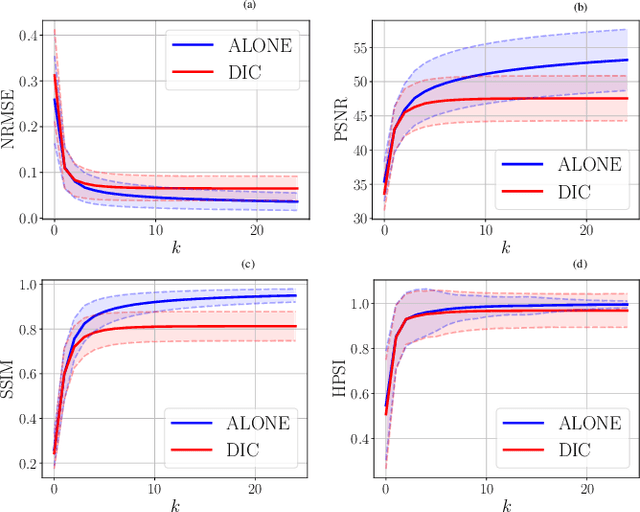
In this work, we propose an iterative reconstruction scheme (ALONE - Adaptive Learning Of NEtworks) for 2D radial cine MRI based on ground truth-free unsupervised learning of shallow convolutional neural networks. The network is trained to approximate patches of the current estimate of the solution during the reconstruction. By imposing a shallow network topology and constraining the $L_2$-norm of the learned filters, the network's representation power is limited in order not to be able to recover noise. Therefore, the network can be interpreted to perform a low dimensional approximation of the patches for stabilizing the inversion process. We compare the proposed reconstruction scheme to two ground truth-free reconstruction methods, namely a well known Total Variation (TV) minimization and an unsupervised adaptive Dictionary Learning (DIC) method. The proposed method outperforms both methods with respect to all reported quantitative measures. Further, in contrast to DIC, where the sparse approximation of the patches involves the solution of a complex optimization problem, ALONE only requires a forward pass of all patches through the shallow network and therefore significantly accelerates the reconstruction.

Neural Networks-based Regularization for Large-Scale Medical Image Reconstruction

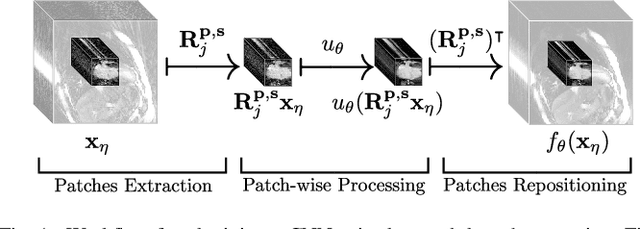
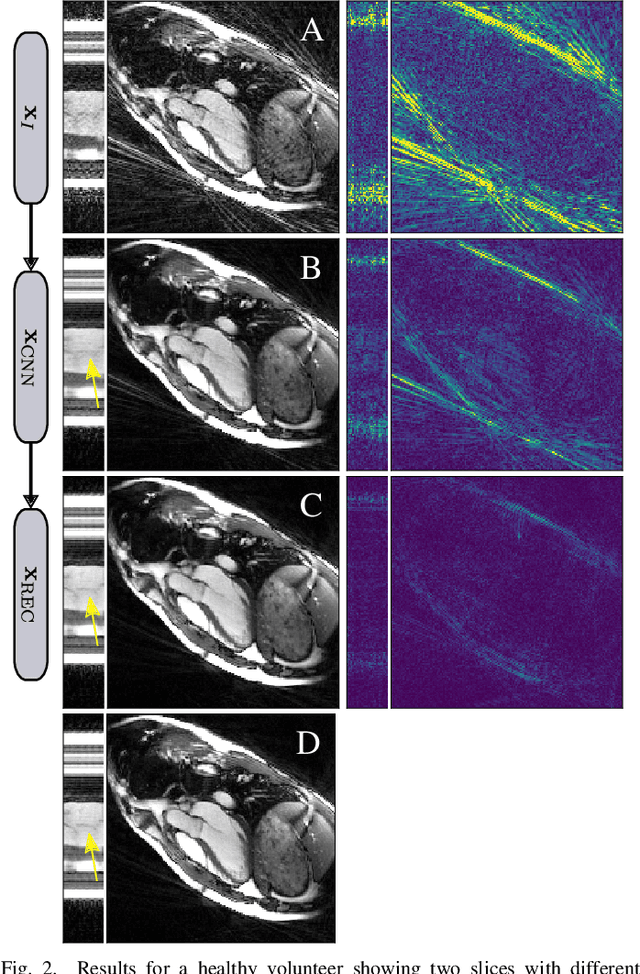
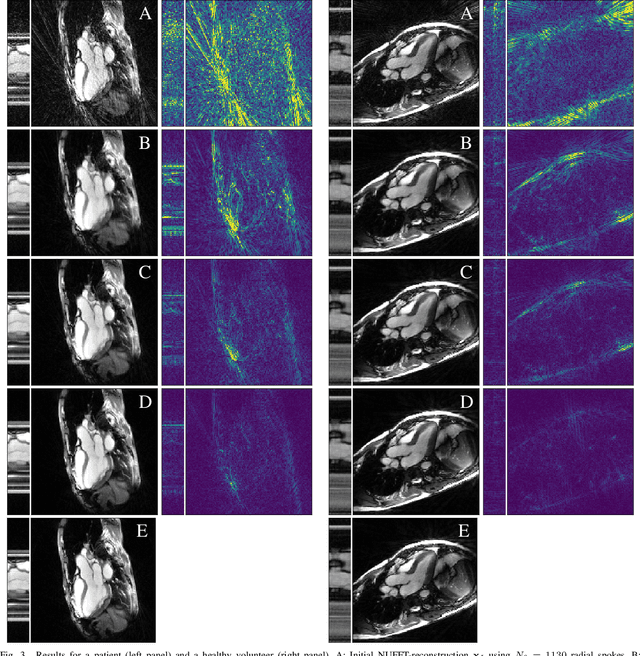
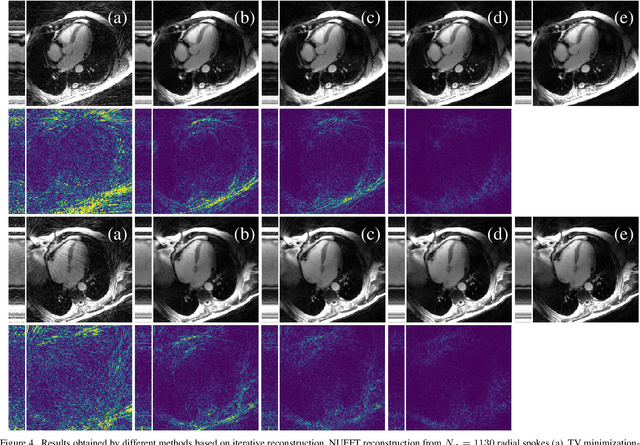
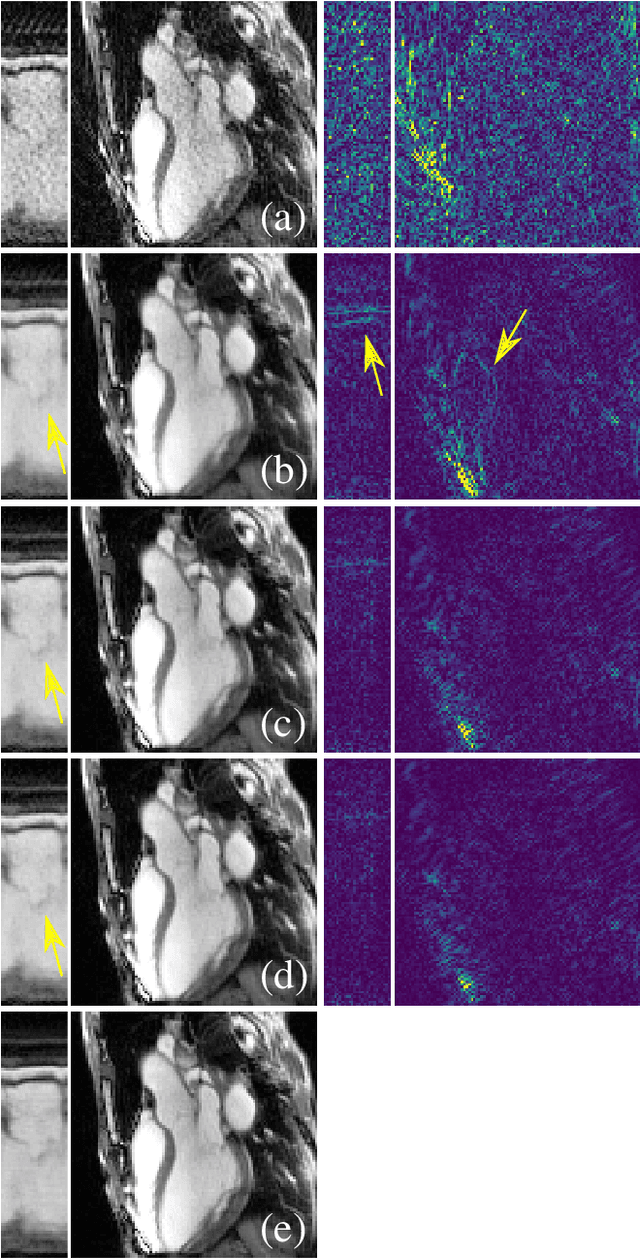
In this paper we present a generalized Deep Learning-based approach for solving ill-posed large-scale inverse problems occuring in medical image reconstruction. Recently, Deep Learning methods using iterative neural networks and cascaded neural networks have been reported to achieve state-of-the-art results with respect to various quantitative quality measures as PSNR, NRMSE and SSIM across different imaging modalities. However, the fact that these approaches employ the forward and adjoint operators repeatedly in the network architecture requires the network to process the whole images or volumes at once, which for some applications is computationally infeasible. In this work, we follow a different reconstruction strategy by decoupling the regularization of the solution from ensuring consistency with the measured data. The regularization is given in the form of an image prior obtained by the output of a previously trained neural network which is used in a Tikhonov regularization framework. By doing so, more complex and sophisticated network architectures can be used for the removal of the artefacts or noise than it is usually the case in iterative networks. Due to the large scale of the considered problems and the resulting computational complexity of the employed networks, the priors are obtained by processing the images or volumes as patches or slices. We evaluated the method for the cases of 3D cone-beam low dose CT and undersampled 2D radial cine MRI and compared it to a total variation-minimization-based reconstruction algorithm as well as to a method with regularization based on learned overcomplete dictionaries. The proposed method outperformed all the reported methods with respect to all chosen quantitative measures and further accelerates the regularization step in the reconstruction by several orders of magnitude.

Spatio-Temporal Deep Learning-Based Undersampling Artefact Reduction for 2D Radial Cine MRI with Limited Data

In this work we reduce undersampling artefacts in two-dimensional ($2D$) golden-angle radial cine cardiac MRI by applying a modified version of the U-net. We train the network on $2D$ spatio-temporal slices which are previously extracted from the image sequences. We compare our approach to two $2D$ and a $3D$ Deep Learning-based post processing methods and to three iterative reconstruction methods for dynamic cardiac MRI. Our method outperforms the $2D$ spatially trained U-net and the $2D$ spatio-temporal U-net. Compared to the $3D$ spatio-temporal U-net, our method delivers comparable results, but with shorter training times and less training data. Compared to the Compressed Sensing-based methods $kt$-FOCUSS and a total variation regularised reconstruction approach, our method improves image quality with respect to all reported metrics. Further, it achieves competitive results when compared to an iterative reconstruction method based on adaptive regularization with Dictionary Learning and total variation, while only requiring a small fraction of the computational time. A persistent homology analysis demonstrates that the data manifold of the spatio-temporal domain has a lower complexity than the spatial domain and therefore, the learning of a projection-like mapping is facilitated. Even when trained on only one single subject without data-augmentation, our approach yields results which are similar to the ones obtained on a large training dataset. This makes the method particularly suitable for training a network on limited training data. Finally, in contrast to the spatial $2D$ U-net, our proposed method is shown to be naturally robust with respect to image rotation in image space and almost achieves rotation-equivariance where neither data-augmentation nor a particular network design are required.