Learning Spatially Adaptive $\ell_1$-Norms Weights for Convolutional Synthesis Regularization

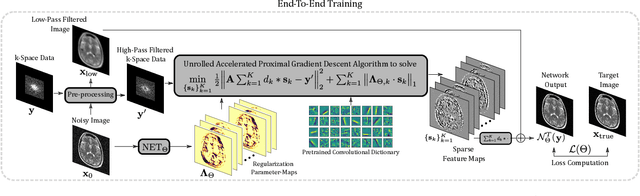
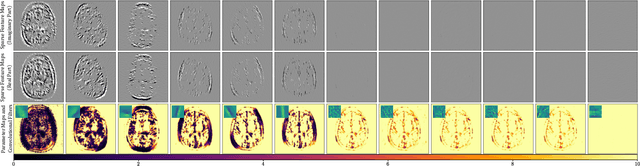
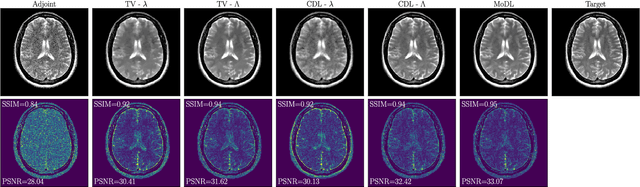
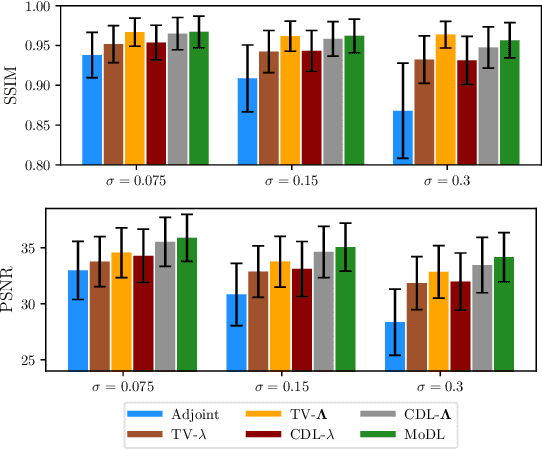
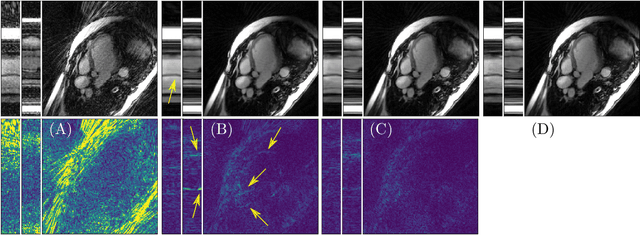
We propose an unrolled algorithm approach for learning spatially adaptive parameter maps in the framework of convolutional synthesis-based $\ell_1$ regularization. More precisely, we consider a family of pre-trained convolutional filters and estimate deeply parametrized spatially varying parameters applied to the sparse feature maps by means of unrolling a FISTA algorithm to solve the underlying sparse estimation problem. The proposed approach is evaluated for image reconstruction of low-field MRI and compared to spatially adaptive and non-adaptive analysis-type procedures relying on Total Variation regularization and to a well-established model-based deep learning approach. We show that the proposed approach produces visually and quantitatively comparable results with the latter approaches and at the same time remains highly interpretable. In particular, the inferred parameter maps quantify the local contribution of each filter in the reconstruction, which provides valuable insight into the algorithm mechanism and could potentially be used to discard unsuited filters.

Deep unrolling for learning optimal spatially varying regularisation parameters for Total Generalised Variation

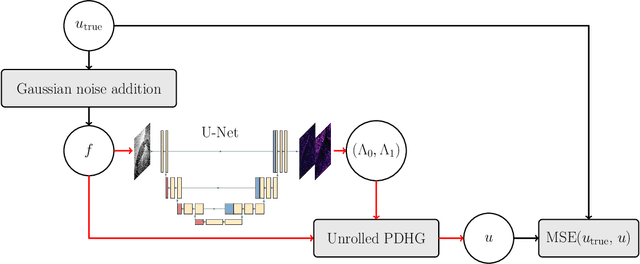
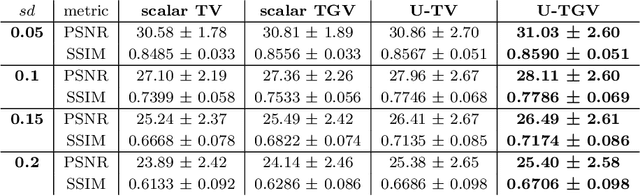
We extend a recently introduced deep unrolling framework for learning spatially varying regularisation parameters in inverse imaging problems to the case of Total Generalised Variation (TGV). The framework combines a deep convolutional neural network (CNN) inferring the two spatially varying TGV parameters with an unrolled algorithmic scheme that solves the corresponding variational problem. The two subnetworks are jointly trained end-to-end in a supervised fashion and as such the CNN learns to compute those parameters that drive the reconstructed images as close to the ground truth as possible. Numerical results in image denoising and MRI reconstruction show a significant qualitative and quantitative improvement compared to the best TGV scalar parameter case as well as to other approaches employing spatially varying parameters computed by unsupervised methods. We also observe that the inferred spatially varying parameter maps have a consistent structure near the image edges, asking for further theoretical investigations. In particular, the parameter that weighs the first-order TGV term has a triple-edge structure with alternating high-low-high values whereas the one that weighs the second-order term attains small values in a large neighbourhood around the edges.

MR imaging in the low-field: Leveraging the power of machine learning

Recent innovations in Magnetic Resonance Imaging (MRI) hardware and software have reignited interest in low-field ($<1\,\mathrm{T}$) and ultra-low-field MRI ($<0.1\,\mathrm{T}$). These technologies offer advantages such as lower power consumption, reduced specific absorption rate, reduced field-inhomogeneities, and cost-effectiveness, presenting a promising alternative for resource-limited and point-of-care settings. However, low-field MRI faces inherent challenges like reduced signal-to-noise ratio and therefore, potentially lower spatial resolution or longer scan times. This chapter examines the challenges and opportunities of low-field and ultra-low-field MRI, with a focus on the role of machine learning (ML) in overcoming these limitations. We provide an overview of deep neural networks and their application in enhancing low-field and ultra-low-field MRI performance. Specific ML-based solutions, including advanced image reconstruction, denoising, and super-resolution algorithms, are discussed. The chapter concludes by exploring how integrating ML with low-field MRI could expand its clinical applications and improve accessibility, potentially revolutionizing its use in diverse healthcare settings.

NoSENSE: Learned unrolled cardiac MRI reconstruction without explicit sensitivity maps

We present a novel learned image reconstruction method for accelerated cardiac MRI with multiple receiver coils based on deep convolutional neural networks (CNNs) and algorithm unrolling. In contrast to many existing learned MR image reconstruction techniques that necessitate coil-sensitivity map (CSM) estimation as a distinct network component, our proposed approach avoids explicit CSM estimation. Instead, it implicitly captures and learns to exploit the inter-coil relationships of the images. Our method consists of a series of novel learned image and k-space blocks with shared latent information and adaptation to the acquisition parameters by feature-wise modulation (FiLM), as well as coil-wise data-consistency (DC) blocks. Our method achieved PSNR values of 34.89 and 35.56 and SSIM values of 0.920 and 0.942 in the cine track and mapping track validation leaderboard of the MICCAI STACOM CMRxRecon Challenge, respectively, ranking 4th among different teams at the time of writing. Code will be made available at https://github.com/fzimmermann89/CMRxRecon

Quantitative MR Image Reconstruction using Parameter-Specific Dictionary Learning with Adaptive Dictionary-Size and Sparsity-Level Choice

Objective: We propose a method for the reconstruction of parameter-maps in Quantitative Magnetic Resonance Imaging (QMRI). Methods: Because different quantitative parameter-maps differ from each other in terms of local features, we propose a method where the employed dictionary learning (DL) and sparse coding (SC) algorithms automatically estimate the optimal dictionary-size and sparsity level separately for each parameter-map. We evaluated the method on a $T_1$-mapping QMRI problem in the brain using the BrainWeb data as well as in-vivo brain images acquired on an ultra-high field 7T scanner. We compared it to a model-based acceleration for parameter mapping (MAP) approach, other sparsity-based methods using total variation (TV), Wavelets (Wl) and Shearlets (Sh), and to a method which uses DL and SC to reconstruct qualitative images, followed by a non-linear (DL+Fit). Results: Our algorithm surpasses MAP, TV, Wl and Sh in terms of RMSE and PSNR. It yields better or comparable results to DL+Fit by additionally significantly accelerating the reconstruction by a factor of approximately seven. Conclusion: The proposed method outperforms the reported methods of comparison and yields accurate $T_1$-maps. Although presented for $T_1$-mapping in the brain, our method's structure is general and thus most probably also applicable for the the reconstruction of other quantitative parameters in other organs. Significance: From a clinical perspective, the obtained $T_1$-maps could be utilized to differentiate between healthy subjects and patients with Alzheimer's disease. From a technical perspective, the proposed unsupervised method could be employed to obtain ground-truth data for the development of data-driven methods based on supervised learning.+

PINQI: An End-to-End Physics-Informed Approach to Learned Quantitative MRI Reconstruction

Quantitative Magnetic Resonance Imaging (qMRI) enables the reproducible measurement of biophysical parameters in tissue. The challenge lies in solving a nonlinear, ill-posed inverse problem to obtain the desired tissue parameter maps from acquired raw data. While various learned and non-learned approaches have been proposed, the existing learned methods fail to fully exploit the prior knowledge about the underlying MR physics, i.e. the signal model and the acquisition model. In this paper, we propose PINQI, a novel qMRI reconstruction method that integrates the knowledge about the signal, acquisition model, and learned regularization into a single end-to-end trainable neural network. Our approach is based on unrolled alternating optimization, utilizing differentiable optimization blocks to solve inner linear and non-linear optimization tasks, as well as convolutional layers for regularization of the intermediate qualitative images and parameter maps. This design enables PINQI to leverage the advantages of both the signal model and learned regularization. We evaluate the performance of our proposed network by comparing it with recently published approaches in the context of highly undersampled $T_1$-mapping, using both a simulated brain dataset, as well as real scanner data acquired from a physical phantom and in-vivo data from healthy volunteers. The results demonstrate the superiority of our proposed solution over existing methods and highlight the effectiveness of our method in real-world scenarios.

Unrolled three-operator splitting for parameter-map learning in Low Dose X-ray CT reconstruction

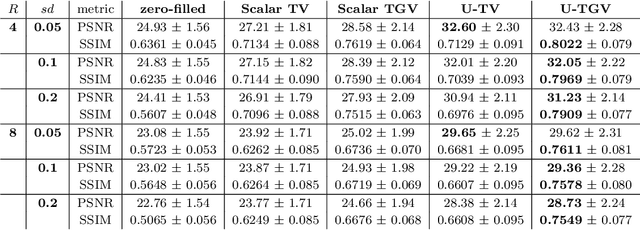
We propose a method for fast and automatic estimation of spatially dependent regularization maps for total variation-based (TV) tomography reconstruction. The estimation is based on two distinct sub-networks, with the first sub-network estimating the regularization parameter-map from the input data while the second one unrolling T iterations of the Primal-Dual Three-Operator Splitting (PD3O) algorithm. The latter approximately solves the corresponding TV-minimization problem incorporating the previously estimated regularization parameter-map. The overall network is then trained end-to-end in a supervised learning fashion using pairs of clean-corrupted data but crucially without the need of having access to labels for the optimal regularization parameter-maps.

Convolutional Dictionary Learning by End-To-End Training of Iterative Neural Networks

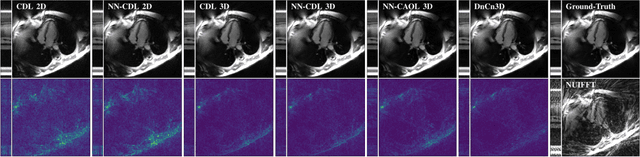
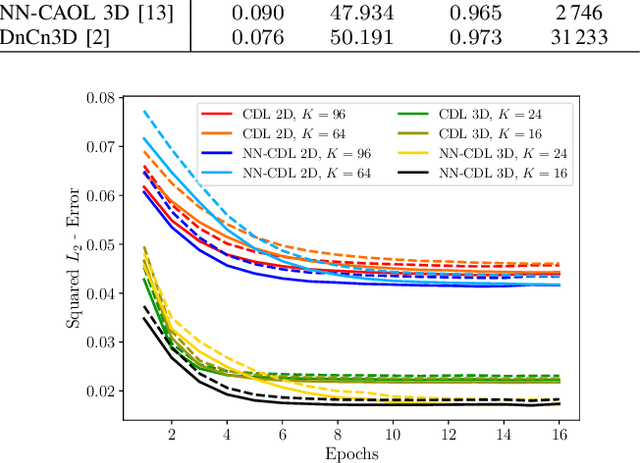
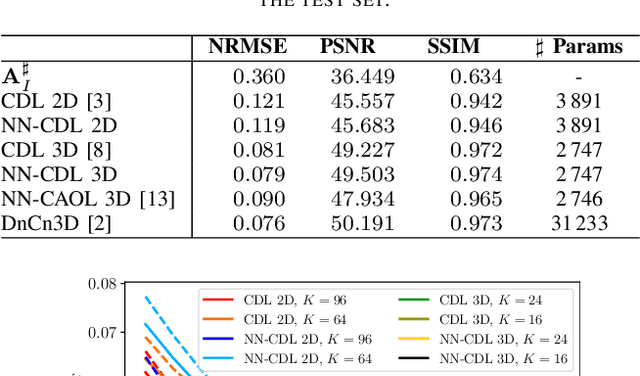
Sparsity-based methods have a long history in the field of signal processing and have been successfully applied to various image reconstruction problems. The involved sparsifying transformations or dictionaries are typically either pre-trained using a model which reflects the assumed properties of the signals or adaptively learned during the reconstruction - yielding so-called blind Compressed Sensing approaches. However, by doing so, the transforms are never explicitly trained in conjunction with the physical model which generates the signals. In addition, properly choosing the involved regularization parameters remains a challenging task. Another recently emerged training-paradigm for regularization methods is to use iterative neural networks (INNs) - also known as unrolled networks - which contain the physical model. In this work, we construct an INN which can be used as a supervised and physics-informed online convolutional dictionary learning algorithm. We evaluated the proposed approach by applying it to a realistic large-scale dynamic MR reconstruction problem and compared it to several other recently published works. We show that the proposed INN improves over two conventional model-agnostic training methods and yields competitive results also compared to a deep INN. Further, it does not require to choose the regularization parameters and - in contrast to deep INNs - each network component is entirely interpretable.

Convolutional Analysis Operator Learning by End-To-End Training of Iterative Neural Networks

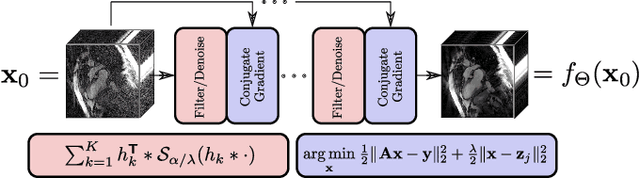
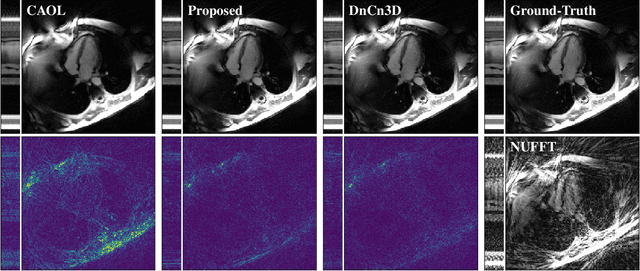
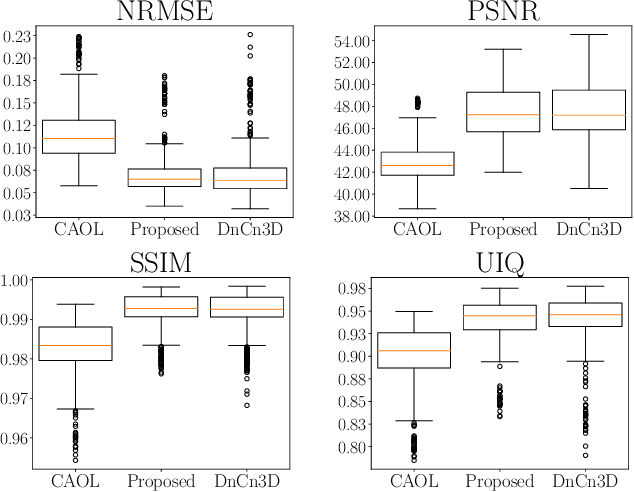
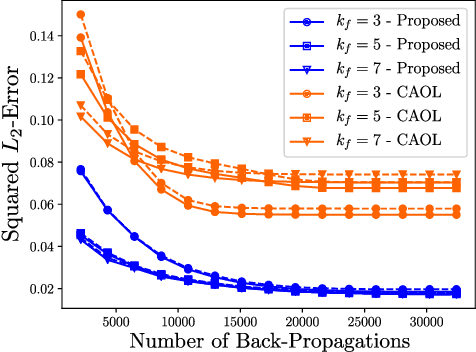
The concept of sparsity has been extensively applied for regularization in image reconstruction. Typically, sparsifying transforms are either pre-trained on ground-truth images or adaptively trained during the reconstruction. Thereby, learning algorithms are designed to minimize some target function which encodes the desired properties of the transform. However, this procedure ignores the subsequently employed reconstruction algorithm as well as the physical model which is responsible for the image formation process. Iterative neural networks - which contain the physical model - can overcome these issues. In this work, we demonstrate how convolutional sparsifying filters can be efficiently learned by end-to-end training of iterative neural networks. We evaluated our approach on a non-Cartesian 2D cardiac cine MRI example and show that the obtained filters are better suitable for the corresponding reconstruction algorithm than the ones obtained by decoupled pre-training.

An End-To-End-Trainable Iterative Network Architecture for Accelerated Radial Multi-Coil 2D Cine MR Image Reconstruction

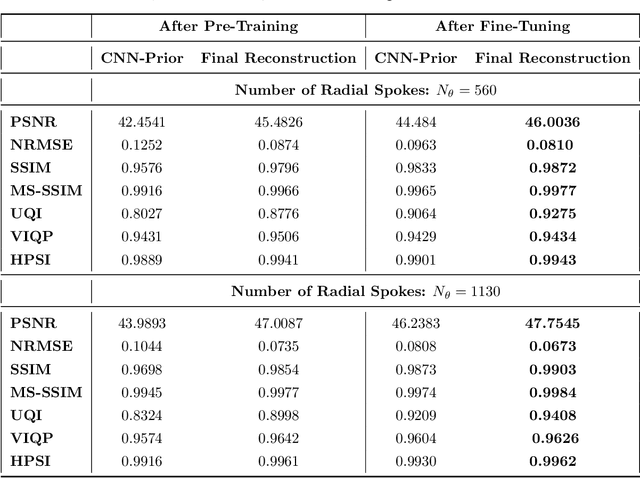
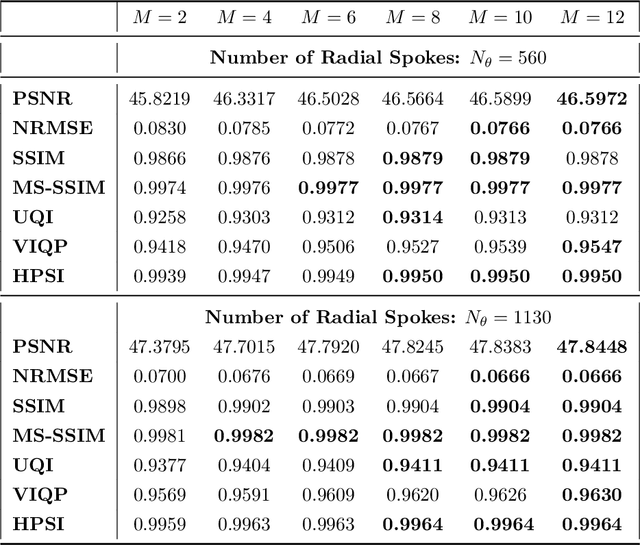
Purpose: Iterative Convolutional Neural Networks (CNNs) which resemble unrolled learned iterative schemes have shown to consistently deliver state-of-the-art results for image reconstruction problems across different imaging modalities. However, because these methodes include the forward model in the architecture, their applicability is often restricted to either relatively small reconstruction problems or to problems with operators which are computationally cheap to compute. As a consequence, they have so far not been applied to dynamic non-Cartesian multi-coil reconstruction problems. Methods: In this work, we propose a CNN-architecture for image reconstruction of accelerated 2D radial cine MRI with multiple receiver coils. The network is based on a computationally light CNN-component and a subsequent conjugate gradient (CG) method which can be jointly trained end-to-end using an efficient training strategy. We investigate the proposed training-strategy and compare our method to other well-known reconstruction techniques with learned and non-learned regularization methods. Results: Our proposed method outperforms all other methods based on non-learned regularization. Further, it performs similar or better than a CNN-based method employing a 3D U-Net and a method using adaptive dictionary learning. In addition, we empirically demonstrate that even by training the network with only iteration, it is possible to increase the length of the network at test time and further improve the results. Conclusions: End-to-end training allows to highly reduce the number of trainable parameters of and stabilize the reconstruction network. Further, because it is possible to change the length of the network at test time, the need to find a compromise between the complexity of the CNN-block and the number of iterations in each CG-block becomes irrelevant.