Variable Bregman Majorization-Minimization Algorithm and its Application to Dirichlet Maximum Likelihood Estimation

We propose a novel Bregman descent algorithm for minimizing a convex function that is expressed as the sum of a differentiable part (defined over an open set) and a possibly nonsmooth term. The approach, referred to as the Variable Bregman Majorization-Minimization (VBMM) algorithm, extends the Bregman Proximal Gradient method by allowing the Bregman function used in the divergence to adaptively vary at each iteration, provided it satisfies a majorizing condition on the objective function. This adaptive framework enables the algorithm to approximate the objective more precisely at each iteration, thereby allowing for accelerated convergence compared to the traditional Bregman Proximal Gradient descent. We establish the convergence of the VBMM algorithm to a minimizer under mild assumptions on the family of metrics used. Furthermore, we introduce a novel application of both the Bregman Proximal Gradient method and the VBMM algorithm to the estimation of the multidimensional parameters of a Dirichlet distribution through the maximization of its log-likelihood. Numerical experiments confirm that the VBMM algorithm outperforms existing approaches in terms of convergence speed.

Stability Bounds for the Unfolded Forward-Backward Algorithm

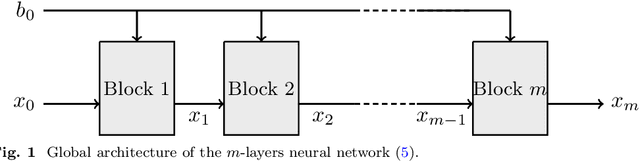
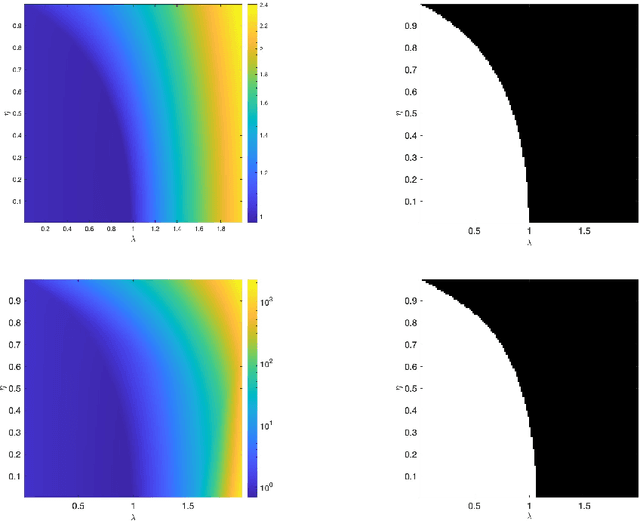
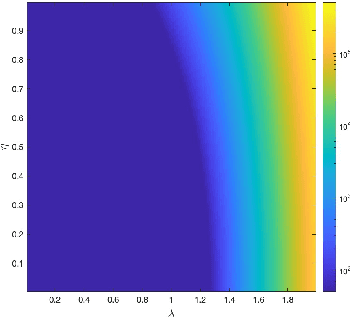
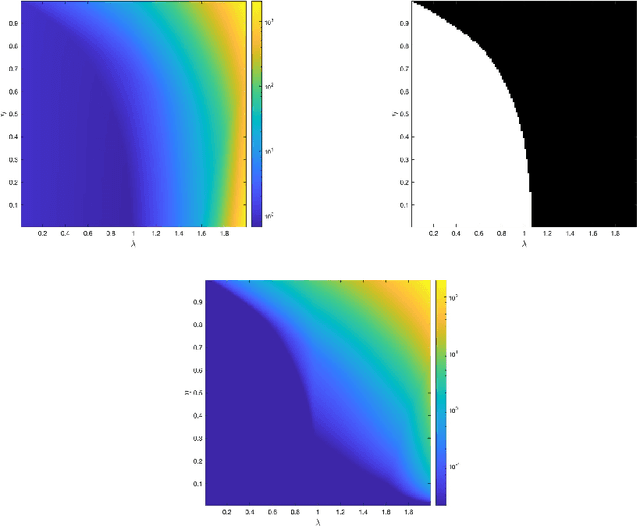
We consider a neural network architecture designed to solve inverse problems where the degradation operator is linear and known. This architecture is constructed by unrolling a forward-backward algorithm derived from the minimization of an objective function that combines a data-fidelity term, a Tikhonov-type regularization term, and a potentially nonsmooth convex penalty. The robustness of this inversion method to input perturbations is analyzed theoretically. Ensuring robustness complies with the principles of inverse problem theory, as it ensures both the continuity of the inversion method and the resilience to small noise - a critical property given the known vulnerability of deep neural networks to adversarial perturbations. A key novelty of our work lies in examining the robustness of the proposed network to perturbations in its bias, which represents the observed data in the inverse problem. Additionally, we provide numerical illustrations of the analytical Lipschitz bounds derived in our analysis.

UNEM: UNrolled Generalized EM for Transductive Few-Shot Learning

Transductive few-shot learning has recently triggered wide attention in computer vision. Yet, current methods introduce key hyper-parameters, which control the prediction statistics of the test batches, such as the level of class balance, affecting performances significantly. Such hyper-parameters are empirically grid-searched over validation data, and their configurations may vary substantially with the target dataset and pre-training model, making such empirical searches both sub-optimal and computationally intractable. In this work, we advocate and introduce the unrolling paradigm, also referred to as "learning to optimize", in the context of few-shot learning, thereby learning efficiently and effectively a set of optimized hyper-parameters. Specifically, we unroll a generalization of the ubiquitous Expectation-Maximization (EM) optimizer into a neural network architecture, mapping each of its iterates to a layer and learning a set of key hyper-parameters over validation data. Our unrolling approach covers various statistical feature distributions and pre-training paradigms, including recent foundational vision-language models and standard vision-only classifiers. We report comprehensive experiments, which cover a breadth of fine-grained downstream image classification tasks, showing significant gains brought by the proposed unrolled EM algorithm over iterative variants. The achieved improvements reach up to 10% and 7.5% on vision-only and vision-language benchmarks, respectively.

Primary liver cancer classification from routine tumour biopsy using weakly supervised deep learning

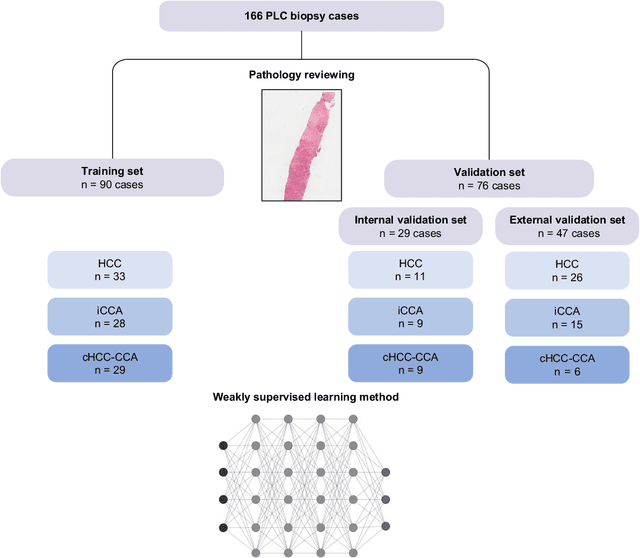
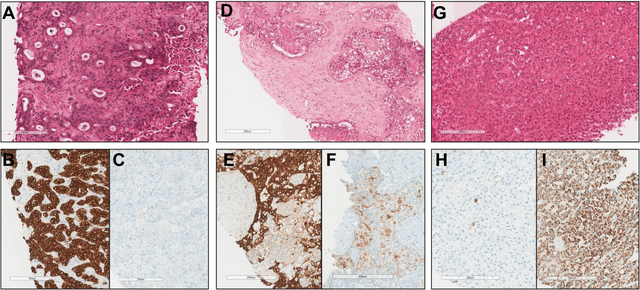
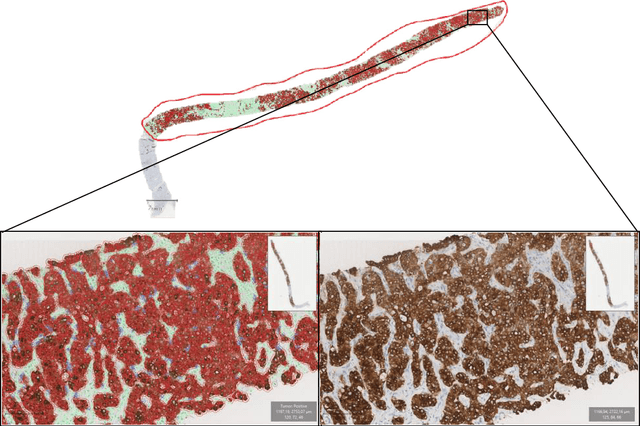
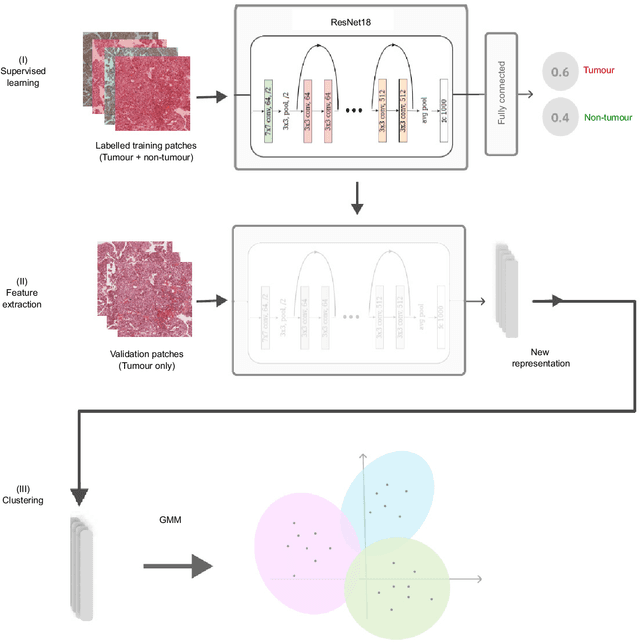
The diagnosis of primary liver cancers (PLCs) can be challenging, especially on biopsies and for combined hepatocellular-cholangiocarcinoma (cHCC-CCA). We automatically classified PLCs on routine-stained biopsies using a weakly supervised learning method. Weak tumour/non-tumour annotations served as labels for training a Resnet18 neural network, and the network's last convolutional layer was used to extract new tumour tile features. Without knowledge of the precise labels of the malignancies, we then applied an unsupervised clustering algorithm. Our model identified specific features of hepatocellular carcinoma (HCC) and intrahepatic cholangiocarcinoma (iCCA). Despite no specific features of cHCC-CCA being recognized, the identification of HCC and iCCA tiles within a slide could facilitate the diagnosis of primary liver cancers, particularly cHCC-CCA. Method and results: 166 PLC biopsies were divided into training, internal and external validation sets: 90, 29 and 47 samples. Two liver pathologists reviewed each whole-slide hematein eosin saffron (HES)-stained image (WSI). After annotating the tumour/non-tumour areas, 256x256 pixel tiles were extracted from the WSIs and used to train a ResNet18. The network was used to extract new tile features. An unsupervised clustering algorithm was then applied to the new tile features. In a two-cluster model, Clusters 0 and 1 contained mainly HCC and iCCA histological features. The diagnostic agreement between the pathological diagnosis and the model predictions in the internal and external validation sets was 100% (11/11) and 96% (25/26) for HCC and 78% (7/9) and 87% (13/15) for iCCA, respectively. For cHCC-CCA, we observed a highly variable proportion of tiles from each cluster (Cluster 0: 5-97%; Cluster 1: 2-94%).

Learning truly monotone operators with applications to nonlinear inverse problems

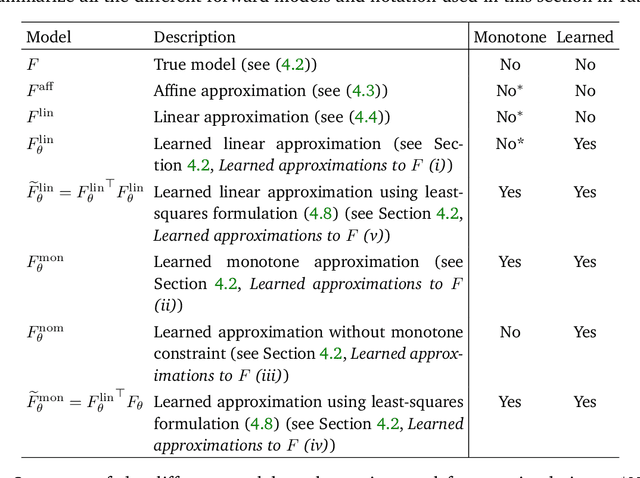
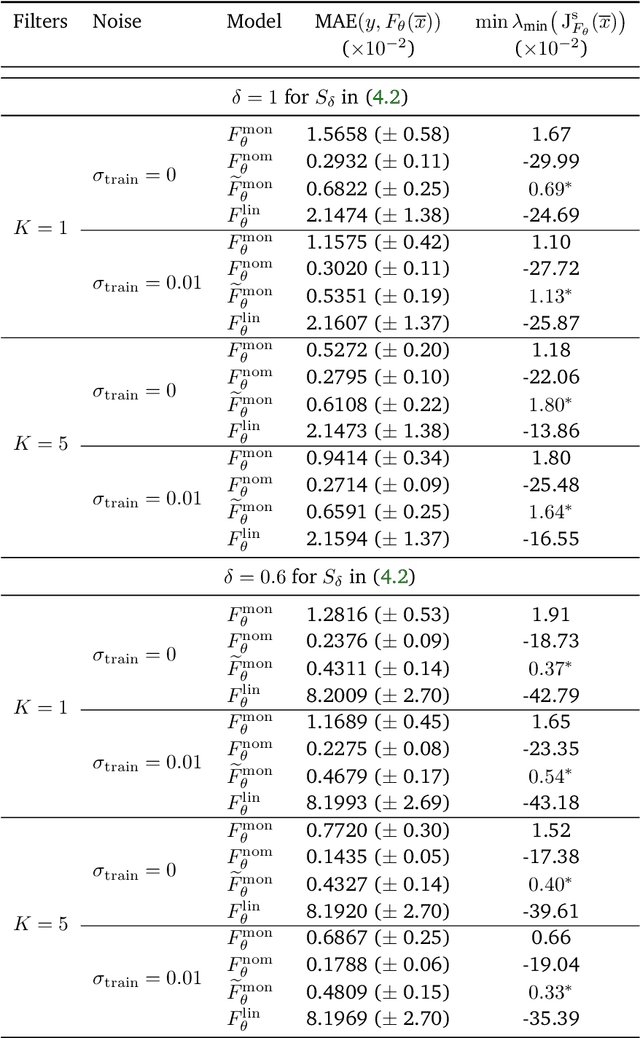
This article introduces a novel approach to learning monotone neural networks through a newly defined penalization loss. The proposed method is particularly effective in solving classes of variational problems, specifically monotone inclusion problems, commonly encountered in image processing tasks. The Forward-Backward-Forward (FBF) algorithm is employed to address these problems, offering a solution even when the Lipschitz constant of the neural network is unknown. Notably, the FBF algorithm provides convergence guarantees under the condition that the learned operator is monotone. Building on plug-and-play methodologies, our objective is to apply these newly learned operators to solving non-linear inverse problems. To achieve this, we initially formulate the problem as a variational inclusion problem. Subsequently, we train a monotone neural network to approximate an operator that may not inherently be monotone. Leveraging the FBF algorithm, we then show simulation examples where the non-linear inverse problem is successfully solved.

Convex Parameter Estimation of Perturbed Multivariate Generalized Gaussian Distributions

The multivariate generalized Gaussian distribution (MGGD), also known as the multivariate exponential power (MEP) distribution, is widely used in signal and image processing. However, estimating MGGD parameters, which is required in practical applications, still faces specific theoretical challenges. In particular, establishing convergence properties for the standard fixed-point approach when both the distribution mean and the scatter (or the precision) matrix are unknown is still an open problem. In robust estimation, imposing classical constraints on the precision matrix, such as sparsity, has been limited by the non-convexity of the resulting cost function. This paper tackles these issues from an optimization viewpoint by proposing a convex formulation with well-established convergence properties. We embed our analysis in a noisy scenario where robustness is induced by modelling multiplicative perturbations. The resulting framework is flexible as it combines a variety of regularizations for the precision matrix, the mean and model perturbations. This paper presents proof of the desired theoretical properties, specifies the conditions preserving these properties for different regularization choices and designs a general proximal primal-dual optimization strategy. The experiments show a more accurate precision and covariance matrix estimation with similar performance for the mean vector parameter compared to Tyler's M-estimator. In a high-dimensional setting, the proposed method outperforms the classical GLASSO, one of its robust extensions, and the regularized Tyler's estimator.

A Novel Variational Approach for Multiphoton Microscopy Image Restoration: from PSF Estimation to 3D Deconvolution

In multi-photon microscopy (MPM), a recent in-vivo fluorescence microscopy system, the task of image restoration can be decomposed into two interlinked inverse problems: firstly, the characterization of the Point Spread Function (PSF) and subsequently, the deconvolution (i.e., deblurring) to remove the PSF effect, and reduce noise. The acquired MPM image quality is critically affected by PSF blurring and intense noise. The PSF in MPM is highly spread in 3D and is not well characterized, presenting high variability with respect to the observed objects. This makes the restoration of MPM images challenging. Common PSF estimation methods in fluorescence microscopy, including MPM, involve capturing images of sub-resolution beads, followed by quantifying the resulting ellipsoidal 3D spot. In this work, we revisit this approach, coping with its inherent limitations in terms of accuracy and practicality. We estimate the PSF from the observation of relatively large beads (approximately 1$\mu$m in diameter). This goes through the formulation and resolution of an original non-convex minimization problem, for which we propose a proximal alternating method along with convergence guarantees. Following the PSF estimation step, we then introduce an innovative strategy to deal with the high level multiplicative noise degrading the acquisitions. We rely on a heteroscedastic noise model for which we estimate the parameters. We then solve a constrained optimization problem to restore the image, accounting for the estimated PSF and noise, while allowing a minimal hyper-parameter tuning. Theoretical guarantees are given for the restoration algorithm. These algorithmic contributions lead to an end-to-end pipeline for 3D image restoration in MPM, that we share as a publicly available Python software. We demonstrate its effectiveness through several experiments on both simulated and real data.

A transductive few-shot learning approach for classification of digital histopathological slides from liver cancer

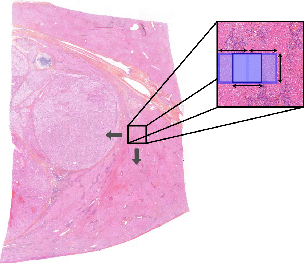
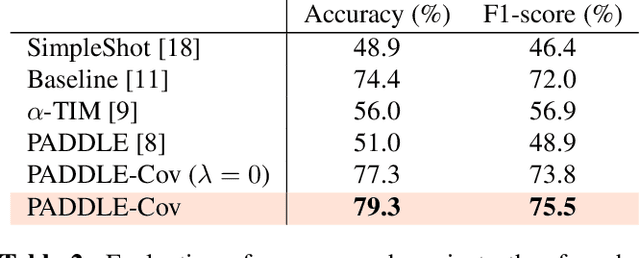
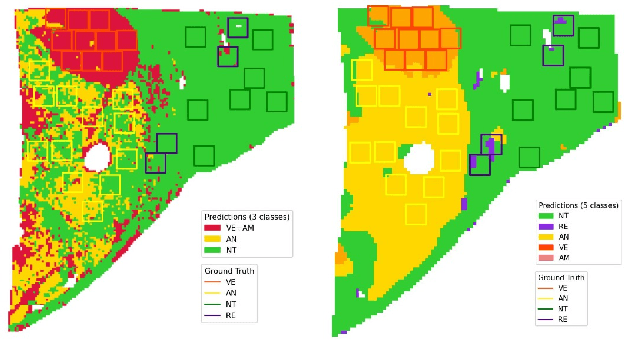
This paper presents a new approach for classifying 2D histopathology patches using few-shot learning. The method is designed to tackle a significant challenge in histopathology, which is the limited availability of labeled data. By applying a sliding window technique to histopathology slides, we illustrate the practical benefits of transductive learning (i.e., making joint predictions on patches) to achieve consistent and accurate classification. Our approach involves an optimization-based strategy that actively penalizes the prediction of a large number of distinct classes within each window. We conducted experiments on histopathological data to classify tissue classes in digital slides of liver cancer, specifically hepatocellular carcinoma. The initial results show the effectiveness of our method and its potential to enhance the process of automated cancer diagnosis and treatment, all while reducing the time and effort required for expert annotation.

Aggregated f-average Neural Network for Interpretable Ensembling

Ensemble learning leverages multiple models (i.e., weak learners) on a common machine learning task to enhance prediction performance. Basic ensembling approaches average the weak learners outputs, while more sophisticated ones stack a machine learning model in between the weak learners outputs and the final prediction. This work fuses both aforementioned frameworks. We introduce an aggregated f-average (AFA) shallow neural network which models and combines different types of averages to perform an optimal aggregation of the weak learners predictions. We emphasise its interpretable architecture and simple training strategy, and illustrate its good performance on the problem of few-shot class incremental learning.

Majorization-Minimization for sparse SVMs

Several decades ago, Support Vector Machines (SVMs) were introduced for performing binary classification tasks, under a supervised framework. Nowadays, they often outperform other supervised methods and remain one of the most popular approaches in the machine learning arena. In this work, we investigate the training of SVMs through a smooth sparse-promoting-regularized squared hinge loss minimization. This choice paves the way to the application of quick training methods built on majorization-minimization approaches, benefiting from the Lipschitz differentiabililty of the loss function. Moreover, the proposed approach allows us to handle sparsity-preserving regularizers promoting the selection of the most significant features, so enhancing the performance. Numerical tests and comparisons conducted on three different datasets demonstrate the good performance of the proposed methodology in terms of qualitative metrics (accuracy, precision, recall, and F 1 score) as well as computational cost.