Soil analysis with machine-learning-based processing of stepped-frequency GPR field measurements: Preliminary study

Ground Penetrating Radar (GPR) has been widely studied as a tool for extracting soil parameters relevant to agriculture and horticulture. When combined with Machine-Learning-based (ML) methods, high-resolution Stepped Frequency Countinuous Wave Radar (SFCW) measurements hold the promise to give cost effective access to depth resolved soil parameters, including at root-level depth. In a first step in this direction, we perform an extensive field survey with a tractor mounted SFCW GPR instrument. Using ML data processing we test the GPR instrument's capabilities to predict the apparent electrical conductivity (ECaR) as measured by a simultaneously recording Electromagnetic Induction (EMI) instrument. The large-scale field measurement campaign with 3472 co-registered and geo-located GPR and EMI data samples distributed over ~6600 square meters was performed on a golf course. The selected terrain benefits from a high surface homogeneity, but also features the challenge of only small, and hence hard to discern, variations in the measured soil parameter. Based on the quantitative results we suggest the use of nugget-to-sill ratio as a performance metric for the evaluation of end-to-end ML performance in the agricultural setting and discuss the limiting factors in the multi-sensor regression setting. The code is released as open source and available at https://opensource.silicon-austria.com/xuc/soil-analysis-machine-learning-stepped-frequency-gpr.

Majorization-Minimization for sparse SVMs

Several decades ago, Support Vector Machines (SVMs) were introduced for performing binary classification tasks, under a supervised framework. Nowadays, they often outperform other supervised methods and remain one of the most popular approaches in the machine learning arena. In this work, we investigate the training of SVMs through a smooth sparse-promoting-regularized squared hinge loss minimization. This choice paves the way to the application of quick training methods built on majorization-minimization approaches, benefiting from the Lipschitz differentiabililty of the loss function. Moreover, the proposed approach allows us to handle sparsity-preserving regularizers promoting the selection of the most significant features, so enhancing the performance. Numerical tests and comparisons conducted on three different datasets demonstrate the good performance of the proposed methodology in terms of qualitative metrics (accuracy, precision, recall, and F 1 score) as well as computational cost.

On the efficiency of Stochastic Quasi-Newton Methods for Deep Learning

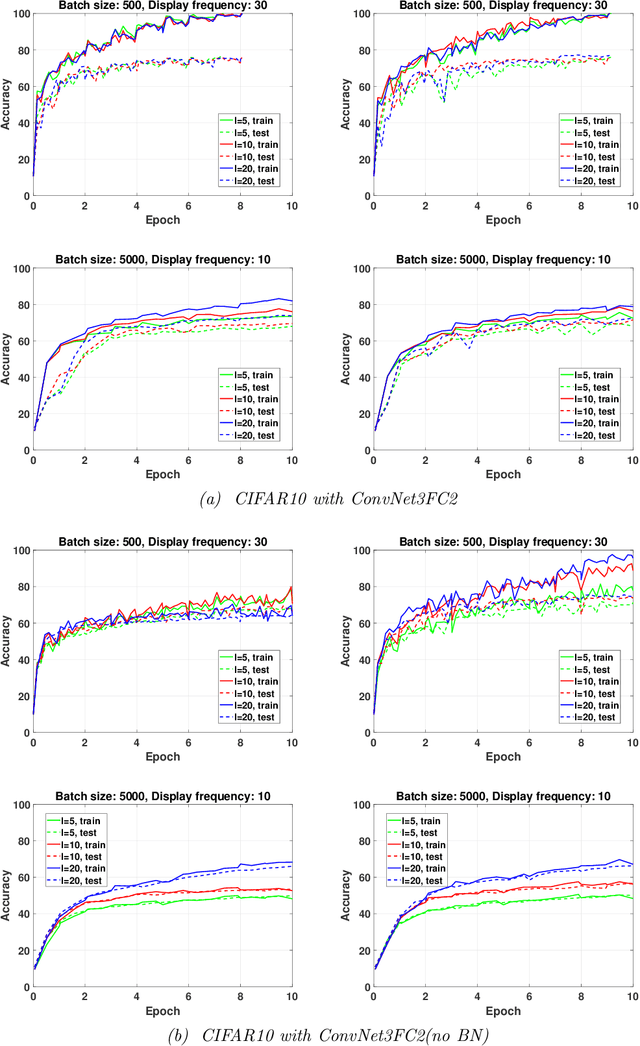
While first-order methods are popular for solving optimization problems that arise in large-scale deep learning problems, they come with some acute deficiencies. To diminish such shortcomings, there has been recent interest in applying second-order methods such as quasi-Newton based methods which construct Hessians approximations using only gradient information. The main focus of our work is to study the behaviour of stochastic quasi-Newton algorithms for training deep neural networks. We have analyzed the performance of two well-known quasi-Newton updates, the limited memory Broyden-Fletcher-Goldfarb-Shanno (BFGS) and the Symmetric Rank One (SR1). This study fills a gap concerning the real performance of both updates and analyzes whether more efficient training is obtained when using the more robust BFGS update or the cheaper SR1 formula which allows for indefinite Hessian approximations and thus can potentially help to better navigate the pathological saddle points present in the non-convex loss functions found in deep learning. We present and discuss the results of an extensive experimental study which includes the effect of batch normalization and network's architecture, the limited memory parameter, the batch size and the type of sampling strategy. we show that stochastic quasi-Newton optimizers are efficient and able to outperform in some instances the well-known first-order Adam optimizer run with the optimal combination of its numerous hyperparameters.