On the efficiency of Stochastic Quasi-Newton Methods for Deep Learning

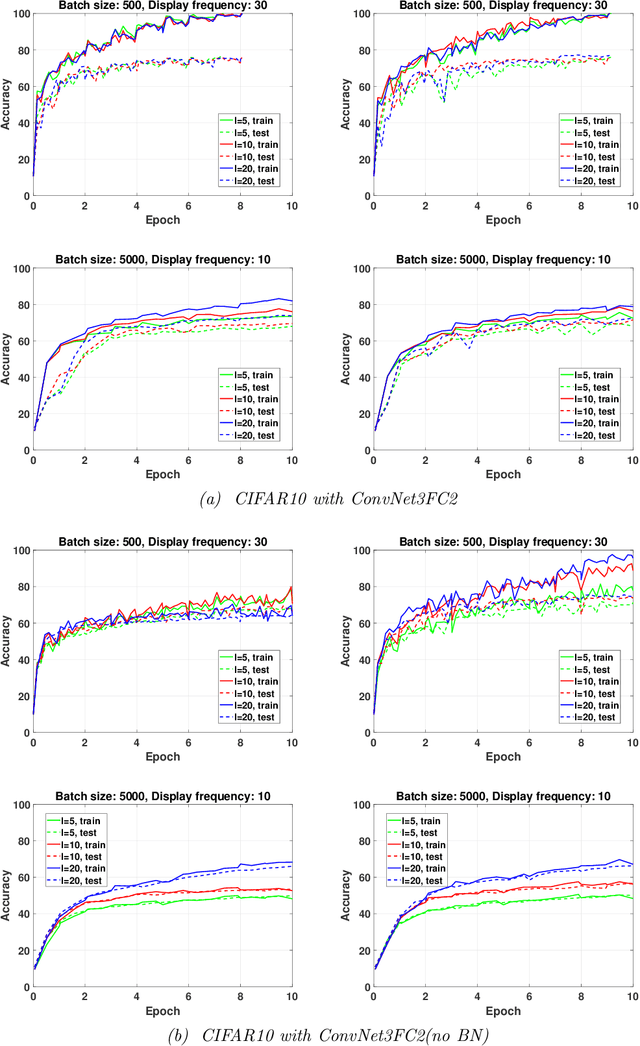
While first-order methods are popular for solving optimization problems that arise in large-scale deep learning problems, they come with some acute deficiencies. To diminish such shortcomings, there has been recent interest in applying second-order methods such as quasi-Newton based methods which construct Hessians approximations using only gradient information. The main focus of our work is to study the behaviour of stochastic quasi-Newton algorithms for training deep neural networks. We have analyzed the performance of two well-known quasi-Newton updates, the limited memory Broyden-Fletcher-Goldfarb-Shanno (BFGS) and the Symmetric Rank One (SR1). This study fills a gap concerning the real performance of both updates and analyzes whether more efficient training is obtained when using the more robust BFGS update or the cheaper SR1 formula which allows for indefinite Hessian approximations and thus can potentially help to better navigate the pathological saddle points present in the non-convex loss functions found in deep learning. We present and discuss the results of an extensive experimental study which includes the effect of batch normalization and network's architecture, the limited memory parameter, the batch size and the type of sampling strategy. we show that stochastic quasi-Newton optimizers are efficient and able to outperform in some instances the well-known first-order Adam optimizer run with the optimal combination of its numerous hyperparameters.