Primary liver cancer classification from routine tumour biopsy using weakly supervised deep learning

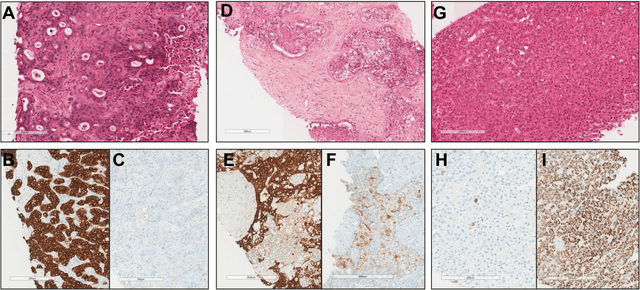
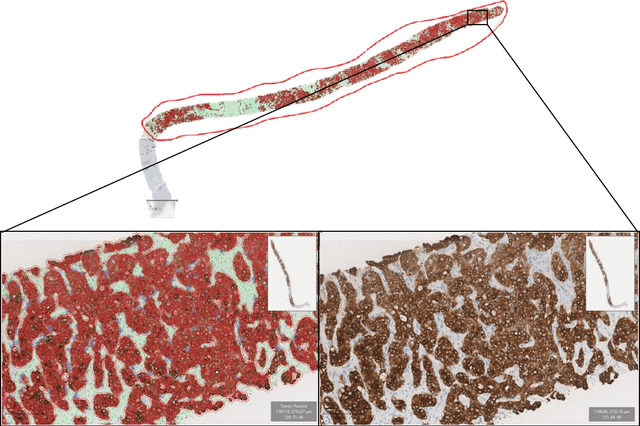
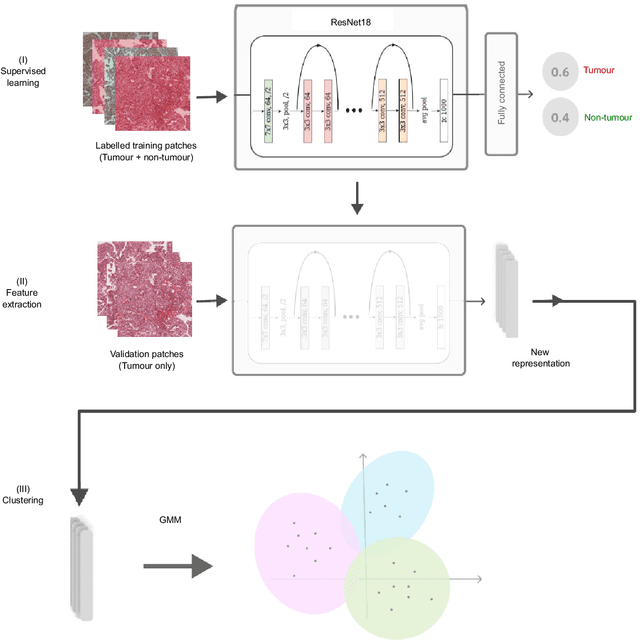
The diagnosis of primary liver cancers (PLCs) can be challenging, especially on biopsies and for combined hepatocellular-cholangiocarcinoma (cHCC-CCA). We automatically classified PLCs on routine-stained biopsies using a weakly supervised learning method. Weak tumour/non-tumour annotations served as labels for training a Resnet18 neural network, and the network's last convolutional layer was used to extract new tumour tile features. Without knowledge of the precise labels of the malignancies, we then applied an unsupervised clustering algorithm. Our model identified specific features of hepatocellular carcinoma (HCC) and intrahepatic cholangiocarcinoma (iCCA). Despite no specific features of cHCC-CCA being recognized, the identification of HCC and iCCA tiles within a slide could facilitate the diagnosis of primary liver cancers, particularly cHCC-CCA. Method and results: 166 PLC biopsies were divided into training, internal and external validation sets: 90, 29 and 47 samples. Two liver pathologists reviewed each whole-slide hematein eosin saffron (HES)-stained image (WSI). After annotating the tumour/non-tumour areas, 256x256 pixel tiles were extracted from the WSIs and used to train a ResNet18. The network was used to extract new tile features. An unsupervised clustering algorithm was then applied to the new tile features. In a two-cluster model, Clusters 0 and 1 contained mainly HCC and iCCA histological features. The diagnostic agreement between the pathological diagnosis and the model predictions in the internal and external validation sets was 100% (11/11) and 96% (25/26) for HCC and 78% (7/9) and 87% (13/15) for iCCA, respectively. For cHCC-CCA, we observed a highly variable proportion of tiles from each cluster (Cluster 0: 5-97%; Cluster 1: 2-94%).

Convex Parameter Estimation of Perturbed Multivariate Generalized Gaussian Distributions

The multivariate generalized Gaussian distribution (MGGD), also known as the multivariate exponential power (MEP) distribution, is widely used in signal and image processing. However, estimating MGGD parameters, which is required in practical applications, still faces specific theoretical challenges. In particular, establishing convergence properties for the standard fixed-point approach when both the distribution mean and the scatter (or the precision) matrix are unknown is still an open problem. In robust estimation, imposing classical constraints on the precision matrix, such as sparsity, has been limited by the non-convexity of the resulting cost function. This paper tackles these issues from an optimization viewpoint by proposing a convex formulation with well-established convergence properties. We embed our analysis in a noisy scenario where robustness is induced by modelling multiplicative perturbations. The resulting framework is flexible as it combines a variety of regularizations for the precision matrix, the mean and model perturbations. This paper presents proof of the desired theoretical properties, specifies the conditions preserving these properties for different regularization choices and designs a general proximal primal-dual optimization strategy. The experiments show a more accurate precision and covariance matrix estimation with similar performance for the mean vector parameter compared to Tyler's M-estimator. In a high-dimensional setting, the proposed method outperforms the classical GLASSO, one of its robust extensions, and the regularized Tyler's estimator.

Coupled Feature Learning for Multimodal Medical Image Fusion

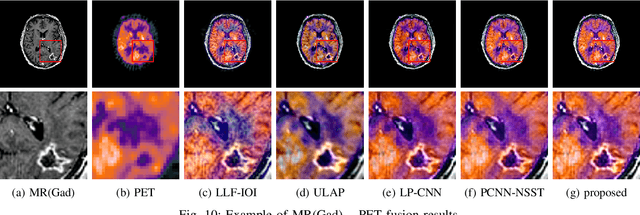
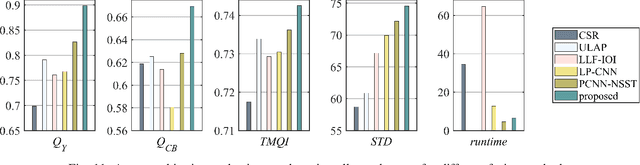
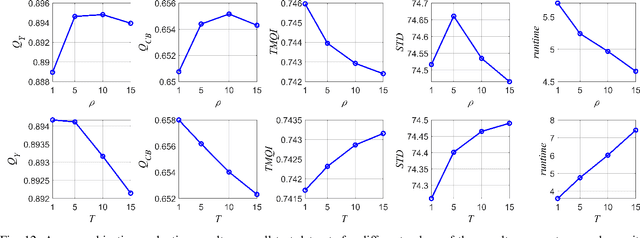
Multimodal image fusion aims to combine relevant information from images acquired with different sensors. In medical imaging, fused images play an essential role in both standard and automated diagnosis. In this paper, we propose a novel multimodal image fusion method based on coupled dictionary learning. The proposed method is general and can be employed for different medical imaging modalities. Unlike many current medical fusion methods, the proposed approach does not suffer from intensity attenuation nor loss of critical information. Specifically, the images to be fused are decomposed into coupled and independent components estimated using sparse representations with identical supports and a Pearson correlation constraint, respectively. An alternating minimization algorithm is designed to solve the resulting optimization problem. The final fusion step uses the max-absolute-value rule. Experiments are conducted using various pairs of multimodal inputs, including real MR-CT and MR-PET images. The resulting performance and execution times show the competitiveness of the proposed method in comparison with state-of-the-art medical image fusion methods.