Robust Activity Detection for Massive Random Access

Massive machine-type communications (mMTC) are fundamental to the Internet of Things (IoT) framework in future wireless networks, involving the connection of a vast number of devices with sporadic transmission patterns. Traditional device activity detection (AD) methods are typically developed for Gaussian noise, but their performance may deteriorate when these conditions are not met, particularly in the presence of heavy-tailed impulsive noise. In this paper, we propose robust statistical techniques for AD that do not rely on the Gaussian assumption and replace the Gaussian loss function with robust loss functions that can effectively mitigate the impact of heavy-tailed noise and outliers. First, we prove that the coordinate-wise (conditional) objective function is geodesically convex and derive a fixed-point (FP) algorithm for minimizing it, along with convergence guarantees. Building on the FP algorithm, we propose two robust algorithms for solving the full (unconditional) objective function: a coordinate-wise optimization algorithm (RCWO) and a greedy covariance learning-based matching pursuit algorithm (RCL-MP). Numerical experiments demonstrate that the proposed methods significantly outperform existing algorithms in scenarios with non-Gaussian noise, achieving higher detection accuracy and robustness.

SINR Maximizing Distributionally Robust Adaptive Beamforming

This paper addresses the robust adaptive beamforming (RAB) problem via the worst-case signal-to-interference-plus-noise ratio (SINR) maximization over distributional uncertainty sets for the random interference-plus-noise covariance (INC) matrix and desired signal steering vector. Our study explores two distinct uncertainty sets for the INC matrix and three for the steering vector. The uncertainty sets of the INC matrix account for the support and the positive semidefinite (PSD) mean of the distribution, as well as a similarity constraint on the mean. The uncertainty sets for the steering vector consist of the constraints on the first- and second-order moments of its associated probability distribution. The RAB problem is formulated as the minimization of the worst-case expected value of the SINR denominator over any distribution within the uncertainty set of the INC matrix, subject to the condition that the expected value of the numerator is greater than or equal to one for every distribution within the uncertainty set of the steering vector. By leveraging the strong duality of linear conic programming, this RAB problem is reformulated as a quadratic matrix inequality problem. Subsequently, it is addressed by iteratively solving a sequence of linear matrix inequality relaxation problems, incorporating a penalty term for the rank-one PSD matrix constraint. We further analyze the convergence of the iterative algorithm. The proposed robust beamforming approach is validated through simulation examples, which illustrate improved performance in terms of the array output SINR.

AI-Empowered Integrated Sensing and Communications

Integrating sensing and communication (ISAC) can help overcome the challenges of limited spectrum and expensive hardware, leading to improved energy and cost efficiency. While full cooperation between sensing and communication can result in significant performance gains, achieving optimal performance requires efficient designs of unified waveforms and beamformers for joint sensing and communication. Sophisticated statistical signal processing and multi-objective optimization techniques are necessary to balance the competing design requirements of joint sensing and communication tasks. Since model-based analytical approaches may be suboptimal or overly complex, deep learning emerges as a powerful tool for developing data-driven signal processing algorithms, particularly when optimal algorithms are unknown or when known algorithms are too complex for real-time implementation. Unified waveform and beamformer design problems for ISAC fall into this category, where fundamental design trade-offs exist between sensing and communication performance metrics, and the underlying models may be inadequate or incomplete. This article explores the application of artificial intelligence (AI) in ISAC designs to enhance efficiency and reduce complexity. We emphasize the integration benefits through AI-driven ISAC designs, prioritizing the development of unified waveforms, constellations, and beamforming strategies for both sensing and communication. To illustrate the practical potential of AI-driven ISAC, we present two case studies on waveform and beamforming design, demonstrating how unsupervised learning and neural network-based optimization can effectively balance performance, complexity, and implementation constraints.

Pilot Contamination Aware Transformer for Downlink Power Control in Cell-Free Massive MIMO Networks

Learning-based downlink power control in cell-free massive multiple-input multiple-output (CFmMIMO) systems offers a promising alternative to conventional iterative optimization algorithms, which are computationally intensive due to online iterative steps. Existing learning-based methods, however, often fail to exploit the intrinsic structure of channel data and neglect pilot allocation information, leading to suboptimal performance, especially in large-scale networks with many users. This paper introduces the pilot contamination-aware power control (PAPC) transformer neural network, a novel approach that integrates pilot allocation data into the network, effectively handling pilot contamination scenarios. PAPC employs the attention mechanism with a custom masking technique to utilize structural information and pilot data. The architecture includes tailored preprocessing and post-processing stages for efficient feature extraction and adherence to power constraints. Trained in an unsupervised learning framework, PAPC is evaluated against the accelerated proximal gradient (APG) algorithm, showing comparable spectral efficiency fairness performance while significantly improving computational efficiency. Simulations demonstrate PAPC's superior performance over fully connected networks (FCNs) that lack pilot information, its scalability to large-scale CFmMIMO networks, and its computational efficiency improvement over APG. Additionally, by employing padding techniques, PAPC adapts to the dynamically varying number of users without retraining.

AdaBoost-Based Efficient Channel Estimation and Data Detection in One-Bit Massive MIMO

The use of one-bit analog-to-digital converter (ADC) has been considered as a viable alternative to high resolution counterparts in realizing and commercializing massive multiple-input multiple-output (MIMO) systems. However, the issue of discarding the amplitude information by one-bit quantizers has to be compensated. Thus, carefully tailored methods need to be developed for one-bit channel estimation and data detection as the conventional ones cannot be used. To address these issues, the problems of one-bit channel estimation and data detection for MIMO orthogonal frequency division multiplexing (OFDM) system that operates over uncorrelated frequency selective channels are investigated here. We first develop channel estimators that exploit Gaussian discriminant analysis (GDA) classifier and approximated versions of it as the so-called weak classifiers in an adaptive boosting (AdaBoost) approach. Particularly, the combination of the approximated GDA classifiers with AdaBoost offers the benefit of scalability with the linear order of computations, which is critical in massive MIMO-OFDM systems. We then take advantage of the same idea for proposing the data detectors. Numerical results validate the efficiency of the proposed channel estimators and data detectors compared to other methods. They show comparable/better performance to that of the state-of-the-art methods, but require dramatically lower computational complexities and run times.

An Efficient Approximate Method for Online Convolutional Dictionary Learning

Most existing convolutional dictionary learning (CDL) algorithms are based on batch learning, where the dictionary filters and the convolutional sparse representations are optimized in an alternating manner using a training dataset. When large training datasets are used, batch CDL algorithms become prohibitively memory-intensive. An online-learning technique is used to reduce the memory requirements of CDL by optimizing the dictionary incrementally after finding the sparse representations of each training sample. Nevertheless, learning large dictionaries using the existing online CDL (OCDL) algorithms remains highly computationally expensive. In this paper, we present a novel approximate OCDL method that incorporates sparse decomposition of the training samples. The resulting optimization problems are addressed using the alternating direction method of multipliers. Extensive experimental evaluations using several image datasets show that the proposed method substantially reduces computational costs while preserving the effectiveness of the state-of-the-art OCDL algorithms.

Twenty-Five Years of Advances in Beamforming: From Convex and Nonconvex Optimization to Learning Techniques

Beamforming is a signal processing technique to steer, shape, and focus an electromagnetic wave using an array of sensors toward a desired direction. It has been used in several engineering applications such as radar, sonar, acoustics, astronomy, seismology, medical imaging, and communications. With the advances in multi-antenna technologies largely for radar and communications, there has been a great interest on beamformer design mostly relying on convex/nonconvex optimization. Recently, machine learning is being leveraged for obtaining attractive solutions to more complex beamforming problems. This article captures the evolution of beamforming in the last twenty-five years from convex-to-nonconvex optimization and optimization-to-learning approaches. It provides a glimpse of this important signal processing technique into a variety of transmit-receive architectures, propagation zones, paths, and conventional/emerging applications.

Robust Adaptive Beamforming via Worst-Case SINR Maximization with Nonconvex Uncertainty Sets

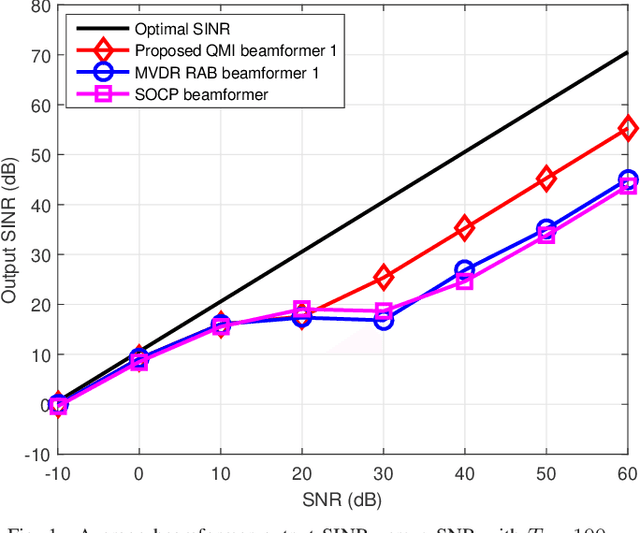
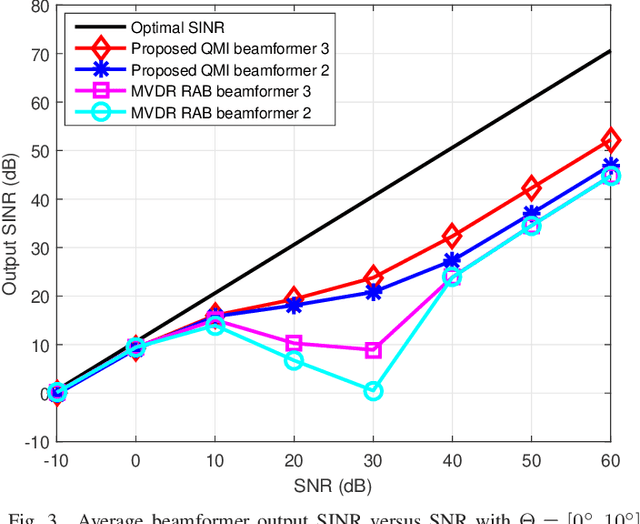
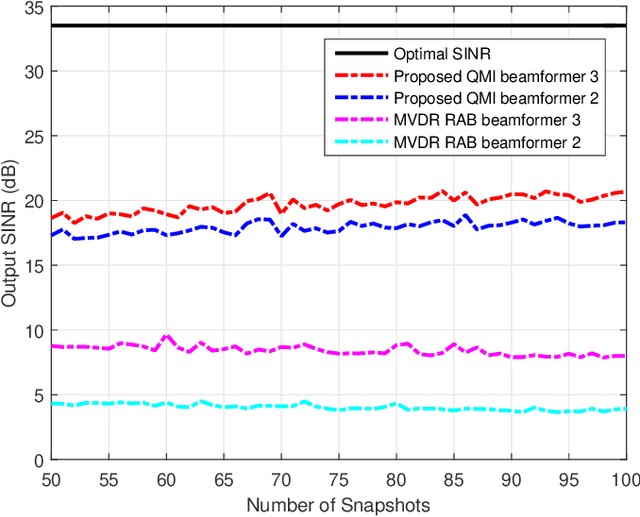
This paper considers a formulation of the robust adaptive beamforming (RAB) problem based on worst-case signal-to-interference-plus-noise ratio (SINR) maximization with a nonconvex uncertainty set for the steering vectors. The uncertainty set consists of a similarity constraint and a (nonconvex) double-sided ball constraint. The worst-case SINR maximization problem is turned into a quadratic matrix inequality (QMI) problem using the strong duality of semidefinite programming. Then a linear matrix inequality (LMI) relaxation for the QMI problem is proposed, with an additional valid linear constraint. Necessary and sufficient conditions for the tightened LMI relaxation problem to have a rank-one solution are established. When the tightened LMI relaxation problem still has a high-rank solution, the LMI relaxation problem is further restricted to become a bilinear matrix inequality (BLMI) problem. We then propose an iterative algorithm to solve the BLMI problem that finds an optimal/suboptimal solution for the original RAB problem by solving the BLMI formulations. To validate our results, simulation examples are presented to demonstrate the improved array output SINR of the proposed robust beamformer.

Convolutional Simultaneous Sparse Approximation with Applications to RGB-NIR Image Fusion

Simultaneous sparse approximation (SSA) seeks to represent a set of dependent signals using sparse vectors with identical supports. The SSA model has been used in various signal and image processing applications involving multiple correlated input signals. In this paper, we propose algorithms for convolutional SSA (CSSA) based on the alternating direction method of multipliers. Specifically, we address the CSSA problem with different sparsity structures and the convolutional feature learning problem in multimodal data/signals based on the SSA model. We evaluate the proposed algorithms by applying them to multimodal and multifocus image fusion problems.

Graph Neural Network Sensitivity Under Probabilistic Error Model

Graph convolutional networks (GCNs) can successfully learn the graph signal representation by graph convolution. The graph convolution depends on the graph filter, which contains the topological dependency of data and propagates data features. However, the estimation errors in the propagation matrix (e.g., the adjacency matrix) can have a significant impact on graph filters and GCNs. In this paper, we study the effect of a probabilistic graph error model on the performance of the GCNs. We prove that the adjacency matrix under the error model is bounded by a function of graph size and error probability. We further analytically specify the upper bound of a normalized adjacency matrix with self-loop added. Finally, we illustrate the error bounds by running experiments on a synthetic dataset and study the sensitivity of a simple GCN under this probabilistic error model on accuracy.