Optimal Robust Adaptive Beamforming for a General-Rank Signal Model via Equivalence of Maximin and Minimax SINR Problems

The globally optimal robust adaptive beamforming (RAB) solution is studied for worst-case signal-to-interference-plus-noise ratio (SINR) maximization (the maximin SINR problem) under convex and closed uncertainty sets for the desired signal covariance and interference-plus-noise covariance (INC) matrices, considering a general-rank signal model. First, the corresponding minimax SINR problem is reformulated as a convex optimization problem. In particular, this problem becomes a semidefinite programming (SDP) problem when the uncertainty sets can be represented by finitely many linear matrix inequality constraints. It is then shown that, for a general-rank signal model, the maximin and minimax SINR problems are equivalent when the uncertainty sets are convex and closed, in the sense that they share the same optimal value and the same set of optimal solutions. The requirement of closedness is weaker than the compactness assumption previously used to establish the equivalence between minimax and maximin SINR problems for the rank-one signal model, a state-of-the-art result reported approximately two decades ago. Consequently, an optimal solution to the minimax SINR problem is also globally optimal for the maximin SINR problem, and this solution can be obtained by solving the equivalent SDP of the minimax problem in a single step. In contrast, existing iterative approximation algorithms for the maximin SINR problem yield only locally optimal solutions. Simulation results demonstrate that these approximation algorithms return suboptimal values that can be strictly smaller than the optimal value of the minimax problem, and that the beamformer output SINR obtained via the minimax formulation is higher than that achieved by beamformers derived from the maximin problem using approximation algorithms.

SINR Maximizing Distributionally Robust Adaptive Beamforming

This paper addresses the robust adaptive beamforming (RAB) problem via the worst-case signal-to-interference-plus-noise ratio (SINR) maximization over distributional uncertainty sets for the random interference-plus-noise covariance (INC) matrix and desired signal steering vector. Our study explores two distinct uncertainty sets for the INC matrix and three for the steering vector. The uncertainty sets of the INC matrix account for the support and the positive semidefinite (PSD) mean of the distribution, as well as a similarity constraint on the mean. The uncertainty sets for the steering vector consist of the constraints on the first- and second-order moments of its associated probability distribution. The RAB problem is formulated as the minimization of the worst-case expected value of the SINR denominator over any distribution within the uncertainty set of the INC matrix, subject to the condition that the expected value of the numerator is greater than or equal to one for every distribution within the uncertainty set of the steering vector. By leveraging the strong duality of linear conic programming, this RAB problem is reformulated as a quadratic matrix inequality problem. Subsequently, it is addressed by iteratively solving a sequence of linear matrix inequality relaxation problems, incorporating a penalty term for the rank-one PSD matrix constraint. We further analyze the convergence of the iterative algorithm. The proposed robust beamforming approach is validated through simulation examples, which illustrate improved performance in terms of the array output SINR.

Robust Adaptive Beamforming via Worst-Case SINR Maximization with Nonconvex Uncertainty Sets

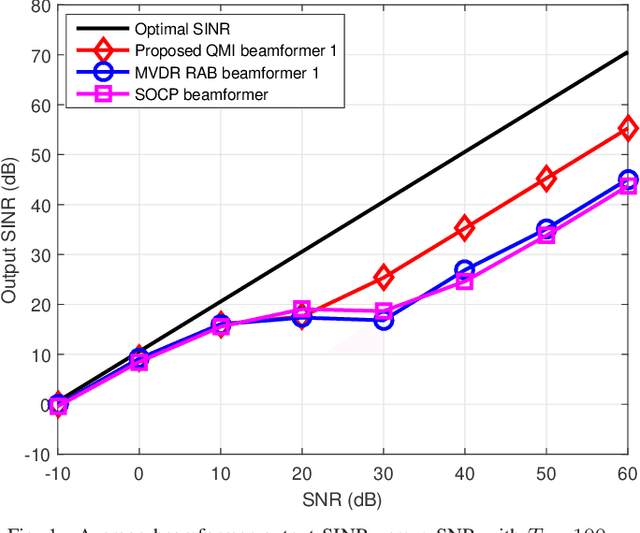
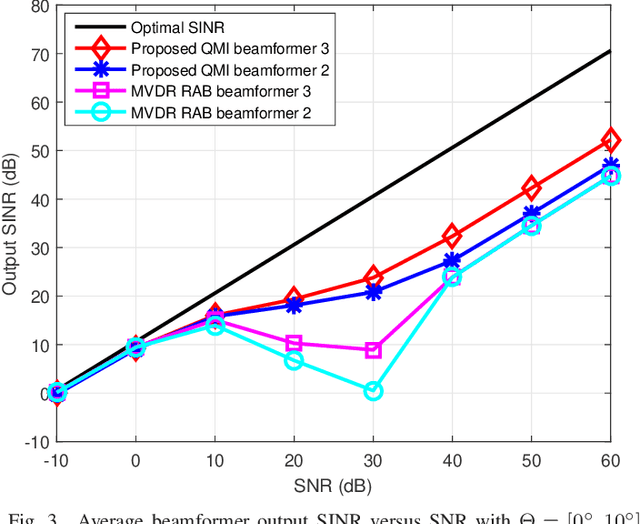
This paper considers a formulation of the robust adaptive beamforming (RAB) problem based on worst-case signal-to-interference-plus-noise ratio (SINR) maximization with a nonconvex uncertainty set for the steering vectors. The uncertainty set consists of a similarity constraint and a (nonconvex) double-sided ball constraint. The worst-case SINR maximization problem is turned into a quadratic matrix inequality (QMI) problem using the strong duality of semidefinite programming. Then a linear matrix inequality (LMI) relaxation for the QMI problem is proposed, with an additional valid linear constraint. Necessary and sufficient conditions for the tightened LMI relaxation problem to have a rank-one solution are established. When the tightened LMI relaxation problem still has a high-rank solution, the LMI relaxation problem is further restricted to become a bilinear matrix inequality (BLMI) problem. We then propose an iterative algorithm to solve the BLMI problem that finds an optimal/suboptimal solution for the original RAB problem by solving the BLMI formulations. To validate our results, simulation examples are presented to demonstrate the improved array output SINR of the proposed robust beamformer.

Robust Adaptive Beamforming Maximizing the Worst-Case SINR over Distributional Uncertainty Sets for Random INC Matrix and Signal Steering Vector

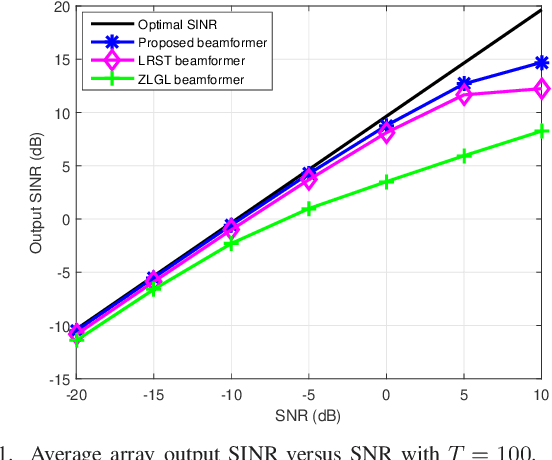
The robust adaptive beamforming (RAB) problem is considered via the worst-case signal-to-interference-plus-noise ratio (SINR) maximization over distributional uncertainty sets for the random interference-plus-noise covariance (INC) matrix and desired signal steering vector. The distributional uncertainty set of the INC matrix accounts for the support and the positive semidefinite (PSD) mean of the distribution, and a similarity constraint on the mean. The distributional uncertainty set for the steering vector consists of the constraints on the known first- and second-order moments. The RAB problem is formulated as a minimization of the worst-case expected value of the SINR denominator achieved by any distribution, subject to the expected value of the numerator being greater than or equal to one for each distribution. Resorting to the strong duality of linear conic programming, such a RAB problem is rewritten as a quadratic matrix inequality problem. It is then tackled by iteratively solving a sequence of linear matrix inequality relaxation problems with the penalty term on the rank-one PSD matrix constraint. To validate the results, simulation examples are presented, and they demonstrate the improved performance of the proposed robust beamformer in terms of the array output SINR.

Enhanced Robust Adaptive Beamforming Designs for General-Rank Signal Model via an Induced Norm of Matrix Errors

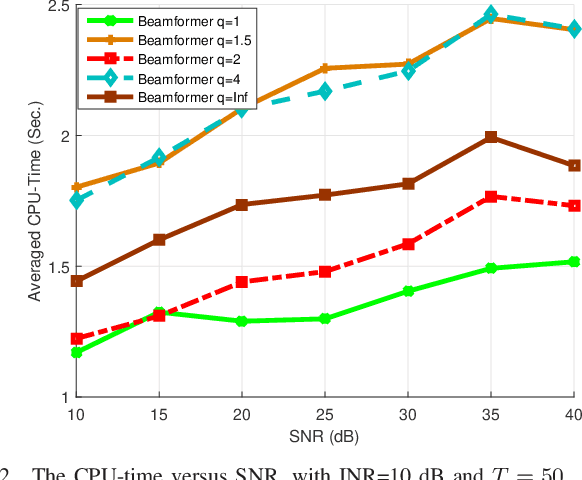
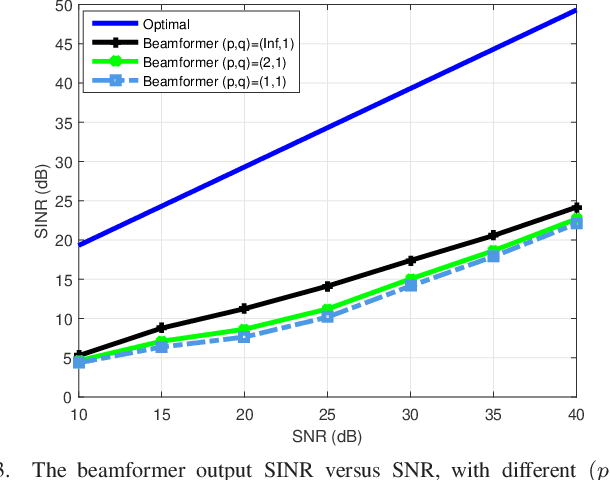
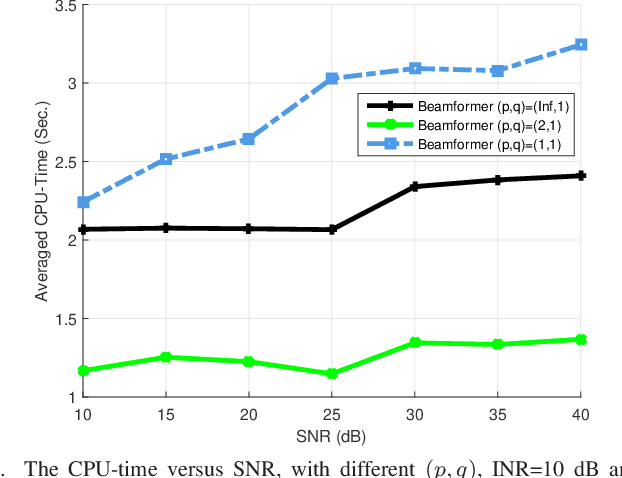
The robust adaptive beamforming (RAB) problem for general-rank signal model with an uncertainty set defined through a matrix induced norm is considered. The worst-case signal-to-interference-plus-noise ratio (SINR) maximization RAB problem is formulated by decomposing the presumed covariance of the desired signal into a product between a matrix and its Hermitian, and putting an error term into the matrix and its Hermitian. In the literature, the norm of the matrix errors often is the Frobenius norm in the maximization problem. Herein, the closed-form optimal value for a minimization problem of the least-squares residual over the matrix errors with an induced $l_{p,q}$-norm constraint is first derived. Then, the worst-case SINR maximization problem is reformulated into the maximization of the difference between an $l_2$-norm function and a $l_q$-norm function, subject to a convex quadratic constraint. It is shown that for any $q$ in the set of rational numbers greater than or equal to one, the maximization problem can be approximated by a sequence of second-order cone programming (SOCP) problems, with the ascent optimal values. The resultant beamvector for some $q$ in the set, corresponding to the maximal actual array output SINR, is treated as the best candidate such that the RAB design is improved the most. In addition, a generalized RAB problem of maximizing the difference between an $l_p$-norm function and an $l_q$-norm function subject to the convex quadratic constraint is studied, and the actual array output SINR is further enhanced by properly selecting $p$ and $q$. Simulation examples are presented to demonstrate the improved performance of the robust beamformers for certain matrix induced $l_{p,q}$-norms, in terms of the actual array output SINR and the CPU-time for the sequential SOCP approximation algorithm.