Enhanced Robust Adaptive Beamforming Designs for General-Rank Signal Model via an Induced Norm of Matrix Errors
Paper and Code
Mar 24, 2021
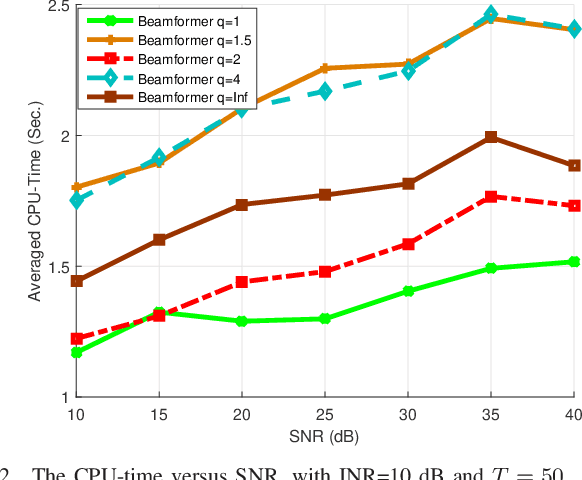
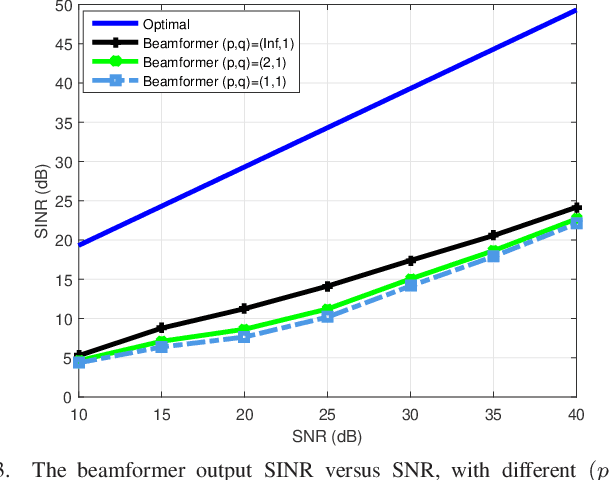
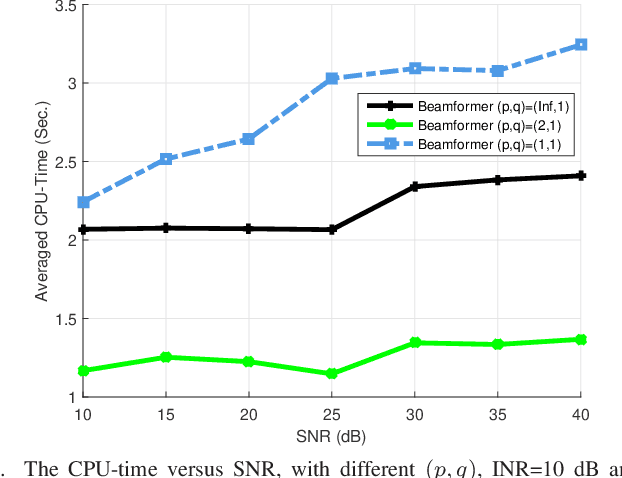
The robust adaptive beamforming (RAB) problem for general-rank signal model with an uncertainty set defined through a matrix induced norm is considered. The worst-case signal-to-interference-plus-noise ratio (SINR) maximization RAB problem is formulated by decomposing the presumed covariance of the desired signal into a product between a matrix and its Hermitian, and putting an error term into the matrix and its Hermitian. In the literature, the norm of the matrix errors often is the Frobenius norm in the maximization problem. Herein, the closed-form optimal value for a minimization problem of the least-squares residual over the matrix errors with an induced $l_{p,q}$-norm constraint is first derived. Then, the worst-case SINR maximization problem is reformulated into the maximization of the difference between an $l_2$-norm function and a $l_q$-norm function, subject to a convex quadratic constraint. It is shown that for any $q$ in the set of rational numbers greater than or equal to one, the maximization problem can be approximated by a sequence of second-order cone programming (SOCP) problems, with the ascent optimal values. The resultant beamvector for some $q$ in the set, corresponding to the maximal actual array output SINR, is treated as the best candidate such that the RAB design is improved the most. In addition, a generalized RAB problem of maximizing the difference between an $l_p$-norm function and an $l_q$-norm function subject to the convex quadratic constraint is studied, and the actual array output SINR is further enhanced by properly selecting $p$ and $q$. Simulation examples are presented to demonstrate the improved performance of the robust beamformers for certain matrix induced $l_{p,q}$-norms, in terms of the actual array output SINR and the CPU-time for the sequential SOCP approximation algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge