Robust Adaptive Beamforming via Worst-Case SINR Maximization with Nonconvex Uncertainty Sets
Paper and Code
Jun 13, 2022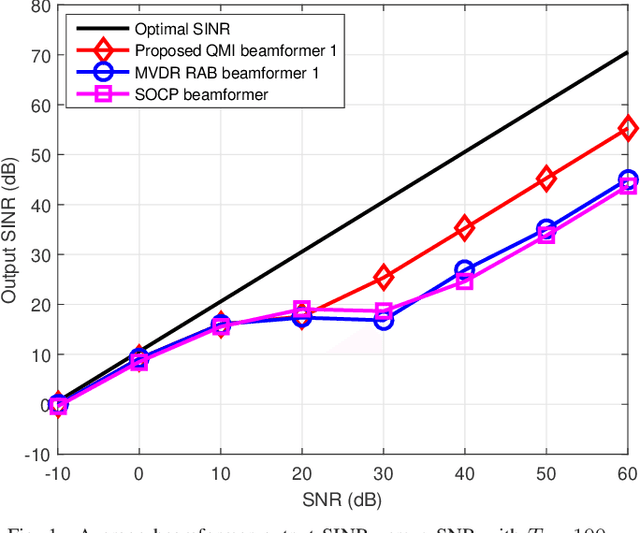

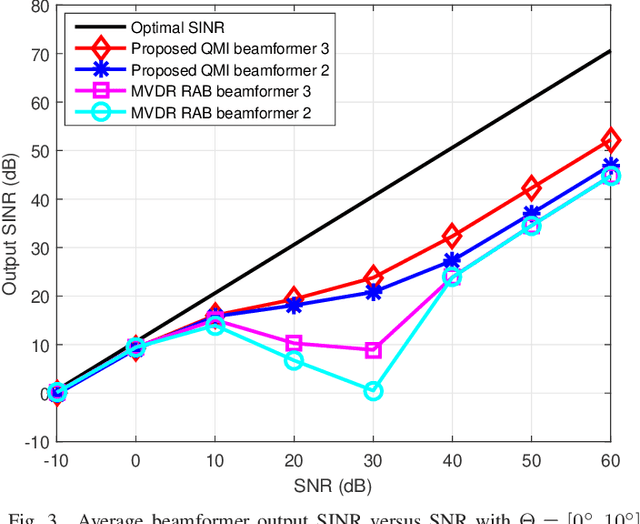
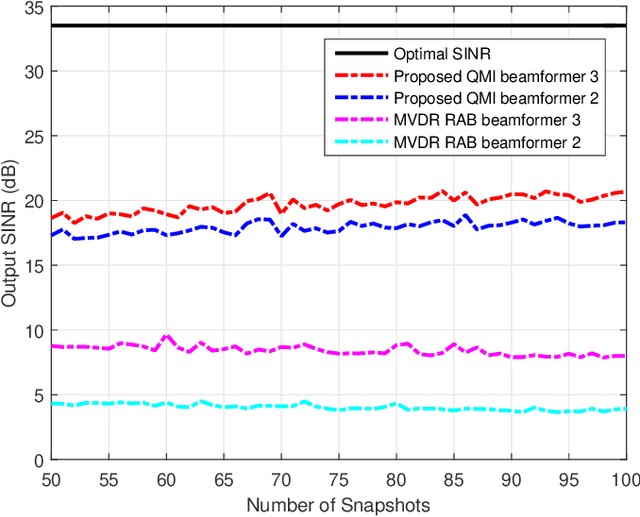
This paper considers a formulation of the robust adaptive beamforming (RAB) problem based on worst-case signal-to-interference-plus-noise ratio (SINR) maximization with a nonconvex uncertainty set for the steering vectors. The uncertainty set consists of a similarity constraint and a (nonconvex) double-sided ball constraint. The worst-case SINR maximization problem is turned into a quadratic matrix inequality (QMI) problem using the strong duality of semidefinite programming. Then a linear matrix inequality (LMI) relaxation for the QMI problem is proposed, with an additional valid linear constraint. Necessary and sufficient conditions for the tightened LMI relaxation problem to have a rank-one solution are established. When the tightened LMI relaxation problem still has a high-rank solution, the LMI relaxation problem is further restricted to become a bilinear matrix inequality (BLMI) problem. We then propose an iterative algorithm to solve the BLMI problem that finds an optimal/suboptimal solution for the original RAB problem by solving the BLMI formulations. To validate our results, simulation examples are presented to demonstrate the improved array output SINR of the proposed robust beamformer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge