Robust Adaptive Beamforming Maximizing the Worst-Case SINR over Distributional Uncertainty Sets for Random INC Matrix and Signal Steering Vector
Paper and Code
Oct 16, 2021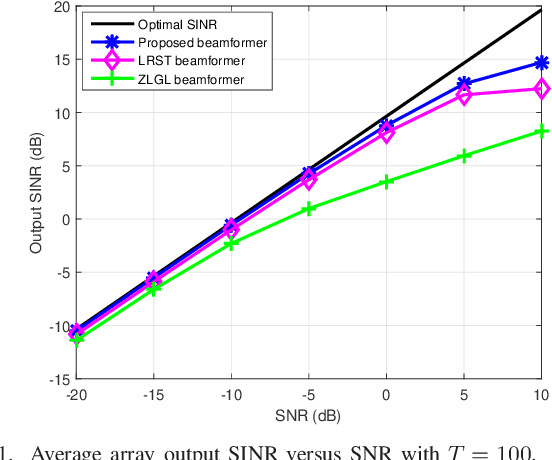

The robust adaptive beamforming (RAB) problem is considered via the worst-case signal-to-interference-plus-noise ratio (SINR) maximization over distributional uncertainty sets for the random interference-plus-noise covariance (INC) matrix and desired signal steering vector. The distributional uncertainty set of the INC matrix accounts for the support and the positive semidefinite (PSD) mean of the distribution, and a similarity constraint on the mean. The distributional uncertainty set for the steering vector consists of the constraints on the known first- and second-order moments. The RAB problem is formulated as a minimization of the worst-case expected value of the SINR denominator achieved by any distribution, subject to the expected value of the numerator being greater than or equal to one for each distribution. Resorting to the strong duality of linear conic programming, such a RAB problem is rewritten as a quadratic matrix inequality problem. It is then tackled by iteratively solving a sequence of linear matrix inequality relaxation problems with the penalty term on the rank-one PSD matrix constraint. To validate the results, simulation examples are presented, and they demonstrate the improved performance of the proposed robust beamformer in terms of the array output SINR.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge