Elliptical Wishart distributions: information geometry, maximum likelihood estimator, performance analysis and statistical learning

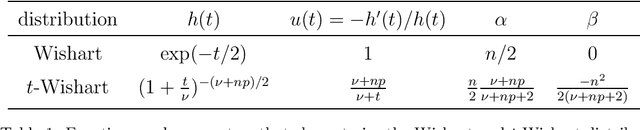
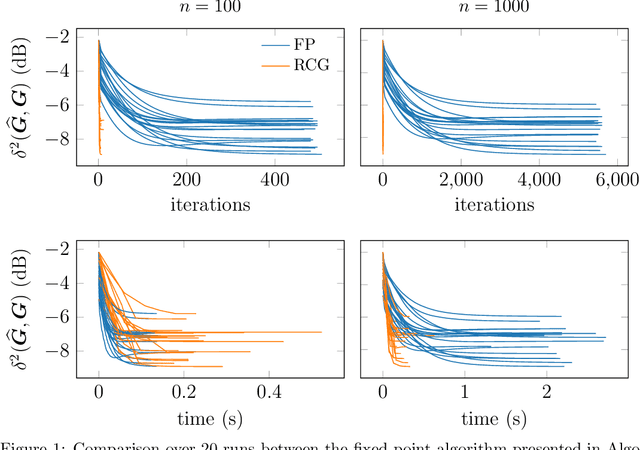
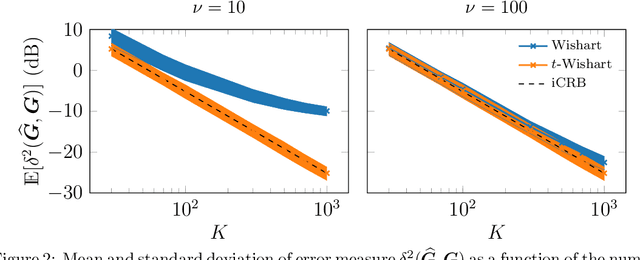
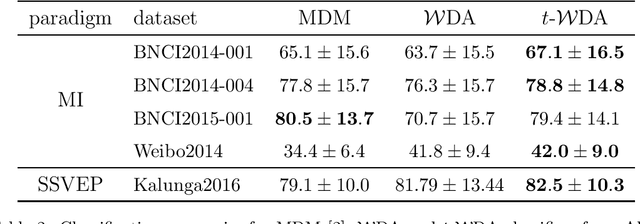
This paper deals with Elliptical Wishart distributions - which generalize the Wishart distribution - in the context of signal processing and machine learning. Two algorithms to compute the maximum likelihood estimator (MLE) are proposed: a fixed point algorithm and a Riemannian optimization method based on the derived information geometry of Elliptical Wishart distributions. The existence and uniqueness of the MLE are characterized as well as the convergence of both estimation algorithms. Statistical properties of the MLE are also investigated such as consistency, asymptotic normality and an intrinsic version of Fisher efficiency. On the statistical learning side, novel classification and clustering methods are designed. For the $t$-Wishart distribution, the performance of the MLE and statistical learning algorithms are evaluated on both simulated and real EEG and hyperspectral data, showcasing the interest of our proposed methods.

Random matrix theory improved Fréchet mean of symmetric positive definite matrices

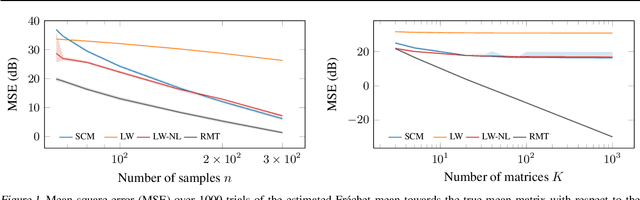
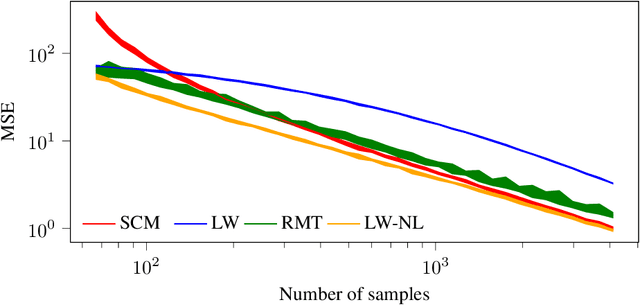
In this study, we consider the realm of covariance matrices in machine learning, particularly focusing on computing Fr\'echet means on the manifold of symmetric positive definite matrices, commonly referred to as Karcher or geometric means. Such means are leveraged in numerous machine-learning tasks. Relying on advanced statistical tools, we introduce a random matrix theory-based method that estimates Fr\'echet means, which is particularly beneficial when dealing with low sample support and a high number of matrices to average. Our experimental evaluation, involving both synthetic and real-world EEG and hyperspectral datasets, shows that we largely outperform state-of-the-art methods.

Sparse PCA with False Discovery Rate Controlled Variable Selection

Sparse principal component analysis (PCA) aims at mapping large dimensional data to a linear subspace of lower dimension. By imposing loading vectors to be sparse, it performs the double duty of dimension reduction and variable selection. Sparse PCA algorithms are usually expressed as a trade-off between explained variance and sparsity of the loading vectors (i.e., number of selected variables). As a high explained variance is not necessarily synonymous with relevant information, these methods are prone to select irrelevant variables. To overcome this issue, we propose an alternative formulation of sparse PCA driven by the false discovery rate (FDR). We then leverage the Terminating-Random Experiments (T-Rex) selector to automatically determine an FDR-controlled support of the loading vectors. A major advantage of the resulting T-Rex PCA is that no sparsity parameter tuning is required. Numerical experiments and a stock market data example demonstrate a significant performance improvement.

Convex Parameter Estimation of Perturbed Multivariate Generalized Gaussian Distributions

The multivariate generalized Gaussian distribution (MGGD), also known as the multivariate exponential power (MEP) distribution, is widely used in signal and image processing. However, estimating MGGD parameters, which is required in practical applications, still faces specific theoretical challenges. In particular, establishing convergence properties for the standard fixed-point approach when both the distribution mean and the scatter (or the precision) matrix are unknown is still an open problem. In robust estimation, imposing classical constraints on the precision matrix, such as sparsity, has been limited by the non-convexity of the resulting cost function. This paper tackles these issues from an optimization viewpoint by proposing a convex formulation with well-established convergence properties. We embed our analysis in a noisy scenario where robustness is induced by modelling multiplicative perturbations. The resulting framework is flexible as it combines a variety of regularizations for the precision matrix, the mean and model perturbations. This paper presents proof of the desired theoretical properties, specifies the conditions preserving these properties for different regularization choices and designs a general proximal primal-dual optimization strategy. The experiments show a more accurate precision and covariance matrix estimation with similar performance for the mean vector parameter compared to Tyler's M-estimator. In a high-dimensional setting, the proposed method outperforms the classical GLASSO, one of its robust extensions, and the regularized Tyler's estimator.

Choosing the parameter of the Fermat distance: navigating geometry and noise

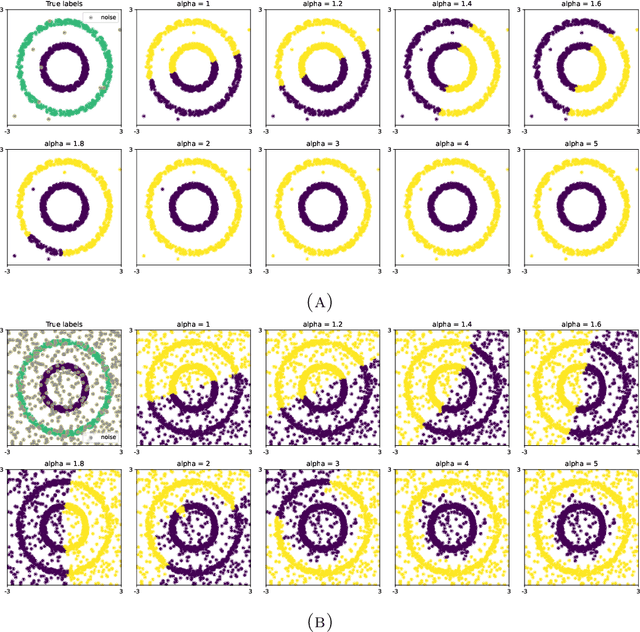
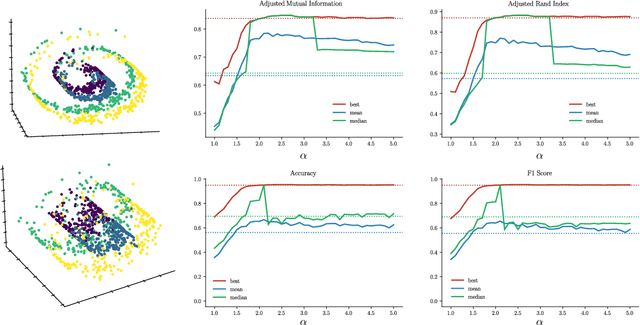
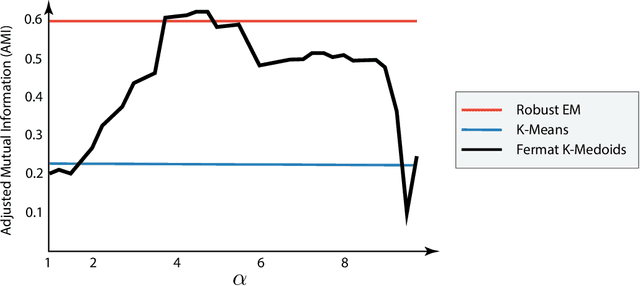
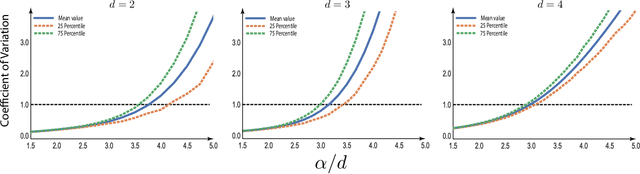
The Fermat distance has been recently established as a useful tool for machine learning tasks when a natural distance is not directly available to the practitioner or to improve the results given by Euclidean distances by exploding the geometrical and statistical properties of the dataset. This distance depends on a parameter $\alpha$ that greatly impacts the performance of subsequent tasks. Ideally, the value of $\alpha$ should be large enough to navigate the geometric intricacies inherent to the problem. At the same, it should remain restrained enough to sidestep any deleterious ramifications stemming from noise during the process of distance estimation. We study both theoretically and through simulations how to select this parameter.

A Robust and Flexible EM Algorithm for Mixtures of Elliptical Distributions with Missing Data

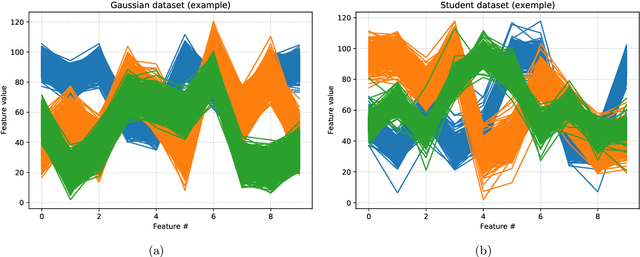
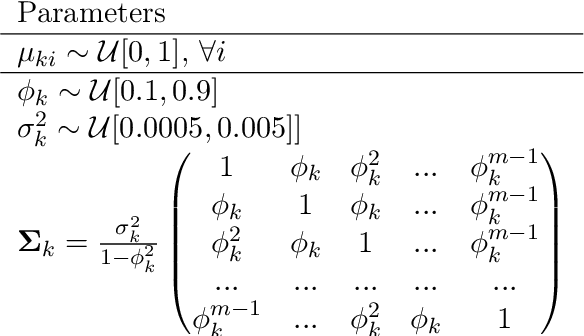
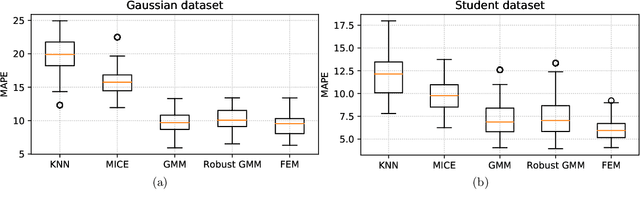
This paper tackles the problem of missing data imputation for noisy and non-Gaussian data. A classical imputation method, the Expectation Maximization (EM) algorithm for Gaussian mixture models, has shown interesting properties when compared to other popular approaches such as those based on k-nearest neighbors or on multiple imputations by chained equations. However, Gaussian mixture models are known to be not robust to heterogeneous data, which can lead to poor estimation performance when the data is contaminated by outliers or come from a non-Gaussian distributions. To overcome this issue, a new expectation maximization algorithm is investigated for mixtures of elliptical distributions with the nice property of handling potential missing data. The complete-data likelihood associated with mixtures of elliptical distributions is well adapted to the EM framework thanks to its conditional distribution, which is shown to be a Student distribution. Experimental results on synthetic data demonstrate that the proposed algorithm is robust to outliers and can be used with non-Gaussian data. Furthermore, experiments conducted on real-world datasets show that this algorithm is very competitive when compared to other classical imputation methods.

Robust classification with flexible discriminant analysis in heterogeneous data

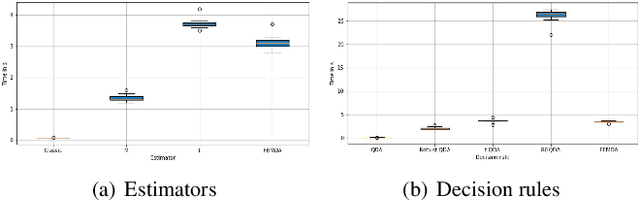
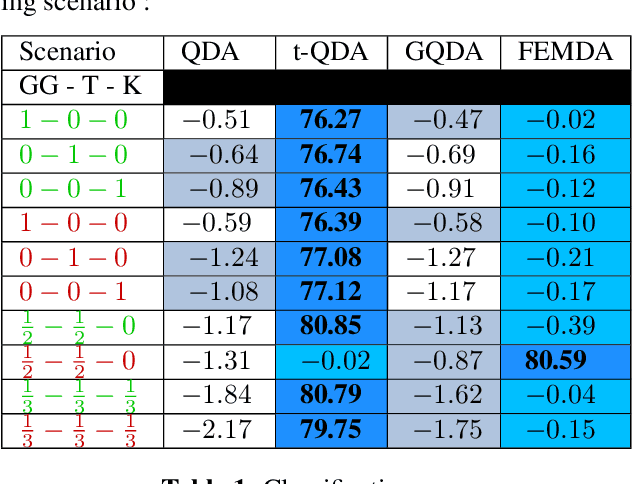
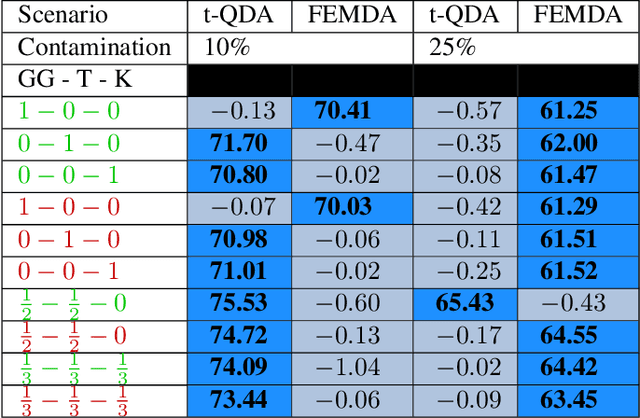
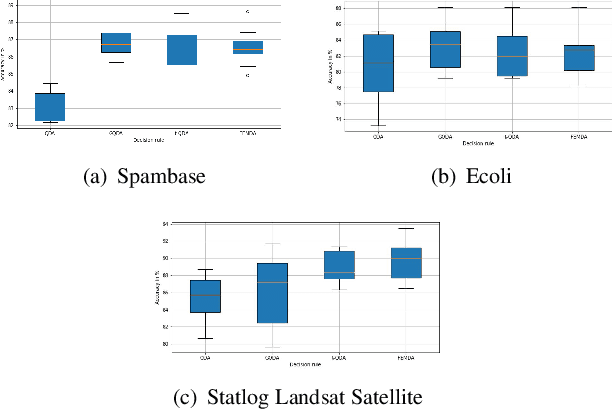
Linear and Quadratic Discriminant Analysis are well-known classical methods but can heavily suffer from non-Gaussian distributions and/or contaminated datasets, mainly because of the underlying Gaussian assumption that is not robust. To fill this gap, this paper presents a new robust discriminant analysis where each data point is drawn by its own arbitrary Elliptically Symmetrical (ES) distribution and its own arbitrary scale parameter. Such a model allows for possibly very heterogeneous, independent but non-identically distributed samples. After deriving a new decision rule, it is shown that maximum-likelihood parameter estimation and classification are very simple, fast and robust compared to state-of-the-art methods.

PCA-based Multi Task Learning: a Random Matrix Approach

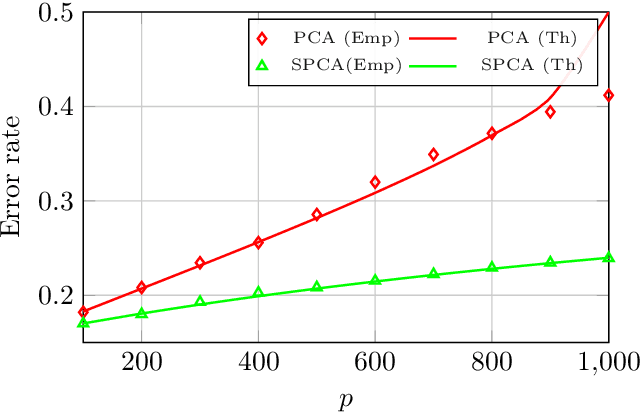
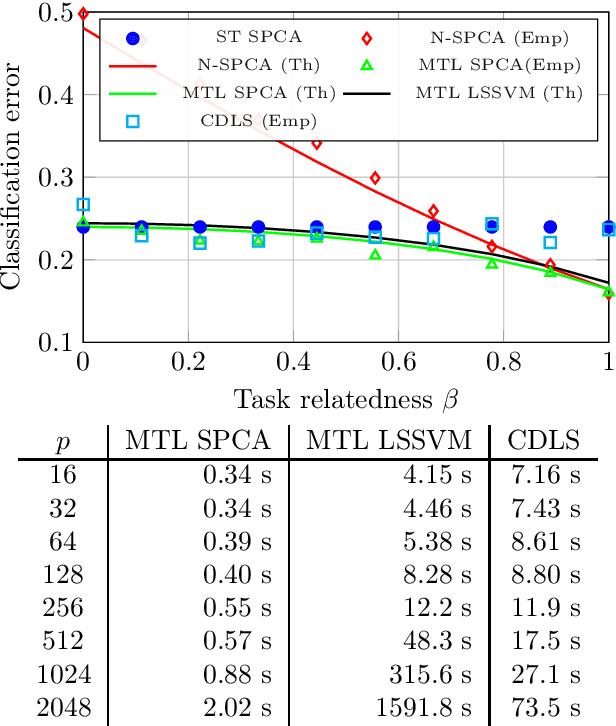
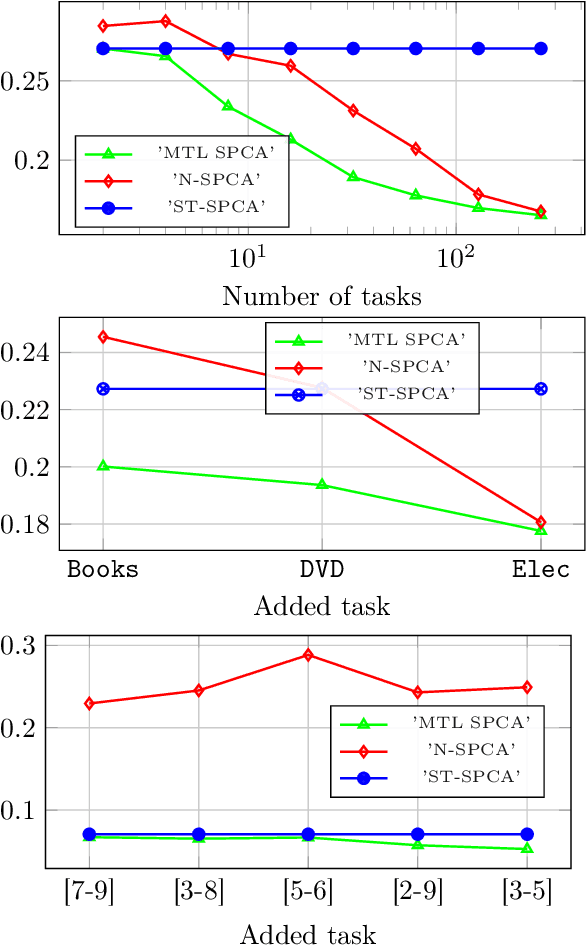
The article proposes and theoretically analyses a \emph{computationally efficient} multi-task learning (MTL) extension of popular principal component analysis (PCA)-based supervised learning schemes \cite{barshan2011supervised,bair2006prediction}. The analysis reveals that (i) by default learning may dramatically fail by suffering from \emph{negative transfer}, but that (ii) simple counter-measures on data labels avert negative transfer and necessarily result in improved performances. Supporting experiments on synthetic and real data benchmarks show that the proposed method achieves comparable performance with state-of-the-art MTL methods but at a \emph{significantly reduced computational cost}.

Riemannian classification of EEG signals with missing values

This paper proposes two strategies to handle missing data for the classification of electroencephalograms using covariance matrices. The first approach estimates the covariance from imputed data with the $k$-nearest neighbors algorithm; the second relies on the observed data by leveraging the observed-data likelihood within an expectation-maximization algorithm. Both approaches are combined with the minimum distance to Riemannian mean classifier and applied to a classification task of event related-potentials, a widely known paradigm of brain-computer interface paradigms. As results show, the proposed strategies perform better than the classification based on observed data and allow to keep a high accuracy even when the missing data ratio increases.

Joint Estimation of Location and Scatter in Complex Elliptical Distributions: A robust semiparametric and computationally efficient $R$-estimator of the shape matrix

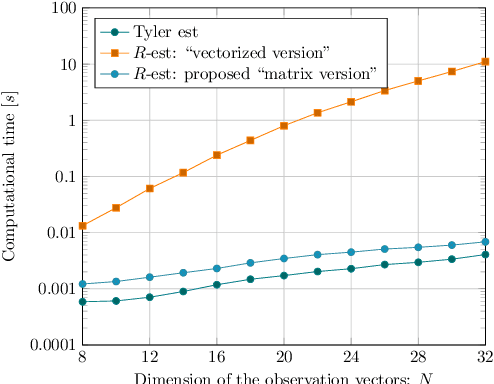
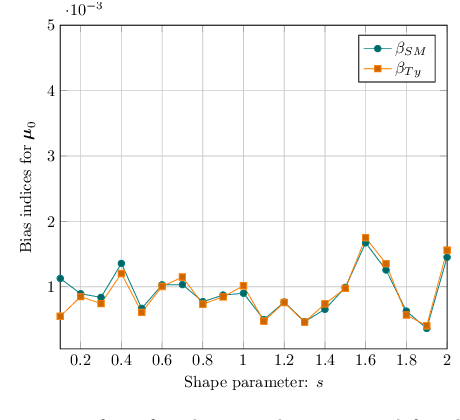
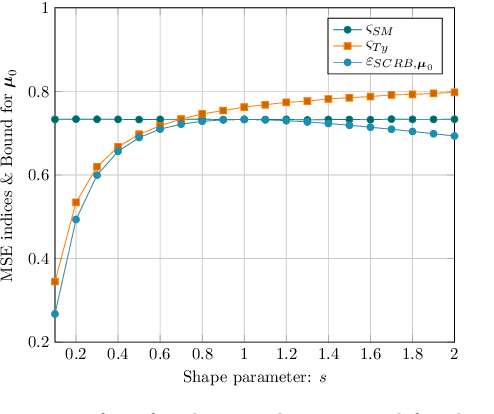
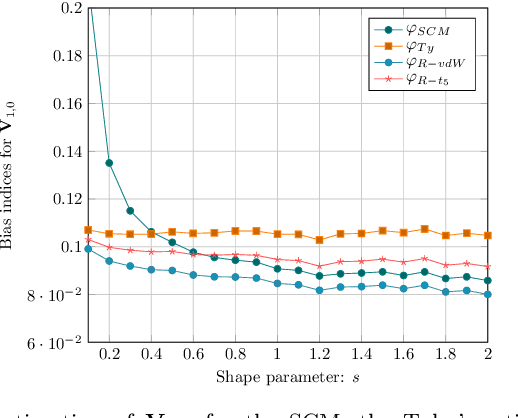
The joint estimation of the location vector and the shape matrix of a set of independent and identically Complex Elliptically Symmetric (CES) distributed observations is investigated from both the theoretical and computational viewpoints. This joint estimation problem is framed in the original context of semiparametric models allowing us to handle the (generally unknown) density generator as an \textit{infinite-dimensional} nuisance parameter. In the first part of the paper, a computationally efficient and memory saving implementation of the robust and semiparmaetric efficient $R$-estimator for shape matrices is derived. Building upon this result, in the second part, a joint estimator, relying on the Tyler's $M$-estimator of location and on the $R$-estimator of shape matrix, is proposed and its Mean Squared Error (MSE) performance compared with the Semiparametric Cram\'{e}r-Rao Bound (CSCRB).