A Robust and Flexible EM Algorithm for Mixtures of Elliptical Distributions with Missing Data

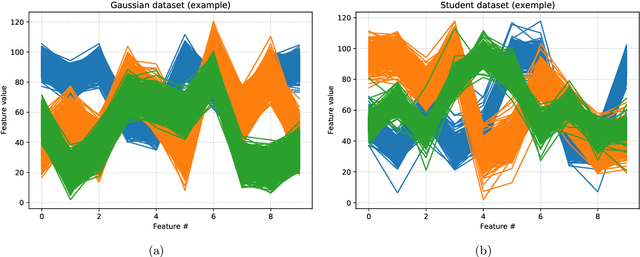
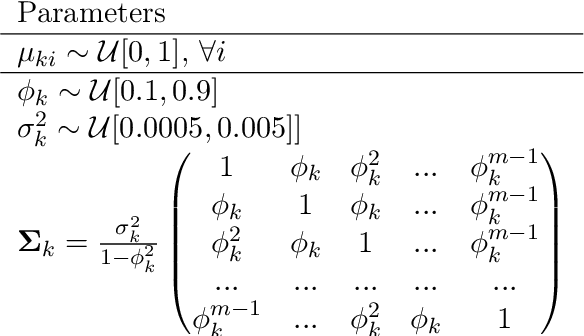
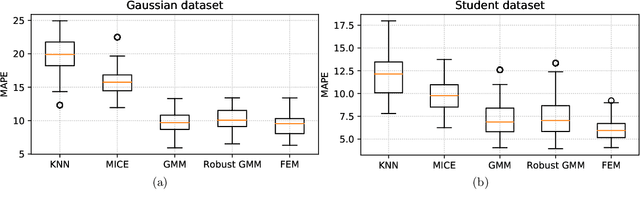
This paper tackles the problem of missing data imputation for noisy and non-Gaussian data. A classical imputation method, the Expectation Maximization (EM) algorithm for Gaussian mixture models, has shown interesting properties when compared to other popular approaches such as those based on k-nearest neighbors or on multiple imputations by chained equations. However, Gaussian mixture models are known to be not robust to heterogeneous data, which can lead to poor estimation performance when the data is contaminated by outliers or come from a non-Gaussian distributions. To overcome this issue, a new expectation maximization algorithm is investigated for mixtures of elliptical distributions with the nice property of handling potential missing data. The complete-data likelihood associated with mixtures of elliptical distributions is well adapted to the EM framework thanks to its conditional distribution, which is shown to be a Student distribution. Experimental results on synthetic data demonstrate that the proposed algorithm is robust to outliers and can be used with non-Gaussian data. Furthermore, experiments conducted on real-world datasets show that this algorithm is very competitive when compared to other classical imputation methods.

Riemannian classification of EEG signals with missing values

This paper proposes two strategies to handle missing data for the classification of electroencephalograms using covariance matrices. The first approach estimates the covariance from imputed data with the $k$-nearest neighbors algorithm; the second relies on the observed data by leveraging the observed-data likelihood within an expectation-maximization algorithm. Both approaches are combined with the minimum distance to Riemannian mean classifier and applied to a classification task of event related-potentials, a widely known paradigm of brain-computer interface paradigms. As results show, the proposed strategies perform better than the classification based on observed data and allow to keep a high accuracy even when the missing data ratio increases.

Robust low-rank covariance matrix estimation with a general pattern of missing values

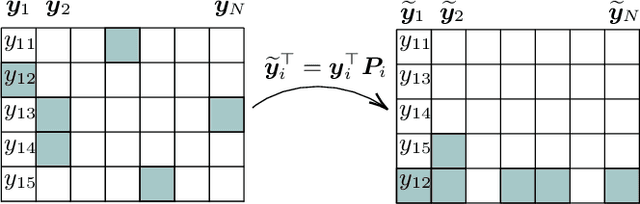
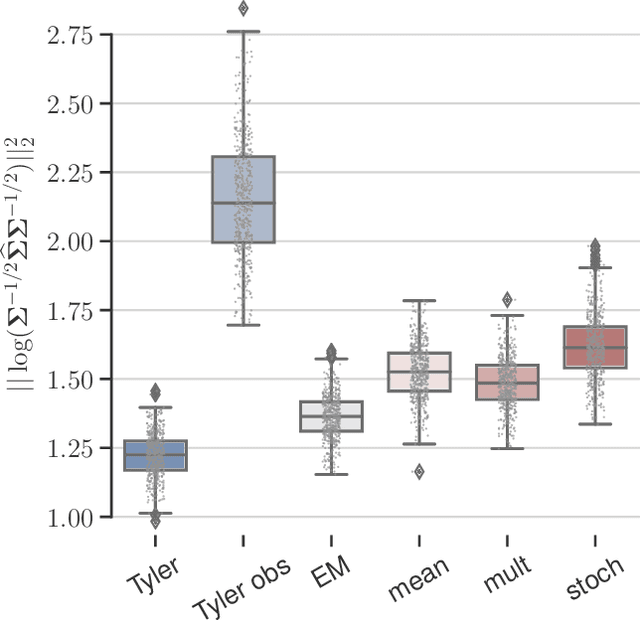
This paper tackles the problem of robust covariance matrix estimation when the data is incomplete. Classical statistical estimation methodologies are usually built upon the Gaussian assumption, whereas existing robust estimation ones assume unstructured signal models. The former can be inaccurate in real-world data sets in which heterogeneity causes heavy-tail distributions, while the latter does not profit from the usual low-rank structure of the signal. Taking advantage of both worlds, a covariance matrix estimation procedure is designed on a robust (compound Gaussian) low-rank model by leveraging the observed-data likelihood function within an expectation-maximization algorithm. It is also designed to handle general pattern of missing values. The proposed procedure is first validated on simulated data sets. Then, its interest for classification and clustering applications is assessed on two real data sets with missing values, which include multispectral and hyperspectral time series.