A Robust and Flexible EM Algorithm for Mixtures of Elliptical Distributions with Missing Data
Paper and Code
Jan 28, 2022
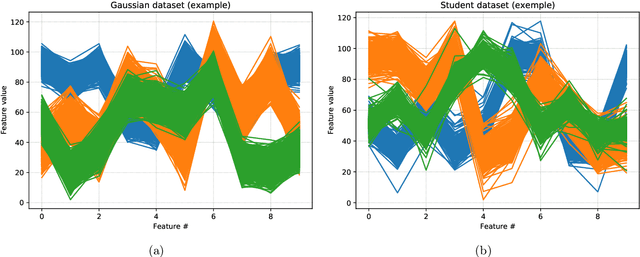
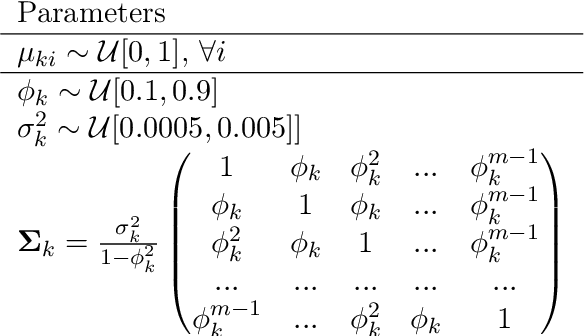
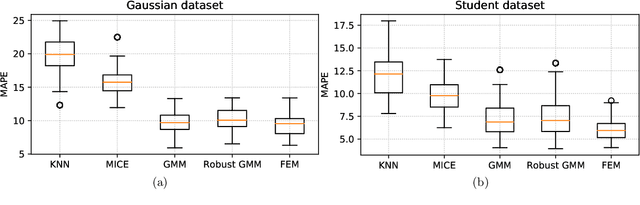
This paper tackles the problem of missing data imputation for noisy and non-Gaussian data. A classical imputation method, the Expectation Maximization (EM) algorithm for Gaussian mixture models, has shown interesting properties when compared to other popular approaches such as those based on k-nearest neighbors or on multiple imputations by chained equations. However, Gaussian mixture models are known to be not robust to heterogeneous data, which can lead to poor estimation performance when the data is contaminated by outliers or come from a non-Gaussian distributions. To overcome this issue, a new expectation maximization algorithm is investigated for mixtures of elliptical distributions with the nice property of handling potential missing data. The complete-data likelihood associated with mixtures of elliptical distributions is well adapted to the EM framework thanks to its conditional distribution, which is shown to be a Student distribution. Experimental results on synthetic data demonstrate that the proposed algorithm is robust to outliers and can be used with non-Gaussian data. Furthermore, experiments conducted on real-world datasets show that this algorithm is very competitive when compared to other classical imputation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge