Elliptical Wishart distributions: information geometry, maximum likelihood estimator, performance analysis and statistical learning

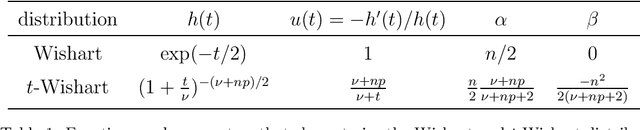
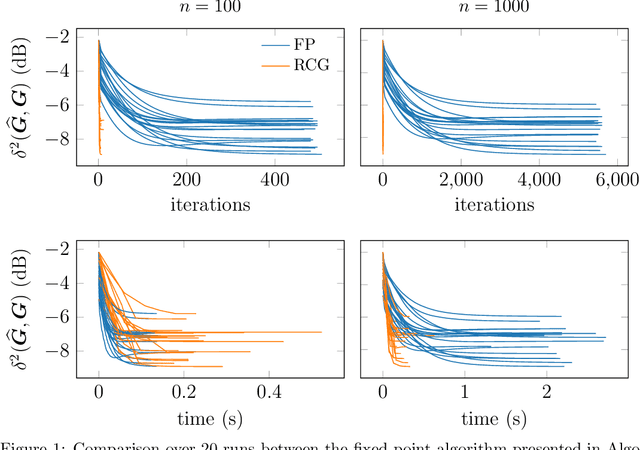
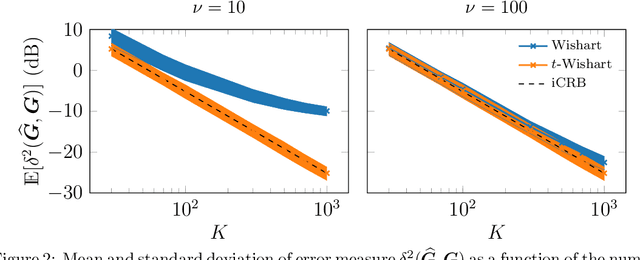
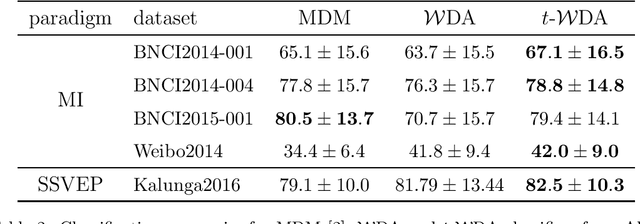
This paper deals with Elliptical Wishart distributions - which generalize the Wishart distribution - in the context of signal processing and machine learning. Two algorithms to compute the maximum likelihood estimator (MLE) are proposed: a fixed point algorithm and a Riemannian optimization method based on the derived information geometry of Elliptical Wishart distributions. The existence and uniqueness of the MLE are characterized as well as the convergence of both estimation algorithms. Statistical properties of the MLE are also investigated such as consistency, asymptotic normality and an intrinsic version of Fisher efficiency. On the statistical learning side, novel classification and clustering methods are designed. For the $t$-Wishart distribution, the performance of the MLE and statistical learning algorithms are evaluated on both simulated and real EEG and hyperspectral data, showcasing the interest of our proposed methods.

Random matrix theory improved Fréchet mean of symmetric positive definite matrices

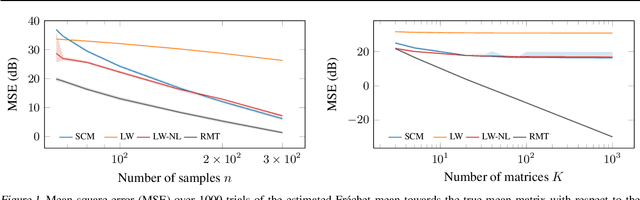
In this study, we consider the realm of covariance matrices in machine learning, particularly focusing on computing Fr\'echet means on the manifold of symmetric positive definite matrices, commonly referred to as Karcher or geometric means. Such means are leveraged in numerous machine-learning tasks. Relying on advanced statistical tools, we introduce a random matrix theory-based method that estimates Fr\'echet means, which is particularly beneficial when dealing with low sample support and a high number of matrices to average. Our experimental evaluation, involving both synthetic and real-world EEG and hyperspectral datasets, shows that we largely outperform state-of-the-art methods.

Natural Bayesian Cramér-Rao Bound with an Application to Covariance Estimation

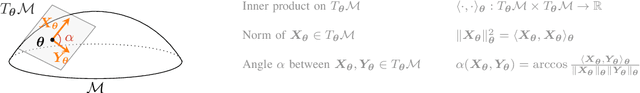
In this paper, we propose to develop a new Cram\'er-Rao Bound (CRB) when the parameter to estimate lies in a manifold and follows a prior distribution. This derivation leads to a natural inequality between an error criteria based on geometrical properties and this new bound. This main contribution is illustrated in the problem of covariance estimation when the data follow a Gaussian distribution and the prior distribution is an inverse Wishart. Numerical simulation shows new results where the proposed CRB allows to exhibit interesting properties of the MAP estimator which are not observed with the classical Bayesian CRB.

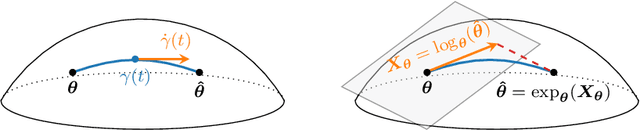
The Fisher-Rao geometry of CES distributions

When dealing with a parametric statistical model, a Riemannian manifold can naturally appear by endowing the parameter space with the Fisher information metric. The geometry induced on the parameters by this metric is then referred to as the Fisher-Rao information geometry. Interestingly, this yields a point of view that allows for leveragingmany tools from differential geometry. After a brief introduction about these concepts, we will present some practical uses of these geometric tools in the framework of elliptical distributions. This second part of the exposition is divided into three main axes: Riemannian optimization for covariance matrix estimation, Intrinsic Cram\'er-Rao bounds, and classification using Riemannian distances.

Riemannian classification of EEG signals with missing values

This paper proposes two strategies to handle missing data for the classification of electroencephalograms using covariance matrices. The first approach estimates the covariance from imputed data with the $k$-nearest neighbors algorithm; the second relies on the observed data by leveraging the observed-data likelihood within an expectation-maximization algorithm. Both approaches are combined with the minimum distance to Riemannian mean classifier and applied to a classification task of event related-potentials, a widely known paradigm of brain-computer interface paradigms. As results show, the proposed strategies perform better than the classification based on observed data and allow to keep a high accuracy even when the missing data ratio increases.

Riemannian geometry for Compound Gaussian distributions: application to recursive change detection

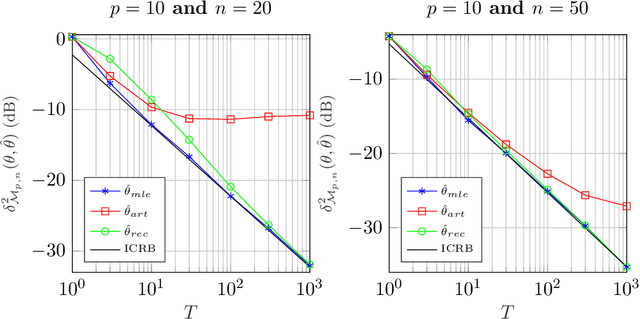
A new Riemannian geometry for the Compound Gaussian distribution is proposed. In particular, the Fisher information metric is obtained, along with corresponding geodesics and distance function. This new geometry is applied on a change detection problem on Multivariate Image Times Series: a recursive approach based on Riemannian optimization is developed. As shown on simulated data, it allows to reach optimal performance while being computationally more efficient.

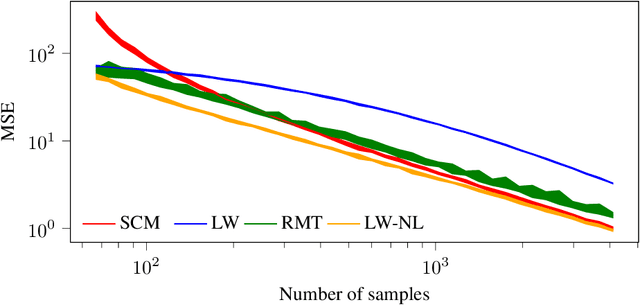
Random Matrix Improved Covariance Estimation for a Large Class of Metrics

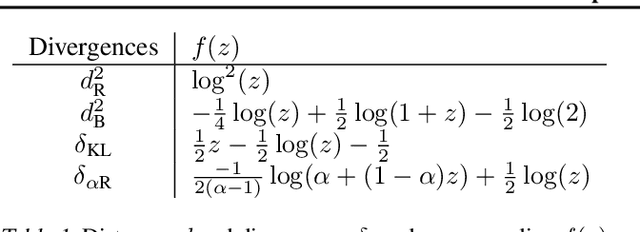
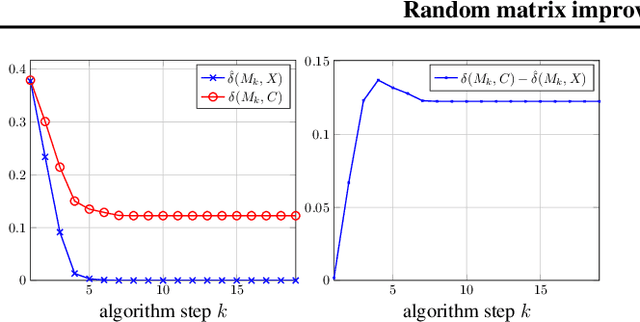
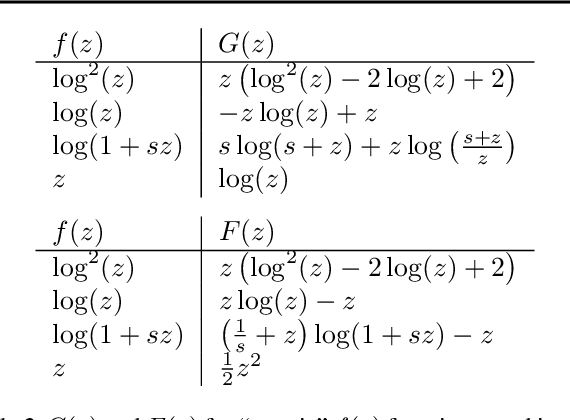
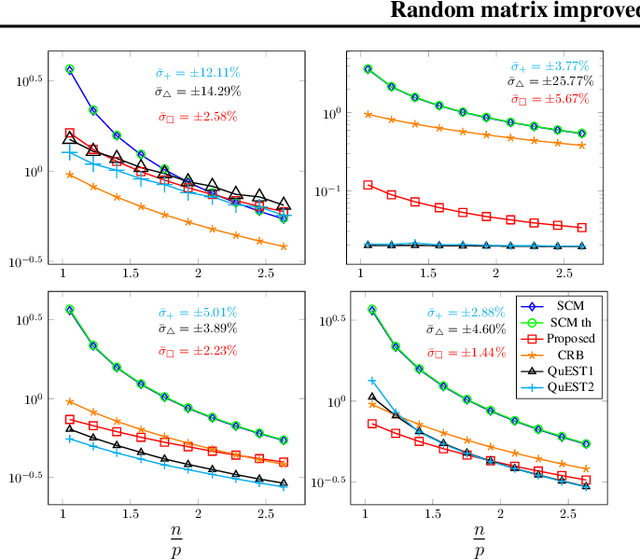
Relying on recent advances in statistical estimation of covariance distances based on random matrix theory, this article proposes an improved covariance and precision matrix estimation for a wide family of metrics. The method is shown to largely outperform the sample covariance matrix estimate and to compete with state-of-the-art methods, while at the same time being computationally simpler. Applications to linear and quadratic discriminant analyses also demonstrate significant gains, therefore suggesting practical interest to statistical machine learning.