POMDP-Driven Cognitive Massive MIMO Radar: Joint Target Detection-Tracking In Unknown Disturbances

The joint detection and tracking of a moving target embedded in an unknown disturbance represents a key feature that motivates the development of the cognitive radar paradigm. Building upon recent advancements in robust target detection with multiple-input multiple-output (MIMO) radars, this work explores the application of a Partially Observable Markov Decision Process (POMDP) framework to enhance the tracking and detection tasks in a statistically unknown environment. In the POMDP setup, the radar system is considered as an intelligent agent that continuously senses the surrounding environment, optimizing its actions to maximize the probability of detection $(P_D)$ and improve the target position and velocity estimation, all this while keeping a constant probability of false alarm $(P_{FA})$. The proposed approach employs an online algorithm that does not require any apriori knowledge of the noise statistics, and it relies on a much more general observation model than the traditional range-azimuth-elevation model employed by conventional tracking algorithms. Simulation results clearly show substantial performance improvement of the POMDP-based algorithm compared to the State-Action-Reward-State-Action (SARSA)-based one that has been recently investigated in the context of massive MIMO (MMIMO) radar systems.

Natural Bayesian Cramér-Rao Bound with an Application to Covariance Estimation

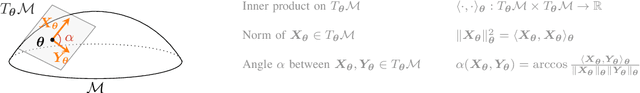
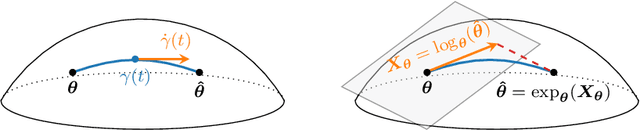
In this paper, we propose to develop a new Cram\'er-Rao Bound (CRB) when the parameter to estimate lies in a manifold and follows a prior distribution. This derivation leads to a natural inequality between an error criteria based on geometrical properties and this new bound. This main contribution is illustrated in the problem of covariance estimation when the data follow a Gaussian distribution and the prior distribution is an inverse Wishart. Numerical simulation shows new results where the proposed CRB allows to exhibit interesting properties of the MAP estimator which are not observed with the classical Bayesian CRB.

The Fisher-Rao geometry of CES distributions

When dealing with a parametric statistical model, a Riemannian manifold can naturally appear by endowing the parameter space with the Fisher information metric. The geometry induced on the parameters by this metric is then referred to as the Fisher-Rao information geometry. Interestingly, this yields a point of view that allows for leveragingmany tools from differential geometry. After a brief introduction about these concepts, we will present some practical uses of these geometric tools in the framework of elliptical distributions. This second part of the exposition is divided into three main axes: Riemannian optimization for covariance matrix estimation, Intrinsic Cram\'er-Rao bounds, and classification using Riemannian distances.

Joint Estimation of Location and Scatter in Complex Elliptical Distributions: A robust semiparametric and computationally efficient $R$-estimator of the shape matrix

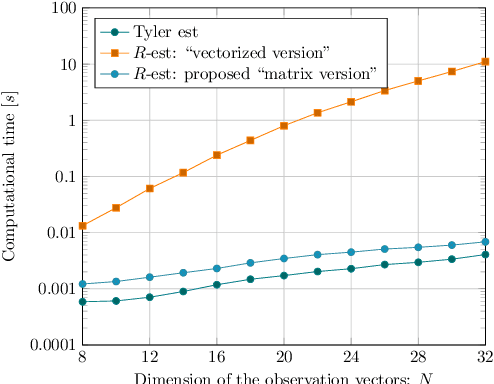
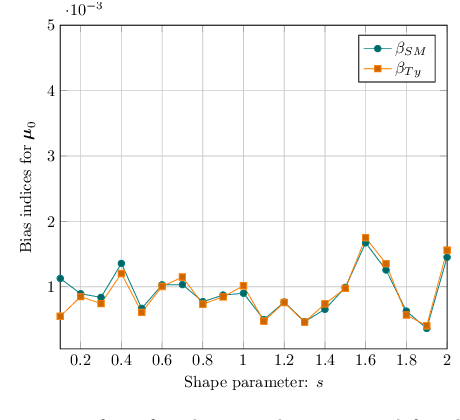
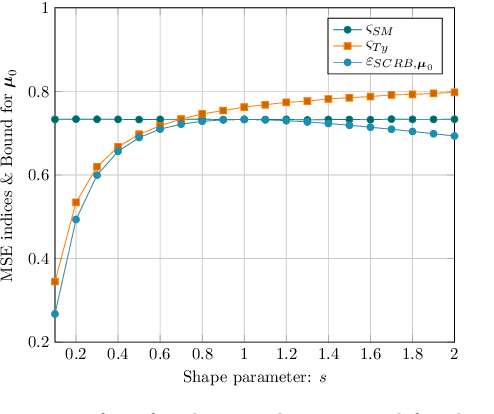
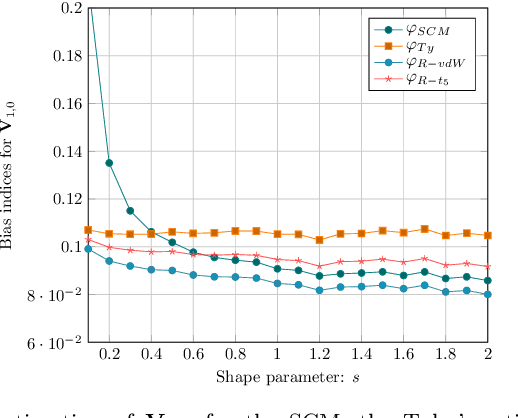
The joint estimation of the location vector and the shape matrix of a set of independent and identically Complex Elliptically Symmetric (CES) distributed observations is investigated from both the theoretical and computational viewpoints. This joint estimation problem is framed in the original context of semiparametric models allowing us to handle the (generally unknown) density generator as an \textit{infinite-dimensional} nuisance parameter. In the first part of the paper, a computationally efficient and memory saving implementation of the robust and semiparmaetric efficient $R$-estimator for shape matrices is derived. Building upon this result, in the second part, a joint estimator, relying on the Tyler's $M$-estimator of location and on the $R$-estimator of shape matrix, is proposed and its Mean Squared Error (MSE) performance compared with the Semiparametric Cram\'{e}r-Rao Bound (CSCRB).