Sparse PCA with False Discovery Rate Controlled Variable Selection

Sparse principal component analysis (PCA) aims at mapping large dimensional data to a linear subspace of lower dimension. By imposing loading vectors to be sparse, it performs the double duty of dimension reduction and variable selection. Sparse PCA algorithms are usually expressed as a trade-off between explained variance and sparsity of the loading vectors (i.e., number of selected variables). As a high explained variance is not necessarily synonymous with relevant information, these methods are prone to select irrelevant variables. To overcome this issue, we propose an alternative formulation of sparse PCA driven by the false discovery rate (FDR). We then leverage the Terminating-Random Experiments (T-Rex) selector to automatically determine an FDR-controlled support of the loading vectors. A major advantage of the resulting T-Rex PCA is that no sparsity parameter tuning is required. Numerical experiments and a stock market data example demonstrate a significant performance improvement.

Natural Bayesian Cramér-Rao Bound with an Application to Covariance Estimation

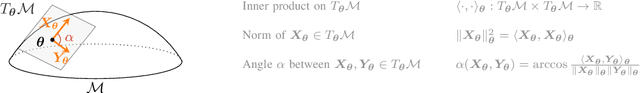
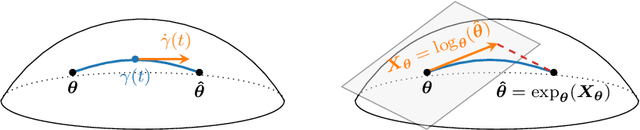
In this paper, we propose to develop a new Cram\'er-Rao Bound (CRB) when the parameter to estimate lies in a manifold and follows a prior distribution. This derivation leads to a natural inequality between an error criteria based on geometrical properties and this new bound. This main contribution is illustrated in the problem of covariance estimation when the data follow a Gaussian distribution and the prior distribution is an inverse Wishart. Numerical simulation shows new results where the proposed CRB allows to exhibit interesting properties of the MAP estimator which are not observed with the classical Bayesian CRB.

The Fisher-Rao geometry of CES distributions

When dealing with a parametric statistical model, a Riemannian manifold can naturally appear by endowing the parameter space with the Fisher information metric. The geometry induced on the parameters by this metric is then referred to as the Fisher-Rao information geometry. Interestingly, this yields a point of view that allows for leveragingmany tools from differential geometry. After a brief introduction about these concepts, we will present some practical uses of these geometric tools in the framework of elliptical distributions. This second part of the exposition is divided into three main axes: Riemannian optimization for covariance matrix estimation, Intrinsic Cram\'er-Rao bounds, and classification using Riemannian distances.

Entropic Wasserstein Component Analysis

Dimension reduction (DR) methods provide systematic approaches for analyzing high-dimensional data. A key requirement for DR is to incorporate global dependencies among original and embedded samples while preserving clusters in the embedding space. To achieve this, we combine the principles of optimal transport (OT) and principal component analysis (PCA). Our method seeks the best linear subspace that minimizes reconstruction error using entropic OT, which naturally encodes the neighborhood information of the samples. From an algorithmic standpoint, we propose an efficient block-majorization-minimization solver over the Stiefel manifold. Our experimental results demonstrate that our approach can effectively preserve high-dimensional clusters, leading to more interpretable and effective embeddings. Python code of the algorithms and experiments is available online.

Riemannian optimization for non-centered mixture of scaled Gaussian distributions

This paper studies the statistical model of the non-centered mixture of scaled Gaussian distributions (NC-MSG). Using the Fisher-Rao information geometry associated to this distribution, we derive a Riemannian gradient descent algorithm. This algorithm is leveraged for two minimization problems. The first one is the minimization of a regularized negative log- likelihood (NLL). The latter makes the trade-off between a white Gaussian distribution and the NC-MSG. Conditions on the regularization are given so that the existence of a minimum to this problem is guaranteed without assumptions on the samples. Then, the Kullback-Leibler (KL) divergence between two NC-MSG is derived. This divergence enables us to define a minimization problem to compute centers of mass of several NC-MSGs. The proposed Riemannian gradient descent algorithm is leveraged to solve this second minimization problem. Numerical experiments show the good performance and the speed of the Riemannian gradient descent on the two problems. Finally, a Nearest centroid classifier is implemented leveraging the KL divergence and its associated center of mass. Applied on the large scale dataset Breizhcrops, this classifier shows good accuracies as well as robustness to rigid transformations of the test set.

Robust Geometric Metric Learning

This paper proposes new algorithms for the metric learning problem. We start by noticing that several classical metric learning formulations from the literature can be viewed as modified covariance matrix estimation problems. Leveraging this point of view, a general approach, called Robust Geometric Metric Learning (RGML), is then studied. This method aims at simultaneously estimating the covariance matrix of each class while shrinking them towards their (unknown) barycenter. We focus on two specific costs functions: one associated with the Gaussian likelihood (RGML Gaussian), and one with Tyler's M -estimator (RGML Tyler). In both, the barycenter is defined with the Riemannian distance, which enjoys nice properties of geodesic convexity and affine invariance. The optimization is performed using the Riemannian geometry of symmetric positive definite matrices and its submanifold of unit determinant. Finally, the performance of RGML is asserted on real datasets. Strong performance is exhibited while being robust to mislabeled data.

Multifrequency Array Calibration in Presence of Radio Frequency Interferences

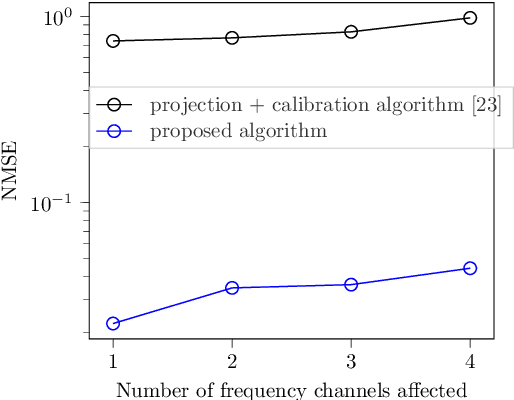
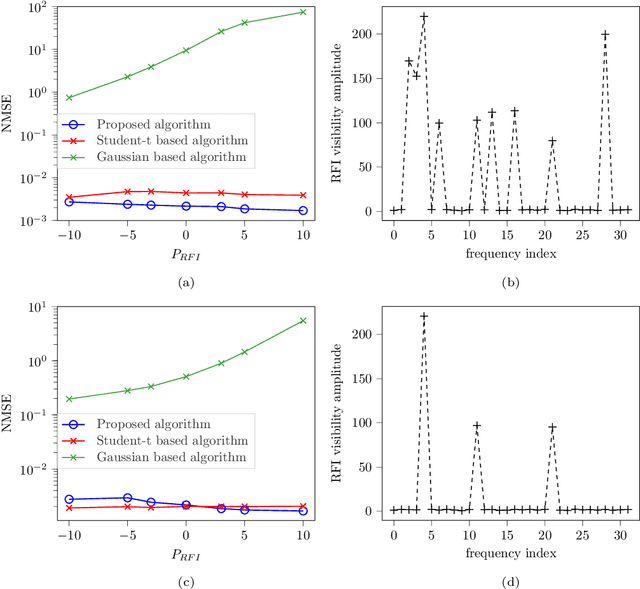
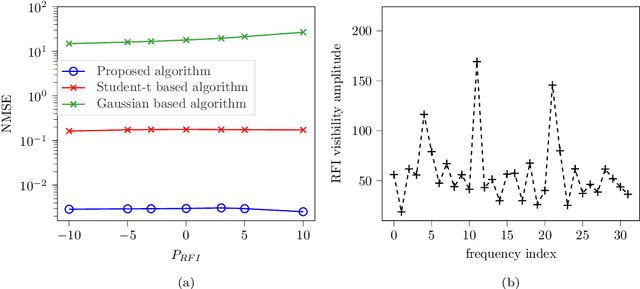
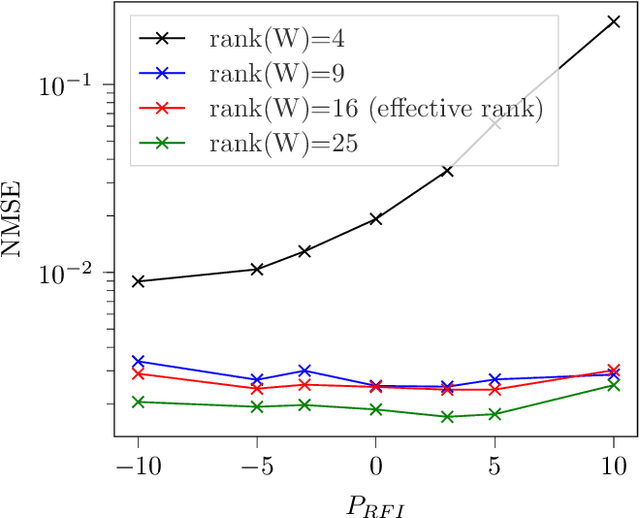
Radio interferometers are phased arrays producing high-resolution images from the covariance matrix of measurements. Calibration of such instruments is necessary and is a critical task. This is how the estimation of instrumental errors is usually done thanks to the knowledge of referenced celestial sources. However, the use of high sensitive antennas in modern radio interferometers (LOFAR, SKA) brings a new challenge in radio astronomy because there are more sensitive to Radio Frequency Interferences (RFI). The presence of RFI during the calibration process generally induces biases in state-of-the-art solutions. The purpose of this paper is to propose an alternative to alleviate the effects of RFI. For that, we first propose a model to take into account the presence of RFI in the data across multiple frequency channels thanks to a low-rank structured noise. We then achieve maximum likelihood estimation of the calibration parameters with a Space Alternating Generalized Expectation-Maximization (SAGE) algorithm for which we derive originally two sets of complete data allowing close form expressions for the updates. Numerical simulations show a significant gain in performance for RFI corrupted data in comparison with some more classical methods.

Robust low-rank covariance matrix estimation with a general pattern of missing values

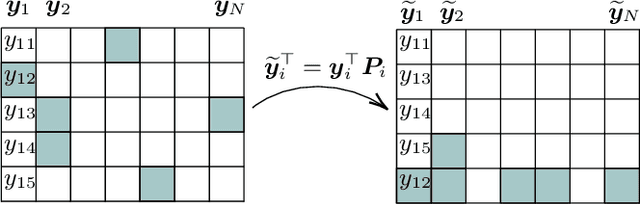
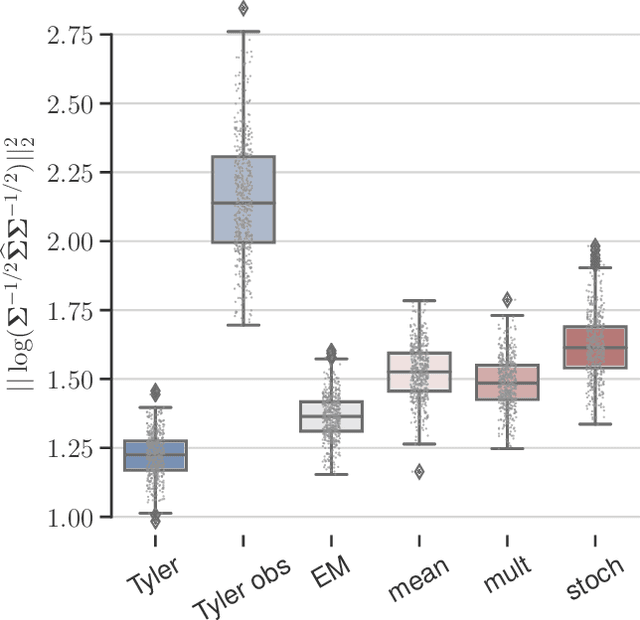
This paper tackles the problem of robust covariance matrix estimation when the data is incomplete. Classical statistical estimation methodologies are usually built upon the Gaussian assumption, whereas existing robust estimation ones assume unstructured signal models. The former can be inaccurate in real-world data sets in which heterogeneity causes heavy-tail distributions, while the latter does not profit from the usual low-rank structure of the signal. Taking advantage of both worlds, a covariance matrix estimation procedure is designed on a robust (compound Gaussian) low-rank model by leveraging the observed-data likelihood function within an expectation-maximization algorithm. It is also designed to handle general pattern of missing values. The proposed procedure is first validated on simulated data sets. Then, its interest for classification and clustering applications is assessed on two real data sets with missing values, which include multispectral and hyperspectral time series.