The Informed Elastic Net for Fast Grouped Variable Selection and FDR Control in Genomics Research

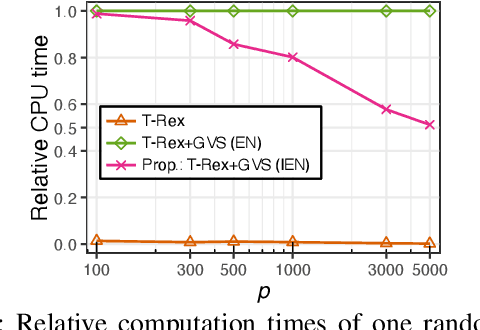
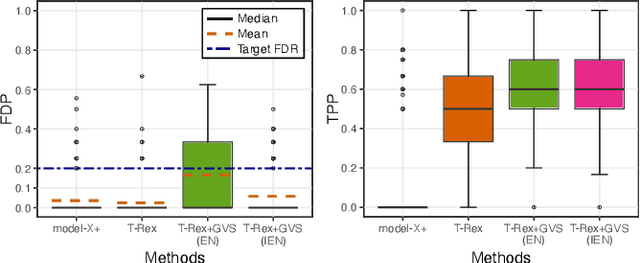
Modern genomics research relies on genome-wide association studies (GWAS) to identify the few genetic variants among potentially millions that are associated with diseases of interest. Only reproducible discoveries of groups of associations improve our understanding of complex polygenic diseases and enable the development of new drugs and personalized medicine. Thus, fast multivariate variable selection methods that have a high true positive rate (TPR) while controlling the false discovery rate (FDR) are crucial. Recently, the T-Rex+GVS selector, a version of the T-Rex selector that uses the elastic net (EN) as a base selector to perform grouped variable election, was proposed. Although it significantly increased the TPR in simulated GWAS compared to the original T-Rex, its comparably high computational cost limits scalability. Therefore, we propose the informed elastic net (IEN), a new base selector that significantly reduces computation time while retaining the grouped variable selection property. We quantify its grouping effect and derive its formulation as a Lasso-type optimization problem, which is solved efficiently within the T-Rex framework by the terminated LARS algorithm. Numerical simulations and a GWAS study demonstrate that the proposed T-Rex+GVS (IEN) exhibits the desired grouping effect, reduces computation time, and achieves the same TPR as T-Rex+GVS (EN) but with lower FDR, which makes it a promising method for large-scale GWAS.

Solving FDR-Controlled Sparse Regression Problems with Five Million Variables on a Laptop

Currently, there is an urgent demand for scalable multivariate and high-dimensional false discovery rate (FDR)-controlling variable selection methods to ensure the repro-ducibility of discoveries. However, among existing methods, only the recently proposed Terminating-Random Experiments (T-Rex) selector scales to problems with millions of variables, as encountered in, e.g., genomics research. The T-Rex selector is a new learning framework based on early terminated random experiments with computer-generated dummy variables. In this work, we propose the Big T-Rex, a new implementation of T-Rex that drastically reduces its Random Access Memory (RAM) consumption to enable solving FDR-controlled sparse regression problems with millions of variables on a laptop. We incorporate advanced memory-mapping techniques to work with matrices that reside on solid-state drive and two new dummy generation strategies based on permutations of a reference matrix. Our nu-merical experiments demonstrate a drastic reduction in memory demand and computation time. We showcase that the Big T-Rex can efficiently solve FDR-controlled Lasso-type problems with five million variables on a laptop in thirty minutes. Our work empowers researchers without access to high-performance clusters to make reproducible discoveries in large-scale high-dimensional data.

FDR-Controlled Portfolio Optimization for Sparse Financial Index Tracking

In high-dimensional data analysis, such as financial index tracking or biomedical applications, it is crucial to select the few relevant variables while maintaining control over the false discovery rate (FDR). In these applications, strong dependencies often exist among the variables (e.g., stock returns), which can undermine the FDR control property of existing methods like the model-X knockoff method or the T-Rex selector. To address this issue, we have expanded the T-Rex framework to accommodate overlapping groups of highly correlated variables. This is achieved by integrating a nearest neighbors penalization mechanism into the framework, which provably controls the FDR at the user-defined target level. A real-world example of sparse index tracking demonstrates the proposed method's ability to accurately track the S&P 500 index over the past 20 years based on a small number of stocks. An open-source implementation is provided within the R package TRexSelector on CRAN.

High-Dimensional False Discovery Rate Control for Dependent Variables

Algorithms that ensure reproducible findings from large-scale, high-dimensional data are pivotal in numerous signal processing applications. In recent years, multivariate false discovery rate (FDR) controlling methods have emerged, providing guarantees even in high-dimensional settings where the number of variables surpasses the number of samples. However, these methods often fail to reliably control the FDR in the presence of highly dependent variable groups, a common characteristic in fields such as genomics and finance. To tackle this critical issue, we introduce a novel framework that accounts for general dependency structures. Our proposed dependency-aware T-Rex selector integrates hierarchical graphical models within the T-Rex framework to effectively harness the dependency structure among variables. Leveraging martingale theory, we prove that our variable penalization mechanism ensures FDR control. We further generalize the FDR-controlling framework by stating and proving a clear condition necessary for designing both graphical and non-graphical models that capture dependencies. Additionally, we formulate a fully integrated optimal calibration algorithm that concurrently determines the parameters of the graphical model and the T-Rex framework, such that the FDR is controlled while maximizing the number of selected variables. Numerical experiments and a breast cancer survival analysis use-case demonstrate that the proposed method is the only one among the state-of-the-art benchmark methods that controls the FDR and reliably detects genes that have been previously identified to be related to breast cancer. An open-source implementation is available within the R package TRexSelector on CRAN.

False Discovery Rate Control for Gaussian Graphical Models via Neighborhood Screening

Gaussian graphical models emerge in a wide range of fields. They model the statistical relationships between variables as a graph, where an edge between two variables indicates conditional dependence. Unfortunately, well-established estimators, such as the graphical lasso or neighborhood selection, are known to be susceptible to a high prevalence of false edge detections. False detections may encourage inaccurate or even incorrect scientific interpretations, with major implications in applications, such as biomedicine or healthcare. In this paper, we introduce a nodewise variable selection approach to graph learning and provably control the false discovery rate of the selected edge set at a self-estimated level. A novel fusion method of the individual neighborhoods outputs an undirected graph estimate. The proposed method is parameter-free and does not require tuning by the user. Benchmarks against competing false discovery rate controlling methods in numerical experiments considering different graph topologies show a significant gain in performance.

Sparse PCA with False Discovery Rate Controlled Variable Selection

Sparse principal component analysis (PCA) aims at mapping large dimensional data to a linear subspace of lower dimension. By imposing loading vectors to be sparse, it performs the double duty of dimension reduction and variable selection. Sparse PCA algorithms are usually expressed as a trade-off between explained variance and sparsity of the loading vectors (i.e., number of selected variables). As a high explained variance is not necessarily synonymous with relevant information, these methods are prone to select irrelevant variables. To overcome this issue, we propose an alternative formulation of sparse PCA driven by the false discovery rate (FDR). We then leverage the Terminating-Random Experiments (T-Rex) selector to automatically determine an FDR-controlled support of the loading vectors. A major advantage of the resulting T-Rex PCA is that no sparsity parameter tuning is required. Numerical experiments and a stock market data example demonstrate a significant performance improvement.

The Terminating-Knockoff Filter: Fast High-Dimensional Variable Selection with False Discovery Rate Control

We propose the Terminating-Knockoff (T-Knock) filter, a fast variable selection method for high-dimensional data. The T-Knock filter controls a user-defined target false discovery rate (FDR) while maximizing the number of selected true positives. This is achieved by fusing the solutions of multiple early terminated random experiments. The experiments are conducted on a combination of the original data and multiple sets of randomly generated knockoff variables. A finite sample proof based on martingale theory for the FDR control property is provided. Numerical simulations show that the FDR is controlled at the target level while allowing for a high power. We prove under mild conditions that the knockoffs can be sampled from any univariate distribution. The computational complexity of the proposed method is derived and it is demonstrated via numerical simulations that the sequential computation time is multiple orders of magnitude lower than that of the strongest benchmark methods in sparse high-dimensional settings. The T-Knock filter outperforms state-of-the-art methods for FDR control on a simulated genome-wide association study (GWAS), while its computation time is more than two orders of magnitude lower than that of the strongest benchmark methods.