Robust Filtering and Learning in State-Space Models: Skewness and Heavy Tails Via Asymmetric Laplace Distribution

State-space models are pivotal for dynamic system analysis but often struggle with outlier data that deviates from Gaussian distributions, frequently exhibiting skewness and heavy tails. This paper introduces a robust extension utilizing the asymmetric Laplace distribution, specifically tailored to capture these complex characteristics. We propose an efficient variational Bayes algorithm and a novel single-loop parameter estimation strategy, significantly enhancing the efficiency of the filtering, smoothing, and parameter estimation processes. Our comprehensive experiments demonstrate that our methods provide consistently robust performance across various noise settings without the need for manual hyperparameter adjustments. In stark contrast, existing models generally rely on specific noise conditions and necessitate extensive manual tuning. Moreover, our approach uses far fewer computational resources, thereby validating the model's effectiveness and underscoring its potential for practical applications in fields such as robust control and financial modeling.

Clustering of Incomplete Data via a Bipartite Graph Structure

There are various approaches to graph learning for data clustering, incorporating different spectral and structural constraints through diverse graph structures. Some methods rely on bipartite graph models, where nodes are divided into two classes: centers and members. These models typically require access to data for the center nodes in addition to observations from the member nodes. However, such additional data may not always be available in many practical scenarios. Moreover, popular Gaussian models for graph learning have demonstrated limited effectiveness in modeling data with heavy-tailed distributions, which are common in financial markets. In this paper, we propose a clustering method based on a bipartite graph model that addresses these challenges. First, it can infer clusters from incomplete data without requiring information about the center nodes. Second, it is designed to effectively handle heavy-tailed data. Numerical experiments using real financial data validate the efficiency of the proposed method for data clustering.

Time-Varying Graph Learning for Data with Heavy-Tailed Distribution

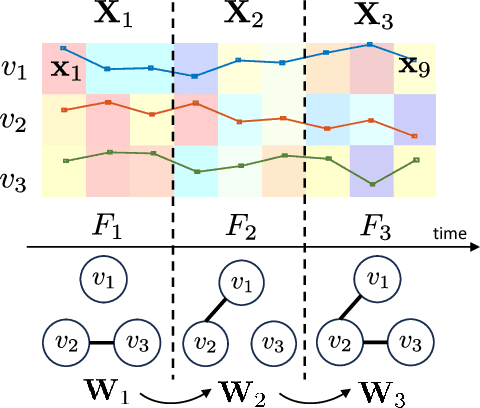
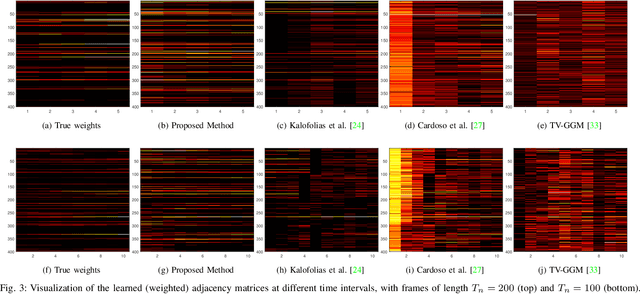
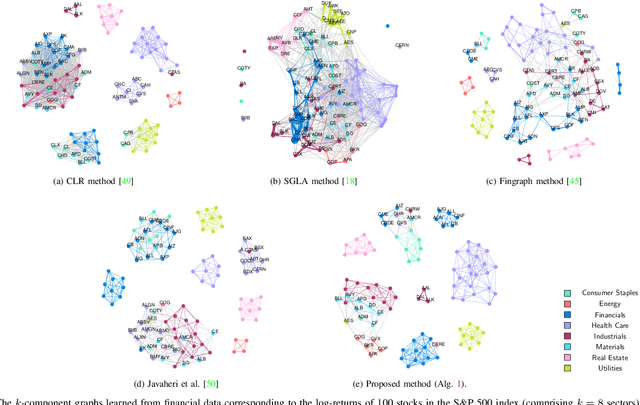
Graph models provide efficient tools to capture the underlying structure of data defined over networks. Many real-world network topologies are subject to change over time. Learning to model the dynamic interactions between entities in such networks is known as time-varying graph learning. Current methodology for learning such models often lacks robustness to outliers in the data and fails to handle heavy-tailed distributions, a common feature in many real-world datasets (e.g., financial data). This paper addresses the problem of learning time-varying graph models capable of efficiently representing heavy-tailed data. Unlike traditional approaches, we incorporate graph structures with specific spectral properties to enhance data clustering in our model. Our proposed method, which can also deal with noise and missing values in the data, is based on a stochastic approach, where a non-negative vector auto-regressive (VAR) model captures the variations in the graph and a Student-t distribution models the signal originating from this underlying time-varying graph. We propose an iterative method to learn time-varying graph topologies within a semi-online framework where only a mini-batch of data is used to update the graph. Simulations with both synthetic and real datasets demonstrate the efficacy of our model in analyzing heavy-tailed data, particularly those found in financial markets.

Robust and Constrained Estimation of State-Space Models: A Majorization-Minimization Approach

In this paper, we present a novel optimization algorithm designed specifically for estimating state-space models to deal with heavy-tailed measurement noise and constraints. Our algorithm addresses two significant limitations found in existing approaches: susceptibility to measurement noise outliers and difficulties in incorporating constraints into state estimation. By formulating constrained state estimation as an optimization problem and employing the Majorization-Minimization (MM) approach, our framework provides a unified solution that enhances the robustness of the Kalman filter. Experimental results demonstrate high accuracy and computational efficiency achieved by our proposed approach, establishing it as a promising solution for robust and constrained state estimation in real-world applications.

The Informed Elastic Net for Fast Grouped Variable Selection and FDR Control in Genomics Research

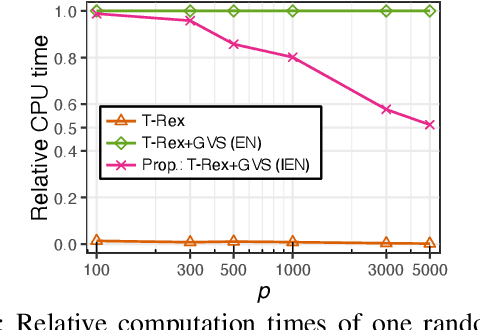
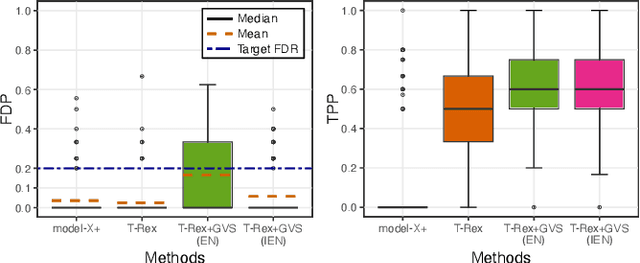
Modern genomics research relies on genome-wide association studies (GWAS) to identify the few genetic variants among potentially millions that are associated with diseases of interest. Only reproducible discoveries of groups of associations improve our understanding of complex polygenic diseases and enable the development of new drugs and personalized medicine. Thus, fast multivariate variable selection methods that have a high true positive rate (TPR) while controlling the false discovery rate (FDR) are crucial. Recently, the T-Rex+GVS selector, a version of the T-Rex selector that uses the elastic net (EN) as a base selector to perform grouped variable election, was proposed. Although it significantly increased the TPR in simulated GWAS compared to the original T-Rex, its comparably high computational cost limits scalability. Therefore, we propose the informed elastic net (IEN), a new base selector that significantly reduces computation time while retaining the grouped variable selection property. We quantify its grouping effect and derive its formulation as a Lasso-type optimization problem, which is solved efficiently within the T-Rex framework by the terminated LARS algorithm. Numerical simulations and a GWAS study demonstrate that the proposed T-Rex+GVS (IEN) exhibits the desired grouping effect, reduces computation time, and achieves the same TPR as T-Rex+GVS (EN) but with lower FDR, which makes it a promising method for large-scale GWAS.

Polynomial Graphical Lasso: Learning Edges from Gaussian Graph-Stationary Signals

This paper introduces Polynomial Graphical Lasso (PGL), a new approach to learning graph structures from nodal signals. Our key contribution lies in modeling the signals as Gaussian and stationary on the graph, enabling the development of a graph-learning formulation that combines the strengths of graphical lasso with a more encompassing model. Specifically, we assume that the precision matrix can take any polynomial form of the sought graph, allowing for increased flexibility in modeling nodal relationships. Given the resulting complexity and nonconvexity of the resulting optimization problem, we (i) propose a low-complexity algorithm that alternates between estimating the graph and precision matrices, and (ii) characterize its convergence. We evaluate the performance of PGL through comprehensive numerical simulations using both synthetic and real data, demonstrating its superiority over several alternatives. Overall, this approach presents a significant advancement in graph learning and holds promise for various applications in graph-aware signal analysis and beyond.

High-Dimensional False Discovery Rate Control for Dependent Variables

Algorithms that ensure reproducible findings from large-scale, high-dimensional data are pivotal in numerous signal processing applications. In recent years, multivariate false discovery rate (FDR) controlling methods have emerged, providing guarantees even in high-dimensional settings where the number of variables surpasses the number of samples. However, these methods often fail to reliably control the FDR in the presence of highly dependent variable groups, a common characteristic in fields such as genomics and finance. To tackle this critical issue, we introduce a novel framework that accounts for general dependency structures. Our proposed dependency-aware T-Rex selector integrates hierarchical graphical models within the T-Rex framework to effectively harness the dependency structure among variables. Leveraging martingale theory, we prove that our variable penalization mechanism ensures FDR control. We further generalize the FDR-controlling framework by stating and proving a clear condition necessary for designing both graphical and non-graphical models that capture dependencies. Additionally, we formulate a fully integrated optimal calibration algorithm that concurrently determines the parameters of the graphical model and the T-Rex framework, such that the FDR is controlled while maximizing the number of selected variables. Numerical experiments and a breast cancer survival analysis use-case demonstrate that the proposed method is the only one among the state-of-the-art benchmark methods that controls the FDR and reliably detects genes that have been previously identified to be related to breast cancer. An open-source implementation is available within the R package TRexSelector on CRAN.

FDR-Controlled Portfolio Optimization for Sparse Financial Index Tracking

In high-dimensional data analysis, such as financial index tracking or biomedical applications, it is crucial to select the few relevant variables while maintaining control over the false discovery rate (FDR). In these applications, strong dependencies often exist among the variables (e.g., stock returns), which can undermine the FDR control property of existing methods like the model-X knockoff method or the T-Rex selector. To address this issue, we have expanded the T-Rex framework to accommodate overlapping groups of highly correlated variables. This is achieved by integrating a nearest neighbors penalization mechanism into the framework, which provably controls the FDR at the user-defined target level. A real-world example of sparse index tracking demonstrates the proposed method's ability to accurately track the S&P 500 index over the past 20 years based on a small number of stocks. An open-source implementation is provided within the R package TRexSelector on CRAN.

Sparse PCA with False Discovery Rate Controlled Variable Selection

Sparse principal component analysis (PCA) aims at mapping large dimensional data to a linear subspace of lower dimension. By imposing loading vectors to be sparse, it performs the double duty of dimension reduction and variable selection. Sparse PCA algorithms are usually expressed as a trade-off between explained variance and sparsity of the loading vectors (i.e., number of selected variables). As a high explained variance is not necessarily synonymous with relevant information, these methods are prone to select irrelevant variables. To overcome this issue, we propose an alternative formulation of sparse PCA driven by the false discovery rate (FDR). We then leverage the Terminating-Random Experiments (T-Rex) selector to automatically determine an FDR-controlled support of the loading vectors. A major advantage of the resulting T-Rex PCA is that no sparsity parameter tuning is required. Numerical experiments and a stock market data example demonstrate a significant performance improvement.

Joint Signal Recovery and Graph Learning from Incomplete Time-Series

Learning a graph from data is the key to taking advantage of graph signal processing tools. Most of the conventional algorithms for graph learning require complete data statistics, which might not be available in some scenarios. In this work, we aim to learn a graph from incomplete time-series observations. From another viewpoint, we consider the problem of semi-blind recovery of time-varying graph signals where the underlying graph model is unknown. We propose an algorithm based on the method of block successive upperbound minimization (BSUM), for simultaneous inference of the signal and the graph from incomplete data. Simulation results on synthetic and real time-series demonstrate the performance of the proposed method for graph learning and signal recovery.