Jiaxi Ying
Time-Varying Graph Learning for Data with Heavy-Tailed Distribution
Dec 31, 2024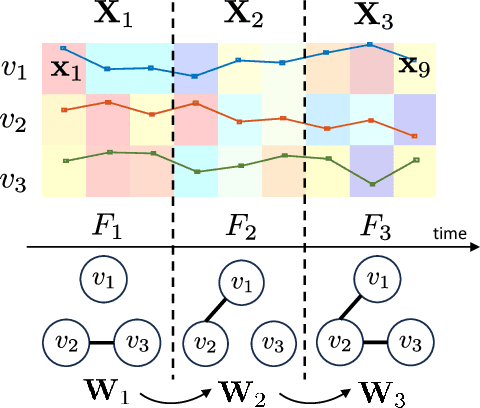
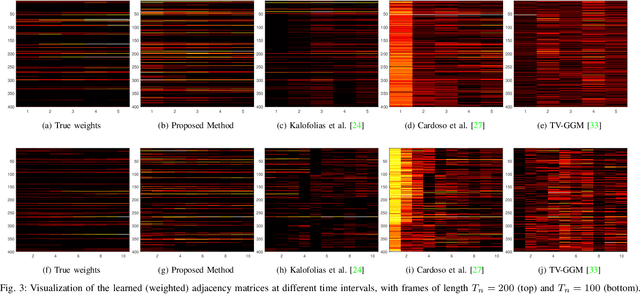
Abstract:Graph models provide efficient tools to capture the underlying structure of data defined over networks. Many real-world network topologies are subject to change over time. Learning to model the dynamic interactions between entities in such networks is known as time-varying graph learning. Current methodology for learning such models often lacks robustness to outliers in the data and fails to handle heavy-tailed distributions, a common feature in many real-world datasets (e.g., financial data). This paper addresses the problem of learning time-varying graph models capable of efficiently representing heavy-tailed data. Unlike traditional approaches, we incorporate graph structures with specific spectral properties to enhance data clustering in our model. Our proposed method, which can also deal with noise and missing values in the data, is based on a stochastic approach, where a non-negative vector auto-regressive (VAR) model captures the variations in the graph and a Student-t distribution models the signal originating from this underlying time-varying graph. We propose an iterative method to learn time-varying graph topologies within a semi-online framework where only a mini-batch of data is used to update the graph. Simulations with both synthetic and real datasets demonstrate the efficacy of our model in analyzing heavy-tailed data, particularly those found in financial markets.
Polynomial Graphical Lasso: Learning Edges from Gaussian Graph-Stationary Signals
Apr 03, 2024



Abstract:This paper introduces Polynomial Graphical Lasso (PGL), a new approach to learning graph structures from nodal signals. Our key contribution lies in modeling the signals as Gaussian and stationary on the graph, enabling the development of a graph-learning formulation that combines the strengths of graphical lasso with a more encompassing model. Specifically, we assume that the precision matrix can take any polynomial form of the sought graph, allowing for increased flexibility in modeling nodal relationships. Given the resulting complexity and nonconvexity of the resulting optimization problem, we (i) propose a low-complexity algorithm that alternates between estimating the graph and precision matrices, and (ii) characterize its convergence. We evaluate the performance of PGL through comprehensive numerical simulations using both synthetic and real data, demonstrating its superiority over several alternatives. Overall, this approach presents a significant advancement in graph learning and holds promise for various applications in graph-aware signal analysis and beyond.
Learning Large-Scale MTP$_2$ Gaussian Graphical Models via Bridge-Block Decomposition
Sep 29, 2023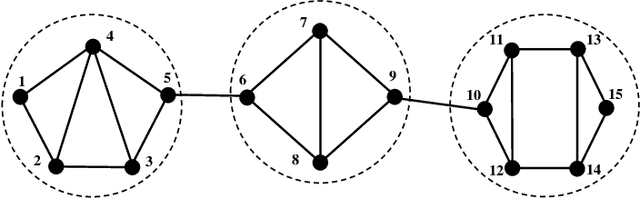

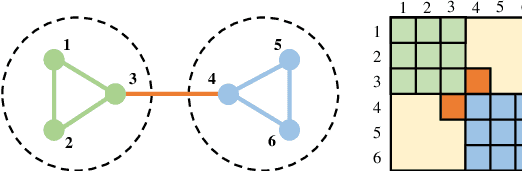
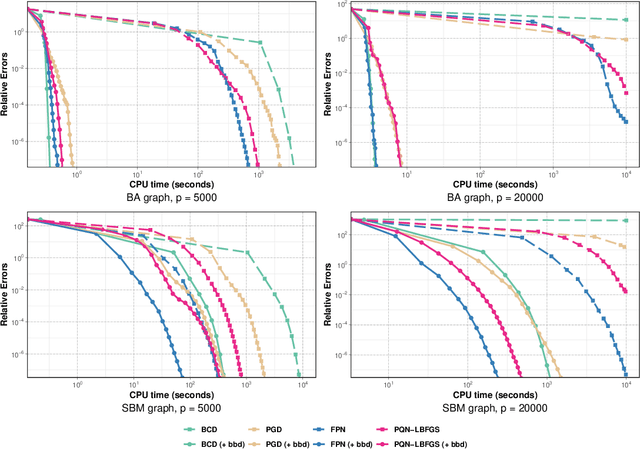
Abstract:This paper studies the problem of learning the large-scale Gaussian graphical models that are multivariate totally positive of order two ($\text{MTP}_2$). By introducing the concept of bridge, which commonly exists in large-scale sparse graphs, we show that the entire problem can be equivalently optimized through (1) several smaller-scaled sub-problems induced by a \emph{bridge-block decomposition} on the thresholded sample covariance graph and (2) a set of explicit solutions on entries corresponding to bridges. From practical aspect, this simple and provable discipline can be applied to break down a large problem into small tractable ones, leading to enormous reduction on the computational complexity and substantial improvements for all existing algorithms. The synthetic and real-world experiments demonstrate that our proposed method presents a significant speed-up compared to the state-of-the-art benchmarks.
Network Topology Inference with Sparsity and Laplacian Constraints
Sep 02, 2023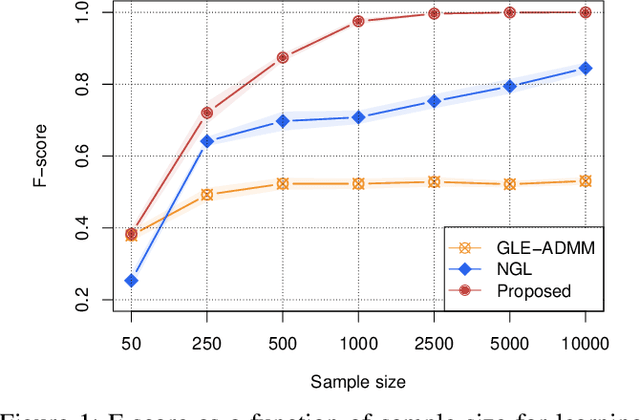
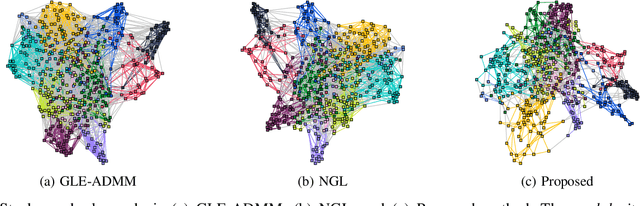
Abstract:We tackle the network topology inference problem by utilizing Laplacian constrained Gaussian graphical models, which recast the task as estimating a precision matrix in the form of a graph Laplacian. Recent research \cite{ying2020nonconvex} has uncovered the limitations of the widely used $\ell_1$-norm in learning sparse graphs under this model: empirically, the number of nonzero entries in the solution grows with the regularization parameter of the $\ell_1$-norm; theoretically, a large regularization parameter leads to a fully connected (densest) graph. To overcome these challenges, we propose a graph Laplacian estimation method incorporating the $\ell_0$-norm constraint. An efficient gradient projection algorithm is developed to solve the resulting optimization problem, characterized by sparsity and Laplacian constraints. Through numerical experiments with synthetic and financial time-series datasets, we demonstrate the effectiveness of the proposed method in network topology inference.
Adaptive Estimation of $\text{MTP}_2$ Graphical Models
Oct 27, 2022



Abstract:We consider the problem of estimating (diagonally dominant) M-matrices as precision matrices in Gaussian graphical models. Such models have received increasing attention in recent years, and have shown interesting properties, e.g., the maximum likelihood estimator exists with as little as two observations regardless of the underlying dimension. In this paper, we propose an adaptive estimation method, which consists of multiple stages: In the first stage, we solve an $\ell_1$-regularized maximum likelihood estimation problem, which leads to an initial estimate; in the subsequent stages, we iteratively refine the initial estimate by solving a sequence of weighted $\ell_1$-regularized problems. We further establish the theoretical guarantees on the estimation error, which consists of optimization error and statistical error. The optimization error decays to zero at a linear rate, indicating that the estimate is refined iteratively in subsequent stages, and the statistical error characterizes the statistical rate. The proposed method outperforms state-of-the-art methods in estimating precision matrices and identifying graph edges, as evidenced by synthetic and financial time-series data sets.
Efficient and Scalable High-Order Portfolios Design via Parametric Skew-t Distribution
Jun 06, 2022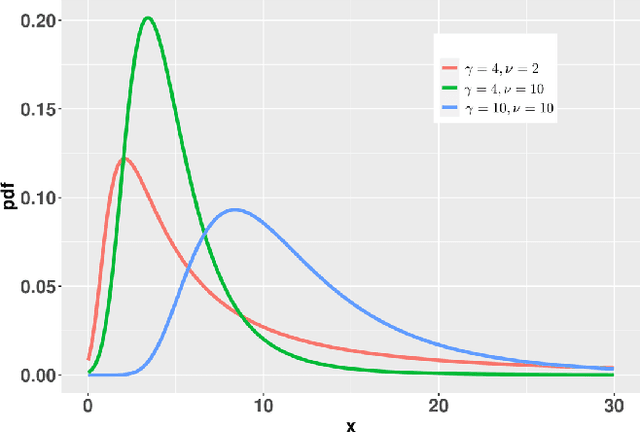
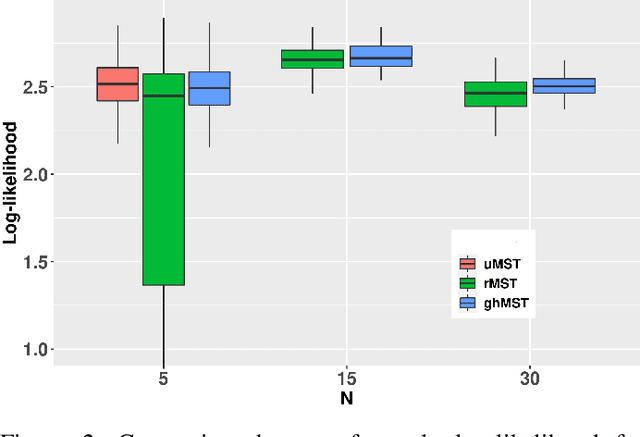
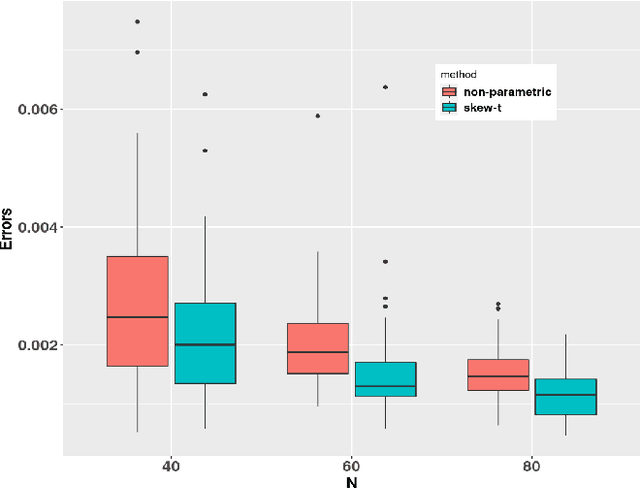
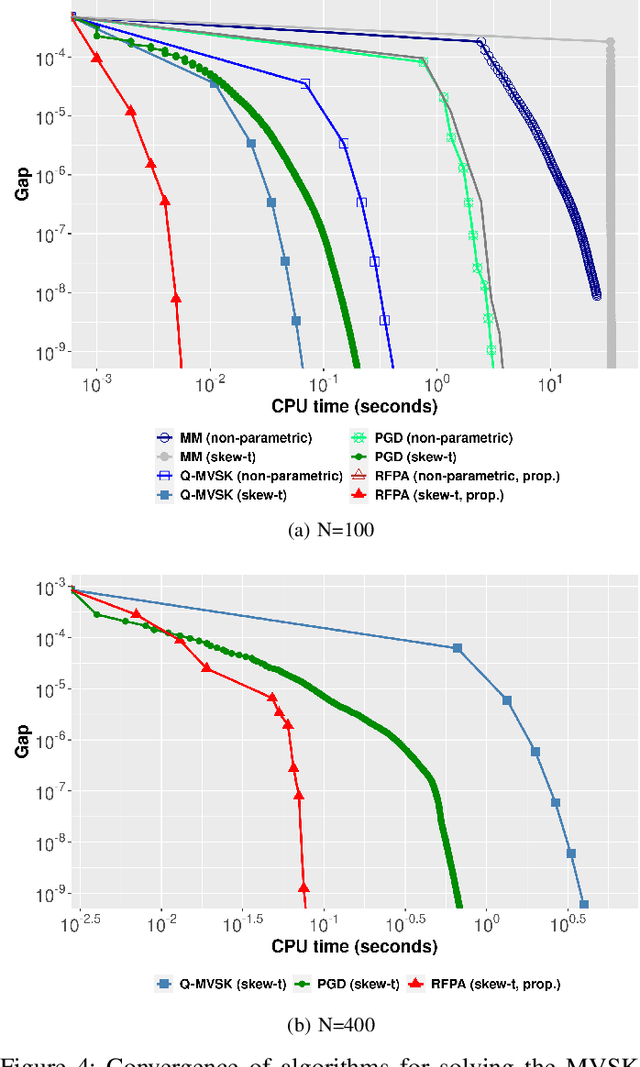
Abstract:Since Markowitz's mean-variance framework, optimizing a portfolio that maximizes the profit and minimizes the risk has been ubiquitous in the financial industry. Initially, profit and risk were measured by the first two moments of the portfolio's return, a.k.a. the mean and variance, which are sufficient to characterize a Gaussian distribution. However, it is broadly believed that the first two moments are not enough to capture the characteristics of the returns' behavior, which have been recognized to be asymmetric and heavy-tailed. Although there is ample evidence that portfolio designs involving the third and fourth moments, i.e., skewness and kurtosis, will outperform the conventional mean-variance framework, they are non-trivial. Specifically, in the classical framework, the memory and computational cost of computing the skewness and kurtosis grow sharply with the number of assets. To alleviate the difficulty in high-dimensional problems, we consider an alternative expression for high-order moments based on parametric representations via a generalized hyperbolic skew-t distribution. Then, we reformulate the high-order portfolio optimization problem as a fixed-point problem and propose a robust fixed-point acceleration algorithm that solves the problem in an efficient and scalable manner. Empirical experiments also demonstrate that our proposed high-order portfolio optimization framework is of low complexity and significantly outperforms the state-of-the-art methods by 2 to 4 orders of magnitude.
Fast Projected Newton-like Method for Precision Matrix Estimation with Nonnegative Partial Correlations
Dec 12, 2021



Abstract:We study the problem of estimating precision matrices in multivariate Gaussian distributions where all partial correlations are nonnegative, also known as multivariate totally positive of order two ($\mathrm{MTP}_2$). Such models have received significant attention in recent years, primarily due to interesting properties, e.g., the maximum likelihood estimator exists with as few as two observations regardless of the underlying dimension. We formulate this problem as a weighted $\ell_1$-norm regularized Gaussian maximum likelihood estimation under $\mathrm{MTP}_2$ constraints. On this direction, we propose a novel projected Newton-like algorithm that incorporates a well-designed approximate Newton direction, which results in our algorithm having the same orders of computation and memory costs as those of first-order methods. We prove that the proposed projected Newton-like algorithm converges to the minimizer of the problem. We further show, both theoretically and experimentally, that the minimizer of our formulation using the weighted $\ell_1$-norm is able to recover the support of the underlying precision matrix correctly without requiring the incoherence condition present in $\ell_1$-norm based methods. Experiments involving synthetic and real-world data demonstrate that our proposed algorithm is significantly more efficient, from a computational time perspective, than the state-of-the-art methods. Finally, we apply our method in financial time-series data, which are well-known for displaying positive dependencies, where we observe a significant performance in terms of modularity value on the learned financial networks.
Algorithms for Learning Graphs in Financial Markets
Dec 31, 2020



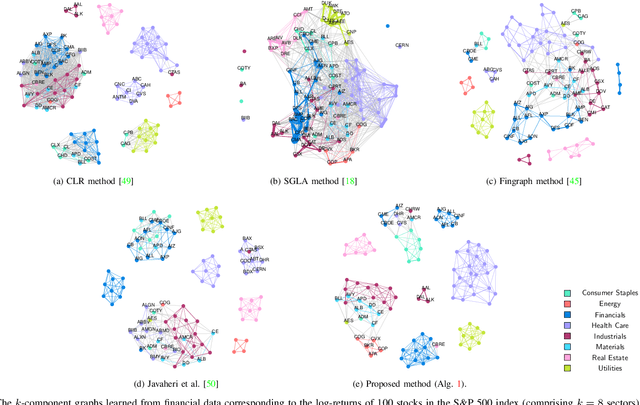
Abstract:In the past two decades, the field of applied finance has tremendously benefited from graph theory. As a result, novel methods ranging from asset network estimation to hierarchical asset selection and portfolio allocation are now part of practitioners' toolboxes. In this paper, we investigate the fundamental problem of learning undirected graphical models under Laplacian structural constraints from the point of view of financial market times series data. In particular, we present natural justifications, supported by empirical evidence, for the usage of the Laplacian matrix as a model for the precision matrix of financial assets, while also establishing a direct link that reveals how Laplacian constraints are coupled to meaningful physical interpretations related to the market index factor and to conditional correlations between stocks. Those interpretations lead to a set of guidelines that practitioners should be aware of when estimating graphs in financial markets. In addition, we design numerical algorithms based on the alternating direction method of multipliers to learn undirected, weighted graphs that take into account stylized facts that are intrinsic to financial data such as heavy tails and modularity. We illustrate how to leverage the learned graphs into practical scenarios such as stock time series clustering and foreign exchange network estimation. The proposed graph learning algorithms outperform the state-of-the-art methods in an extensive set of practical experiments. Furthermore, we obtain theoretical and empirical convergence results for the proposed algorithms. Along with the developed methodologies for graph learning in financial markets, we release an R package, called fingraph, accommodating the code and data to obtain all the experimental results.
Does the $\ell_1$-norm Learn a Sparse Graph under Laplacian Constrained Graphical Models?
Jun 26, 2020



Abstract:We consider the problem of learning a sparse graph under Laplacian constrained Gaussian graphical models. This problem can be formulated as a penalized maximum likelihood estimation of the precision matrix under Laplacian structural constraints. Like in the classical graphical lasso problem, recent works made use of the $\ell_1$-norm regularization with the goal of promoting sparsity in Laplacian structural precision matrix estimation. However, we find that the widely used $\ell_1$-norm is not effective in imposing a sparse solution in this problem. Through empirical evidence, we observe that the number of nonzero graph weights grows with the increase of the regularization parameter. From a theoretical perspective, we prove that a large regularization parameter will surprisingly lead to a fully connected graph. To address this issue, we propose a nonconvex estimation method by solving a sequence of weighted $\ell_1$-norm penalized sub-problems and prove that the statistical error of the proposed estimator matches the minimax lower bound. To solve each sub-problem, we develop a projected gradient descent algorithm that enjoys a linear convergence rate. Numerical experiments involving synthetic and real-world data sets from the recent COVID-19 pandemic and financial stock markets demonstrate the effectiveness of the proposed method. An open source $\mathsf{R}$ package containing the code for all the experiments is available at https://github.com/mirca/sparseGraph.
Structured Graph Learning Via Laplacian Spectral Constraints
Sep 24, 2019

Abstract:Learning a graph with a specific structure is essential for interpretability and identification of the relationships among data. It is well known that structured graph learning from observed samples is an NP-hard combinatorial problem. In this paper, we first show that for a set of important graph families it is possible to convert the structural constraints of structure into eigenvalue constraints of the graph Laplacian matrix. Then we introduce a unified graph learning framework, lying at the integration of the spectral properties of the Laplacian matrix with Gaussian graphical modeling that is capable of learning structures of a large class of graph families. The proposed algorithms are provably convergent and practically amenable for large-scale semi-supervised and unsupervised graph-based learning tasks. Extensive numerical experiments with both synthetic and real data sets demonstrate the effectiveness of the proposed methods. An R package containing code for all the experimental results is available at https://cran.r-project.org/package=spectralGraphTopology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge