Amirhossein Javaheri
Clustering of Incomplete Data via a Bipartite Graph Structure
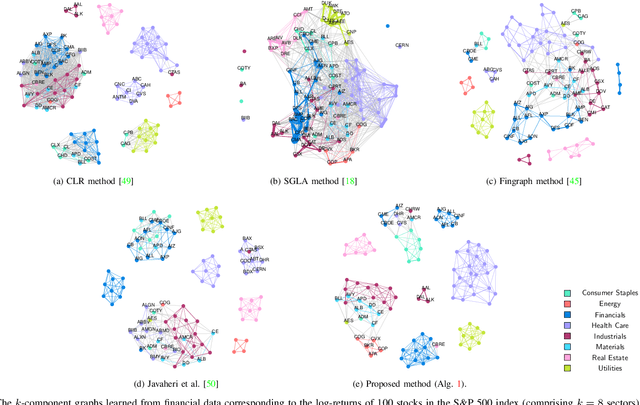
May 13, 2025Abstract:There are various approaches to graph learning for data clustering, incorporating different spectral and structural constraints through diverse graph structures. Some methods rely on bipartite graph models, where nodes are divided into two classes: centers and members. These models typically require access to data for the center nodes in addition to observations from the member nodes. However, such additional data may not always be available in many practical scenarios. Moreover, popular Gaussian models for graph learning have demonstrated limited effectiveness in modeling data with heavy-tailed distributions, which are common in financial markets. In this paper, we propose a clustering method based on a bipartite graph model that addresses these challenges. First, it can infer clusters from incomplete data without requiring information about the center nodes. Second, it is designed to effectively handle heavy-tailed data. Numerical experiments using real financial data validate the efficiency of the proposed method for data clustering.
Time-Varying Graph Learning for Data with Heavy-Tailed Distribution
Dec 31, 2024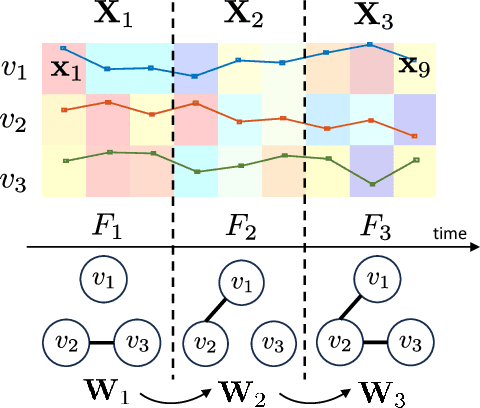
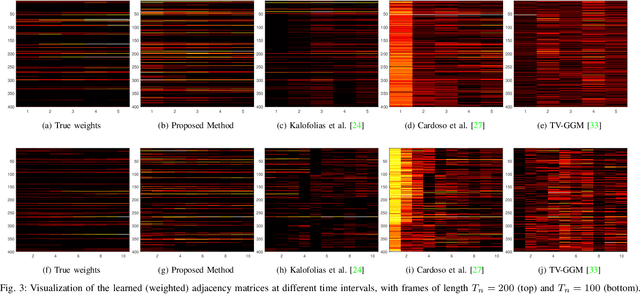
Abstract:Graph models provide efficient tools to capture the underlying structure of data defined over networks. Many real-world network topologies are subject to change over time. Learning to model the dynamic interactions between entities in such networks is known as time-varying graph learning. Current methodology for learning such models often lacks robustness to outliers in the data and fails to handle heavy-tailed distributions, a common feature in many real-world datasets (e.g., financial data). This paper addresses the problem of learning time-varying graph models capable of efficiently representing heavy-tailed data. Unlike traditional approaches, we incorporate graph structures with specific spectral properties to enhance data clustering in our model. Our proposed method, which can also deal with noise and missing values in the data, is based on a stochastic approach, where a non-negative vector auto-regressive (VAR) model captures the variations in the graph and a Student-t distribution models the signal originating from this underlying time-varying graph. We propose an iterative method to learn time-varying graph topologies within a semi-online framework where only a mini-batch of data is used to update the graph. Simulations with both synthetic and real datasets demonstrate the efficacy of our model in analyzing heavy-tailed data, particularly those found in financial markets.
Joint Signal Recovery and Graph Learning from Incomplete Time-Series
Dec 28, 2023


Abstract:Learning a graph from data is the key to taking advantage of graph signal processing tools. Most of the conventional algorithms for graph learning require complete data statistics, which might not be available in some scenarios. In this work, we aim to learn a graph from incomplete time-series observations. From another viewpoint, we consider the problem of semi-blind recovery of time-varying graph signals where the underlying graph model is unknown. We propose an algorithm based on the method of block successive upperbound minimization (BSUM), for simultaneous inference of the signal and the graph from incomplete data. Simulation results on synthetic and real time-series demonstrate the performance of the proposed method for graph learning and signal recovery.
Impulsive Noise Robust Sparse Recovery via Continuous Mixed Norm
Apr 12, 2018



Abstract:This paper investigates the problem of sparse signal recovery in the presence of additive impulsive noise. The heavytailed impulsive noise is well modelled with stable distributions. Since there is no explicit formulation for the probability density function of $S\alpha S$ distribution, alternative approximations like Generalized Gaussian Distribution (GGD) are used which impose $\ell_p$-norm fidelity on the residual error. In this paper, we exploit a Continuous Mixed Norm (CMN) for robust sparse recovery instead of $\ell_p$-norm. We show that in blind conditions, i.e., in case where the parameters of noise distribution are unknown, incorporating CMN can lead to near optimal recovery. We apply Alternating Direction Method of Multipliers (ADMM) for solving the problem induced by utilizing CMN for robust sparse recovery. In this approach, CMN is replaced with a surrogate function and Majorization-Minimization technique is incorporated to solve the problem. Simulation results confirm the efficiency of the proposed method compared to some recent algorithms in the literature for impulsive noise robust sparse recovery.
A Convex Similarity Index for Sparse Recovery of Missing Image Samples
Oct 17, 2017



Abstract:This paper investigates the problem of recovering missing samples using methods based on sparse representation adapted especially for image signals. Instead of $l_2$-norm or Mean Square Error (MSE), a new perceptual quality measure is used as the similarity criterion between the original and the reconstructed images. The proposed criterion called Convex SIMilarity (CSIM) index is a modified version of the Structural SIMilarity (SSIM) index, which despite its predecessor, is convex and uni-modal. We derive mathematical properties for the proposed index and show how to optimally choose the parameters of the proposed criterion, investigating the Restricted Isometry (RIP) and error-sensitivity properties. We also propose an iterative sparse recovery method based on a constrained $l_1$-norm minimization problem, incorporating CSIM as the fidelity criterion. The resulting convex optimization problem is solved via an algorithm based on Alternating Direction Method of Multipliers (ADMM). Taking advantage of the convexity of the CSIM index, we also prove the convergence of the algorithm to the globally optimal solution of the proposed optimization problem, starting from any arbitrary point. Simulation results confirm the performance of the new similarity index as well as the proposed algorithm for missing sample recovery of image patch signals.
Recovery of Missing Samples Using Sparse Approximation via a Convex Similarity Measure
Jun 28, 2017


Abstract:In this paper, we study the missing sample recovery problem using methods based on sparse approximation. In this regard, we investigate the algorithms used for solving the inverse problem associated with the restoration of missed samples of image signal. This problem is also known as inpainting in the context of image processing and for this purpose, we suggest an iterative sparse recovery algorithm based on constrained $l_1$-norm minimization with a new fidelity metric. The proposed metric called Convex SIMilarity (CSIM) index, is a simplified version of the Structural SIMilarity (SSIM) index, which is convex and error-sensitive. The optimization problem incorporating this criterion, is then solved via Alternating Direction Method of Multipliers (ADMM). Simulation results show the efficiency of the proposed method for missing sample recovery of 1D patch vectors and inpainting of 2D image signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge