Joint Signal Recovery and Graph Learning from Incomplete Time-Series

Learning a graph from data is the key to taking advantage of graph signal processing tools. Most of the conventional algorithms for graph learning require complete data statistics, which might not be available in some scenarios. In this work, we aim to learn a graph from incomplete time-series observations. From another viewpoint, we consider the problem of semi-blind recovery of time-varying graph signals where the underlying graph model is unknown. We propose an algorithm based on the method of block successive upperbound minimization (BSUM), for simultaneous inference of the signal and the graph from incomplete data. Simulation results on synthetic and real time-series demonstrate the performance of the proposed method for graph learning and signal recovery.

Distributed Estimation with Partially Accessible Information: An IMAT Approach to LMS Diffusion

Distributed algorithms, particularly Diffusion Least Mean Square, are widely favored for their reliability, robustness, and fast convergence in various industries. However, limited observability of the target can compromise the integrity of the algorithm. To address this issue, this paper proposes a framework for analyzing combination strategies by drawing inspiration from signal flow analysis. A thresholding-based algorithm is also presented to identify and utilize the support vector in scenarios with missing information about the target vector's support. The proposed approach is demonstrated in two combination scenarios, showcasing the effectiveness of the algorithm in situations characterized by sparse observations in the time and transform domains.

Non-Orthogonal Time-Frequency Space Modulation

This paper proposes a Time-Frequency Space Transformation (TFST) to derive non-orthogonal bases for modulation techniques over the delay-doppler plane. A family of Overloaded Delay-Doppler Modulation (ODDM) techniques is proposed based on the TFST, which enhances flexibility and efficiency by expressing modulated signals as a linear combination of basis signals. A Non-Orthogonal Time-Frequency Space (NOTFS) digital modulation is derived for the proposed ODDM techniques, and simulations show that they offer high-mobility communication systems with improved spectral efficiency and low latency, particularly in challenging scenarios such as high overloading factors and Additive White Gaussian Noise (AWGN) channels. A modified sphere decoding algorithm is also presented to efficiently decode the received signal. The proposed modulation and decoding techniques contribute to the advancement of non-orthogonal approaches in the next-generation of mobile communication systems, delivering superior spectral efficiency and low latency, and offering a promising solution towards the development of efficient high-mobility communication systems.

Enhancing the SEFDM Performance in High-Doppler Channels

In this paper, we propose the use of Spectrally Efficient Frequency Division Multiplexing (SEFDM) with additional techniques such as Frequency Domain Cyclic Prefix (FDCP) and Modified Non-Linear (MNL) acceleration for efficient handling of the impact of delay and Doppler shift in mobile communication channels. Our approach exhibits superior performance and spectral efficiency in comparison to traditional communication systems, while maintaining low computational cost. We study a model of the SEFDM communication system and investigate the impact of MNL acceleration with soft and hard decision Inverse System on the performance of SEFDM detection in the AWGN channel. We also analyze the effectiveness of FDCP in compensating for the impact of Doppler shift, and report BER detection figures using Regularized Sphere Decoding in various simulation scenarios. Our simulations demonstrate that it is possible to achieve acceptable performance in Doppler channels while maintaining the superiority of SEFDM over OFDM in terms of spectral efficiency. The results suggest that our proposed approach can tackle the effects of delay and Doppler shift in mobile communication networks, guaranteeing dependable and high-quality communication even in extremely challenging environments.

Algorithmic Trading Using Continuous Action Space Deep Reinforcement Learning

Price movement prediction has always been one of the traders' concerns in financial market trading. In order to increase their profit, they can analyze the historical data and predict the price movement. The large size of the data and complex relations between them lead us to use algorithmic trading and artificial intelligence. This paper aims to offer an approach using Twin-Delayed DDPG (TD3) and the daily close price in order to achieve a trading strategy in the stock and cryptocurrency markets. Unlike previous studies using a discrete action space reinforcement learning algorithm, the TD3 is continuous, offering both position and the number of trading shares. Both the stock (Amazon) and cryptocurrency (Bitcoin) markets are addressed in this research to evaluate the performance of the proposed algorithm. The achieved strategy using the TD3 is compared with some algorithms using technical analysis, reinforcement learning, stochastic, and deterministic strategies through two standard metrics, Return and Sharpe ratio. The results indicate that employing both position and the number of trading shares can improve the performance of a trading system based on the mentioned metrics.

Robust Adaptive Generalized Correntropy-based Smoothed Graph Signal Recovery with a Kernel Width Learning

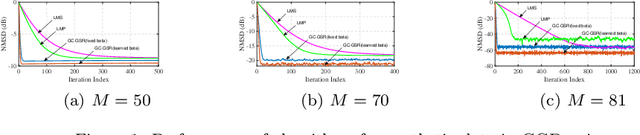
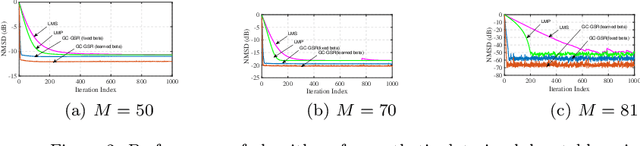
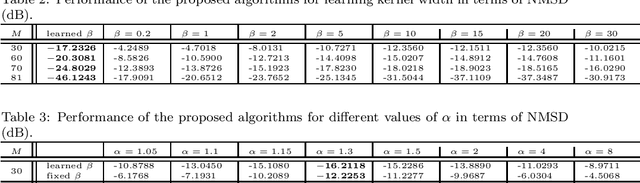
This paper proposes a robust adaptive algorithm for smooth graph signal recovery which is based on generalized correntropy. A proper cost function is defined for this purpose. The proposed algorithm is derived and a kernel width learning-based version of the algorithm is suggested which the simulation results show the superiority of it to the fixed correntropy kernel version of the algorithm. Moreover, some theoretical analysis of the proposed algorithm are provided. In this regard, firstly, the convexity analysis of the cost function is discussed. Secondly, the uniform stability of the algorithm is investigated. Thirdly, the mean convergence analysis is also added. Finally, the complexity analysis of the algorithm is incorporated. In addition, some synthetic and real-world experiments show the advantage of the proposed algorithm in comparison to some other adaptive algorithms in the literature of adaptive graph signal recovery.

Ensemble Neural Representation Networks

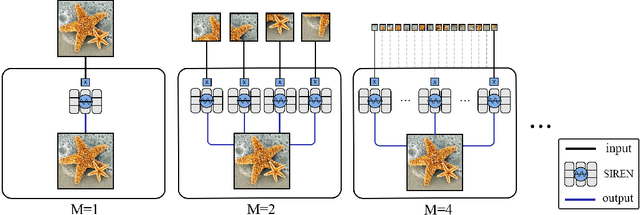
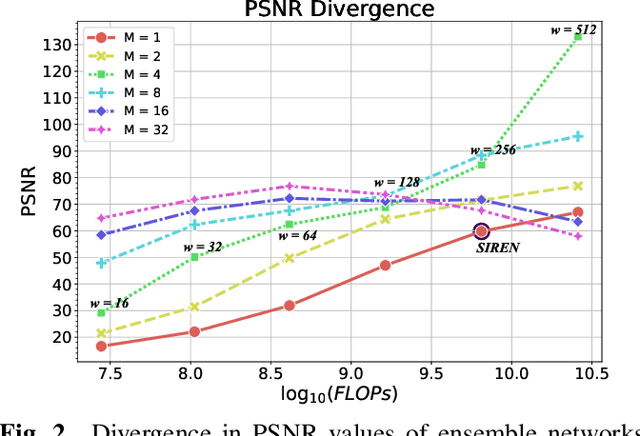
Implicit Neural Representation (INR) has recently attracted considerable attention for storing various types of signals in continuous forms. The existing INR networks require lengthy training processes and high-performance computational resources. In this paper, we propose a novel sub-optimal ensemble architecture for INR that resolves the aforementioned problems. In this architecture, the representation task is divided into several sub-tasks done by independent sub-networks. We show that the performance of the proposed ensemble INR architecture may decrease if the dimensions of sub-networks increase. Hence, it is vital to suggest an optimization algorithm to find the sub-optimal structure of the ensemble network, which is done in this paper. According to the simulation results, the proposed architecture not only has significantly fewer floating-point operations (FLOPs) and less training time, but it also has better performance in terms of Peak Signal to Noise Ratio (PSNR) compared to those of its counterparts.

Efficient Sparse Artificial Neural Networks

The brain, as the source of inspiration for Artificial Neural Networks (ANN), is based on a sparse structure. This sparse structure helps the brain to consume less energy, learn easier and generalize patterns better than any other ANN. In this paper, two evolutionary methods for adopting sparsity to ANNs are proposed. In the proposed methods, the sparse structure of a network as well as the values of its parameters are trained and updated during the learning process. The simulation results show that these two methods have better accuracy and faster convergence while they need fewer training samples compared to their sparse and non-sparse counterparts. Furthermore, the proposed methods significantly improve the generalization power and reduce the number of parameters. For example, the sparsification of the ResNet47 network by exploiting our proposed methods for the image classification of ImageNet dataset uses 40 % fewer parameters while the top-1 accuracy of the model improves by 12% and 5% compared to the dense network and their sparse counterpart, respectively. As another example, the proposed methods for the CIFAR10 dataset converge to their final structure 7 times faster than its sparse counterpart, while the final accuracy increases by 6%.

Distributed interference cancellation in multi-agent scenarios

This paper considers the problem of detecting impaired and noisy nodes over network. In a distributed algorithm, lots of processing units are incorporating and communicating with each other to reach a global goal. Due to each one's state in the shared environment, they can help the other nodes or mislead them (due to noise or a deliberate attempt). Previous works mainly focused on proper locating agents and weight assignment based on initial environment state to minimize malfunctioning of noisy nodes. We propose an algorithm to be able to adapt sharing weights according to behavior of the agents. Applying the introduced algorithm to a multi-agent RL scenario and the well-known diffusion LMS demonstrates its capability and generality.

A Nonlinear Acceleration Method for Iterative Algorithms

Iterative methods have led to better understanding and solving problems such as missing sampling, deconvolution, inverse systems, impulsive and Salt and Pepper noise removal problems. However, the challenges such as the speed of convergence and or the accuracy of the answer still remain. In order to improve the existing iterative algorithms, a non-linear method is discussed in this paper. The mentioned method is analyzed from different aspects, including its convergence and its ability to accelerate recursive algorithms. We show that this method is capable of improving Iterative Method (IM) as a non-uniform sampling reconstruction algorithm and some iterative sparse recovery algorithms such as Iterative Reweighted Least Squares (IRLS), Iterative Method with Adaptive Thresholding (IMAT), Smoothed l0 (SL0) and Alternating Direction Method of Multipliers (ADMM) for solving LASSO problems family (including Lasso itself, Lasso-LSQR and group-Lasso). It is also capable of both accelerating and stabilizing the well-known Chebyshev Acceleration (CA) method. Furthermore, the proposed algorithm can extend the stability range by reducing the sensitivity of iterative algorithms to the changes of adaptation rate.