Robust Adaptive Generalized Correntropy-based Smoothed Graph Signal Recovery with a Kernel Width Learning
Paper and Code
Sep 19, 2022
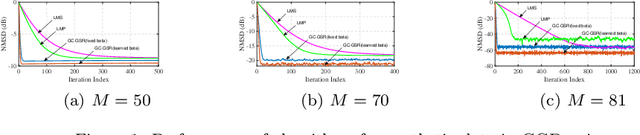
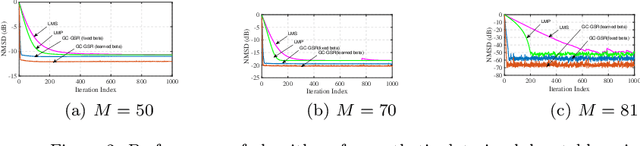
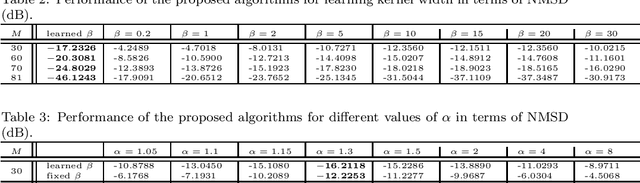
This paper proposes a robust adaptive algorithm for smooth graph signal recovery which is based on generalized correntropy. A proper cost function is defined for this purpose. The proposed algorithm is derived and a kernel width learning-based version of the algorithm is suggested which the simulation results show the superiority of it to the fixed correntropy kernel version of the algorithm. Moreover, some theoretical analysis of the proposed algorithm are provided. In this regard, firstly, the convexity analysis of the cost function is discussed. Secondly, the uniform stability of the algorithm is investigated. Thirdly, the mean convergence analysis is also added. Finally, the complexity analysis of the algorithm is incorporated. In addition, some synthetic and real-world experiments show the advantage of the proposed algorithm in comparison to some other adaptive algorithms in the literature of adaptive graph signal recovery.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge