Markovian Block Sparse Signal Detection Using One Bit Measurements

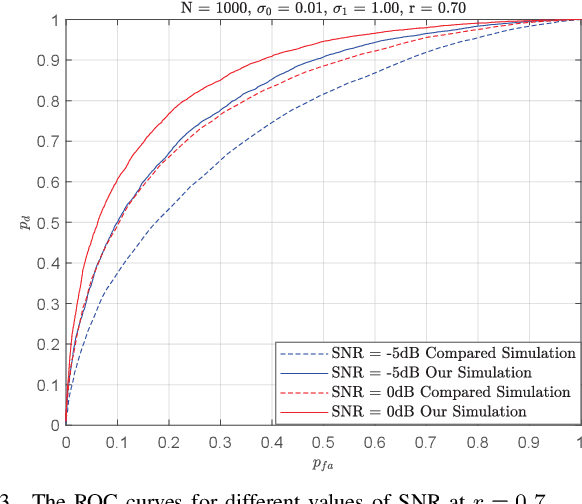
This paper presents a novel sparse signal detection scheme designed for a correlated Markovian Bernoulli-Gaussian sparse signal model, which can equivalently be viewed as a block sparse signal model. Despite the inherent complexity of the model, our approach yields a closed-form detection criterion. Theoretical analyses of the proposed detector are provided, including the computation of false alarm probability and detection probability through closed-form formulas. Simulation results compellingly demonstrate the advantages of our proposed detector compared to an existing detector in the literature.

Double-Private Distributed Estimation Algorithm Using Differential Privacy and a Key-Like Proportionate Matrix with Its Performance Analysis

In this brief, we present an enhanced privacy-preserving distributed estimation algorithm, referred to as the ``Double-Private Algorithm," which combines the principles of both differential privacy (DP) and cryptography. The proposed algorithm enhances privacy by introducing DP noise into the intermediate estimations of neighboring nodes. Additionally, we employ an inverse of a closed-form reproducible proportionate gain matrix as the cryptographic key matrix to fortify the privacy protection within the proposed double private algorithm. \textcolor{blue}{We improve the algorithm by transmitting alternative variable vectors instead of raw measurements, resulting in enhanced key matrix reconstruction performance. This innovative approach mitigate noise impact, enhancing overall algorithm effectiveness.} We also establish an upper bound for the norm of the error between the non-private Diffusion Least Mean Square (DLMS) algorithm and our double private algorithm. Further, we determine a sufficient condition for the step-size to ensure the mean convergence of the proposed algorithm. Simulation results demonstrate the effectiveness of the proposed algorithm, particularly its ability to attain the final Mean Square Deviation (MSD) comparable to that of the non-private DLMS.

Second-Order Nonlinearity Estimated and Compensated Diffusion LMS Algorithm: Theoretical Upper Bound, Cramer-Rao Lower bound, and Convergence Analysis

In this paper, an algorithm for estimation and compensation of second-order nonlinearity in wireless sensor setwork (WSN) in distributed estimation framework is proposed. First, the effect of second-order nonlinearity on the performance of Diffusion Least Mean Square (DLMS) algorithm is investigated and an upper bound for $l^2$-norm of the error due to nonlinearity is derived mathematically. Second, mean convergence analysis of the DLMS algorithm in presence of second-order nonlinearity is derived. Third, a distributed algorithm is suggested which consists of extra nonlinearity estimation and compensation units. Moreover, considering the second-order nonlinearity, the Cramer-Rao bound (CRB) for estimating both the unknown vector and nonlinearity coefficient vector is calculated, in which the Fisher information matrix is obtained in a closed-form formula. Simulation results demonstrate the effectiveness of the proposed algorithm in improving the performance of distributed estimation in the presence of nonlinear sensors in a WSN.

Proportionate Adaptive Graph Signal Recovery

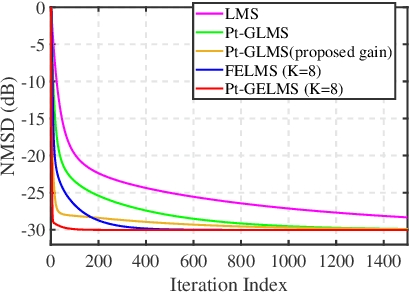
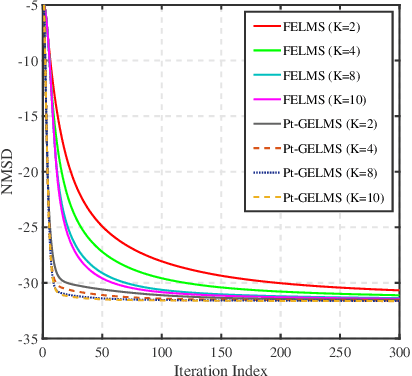
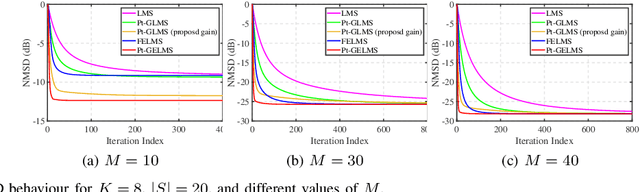
This paper generalizes the proportionate-type adaptive algorithm to the graph signal processing and proposes two proportionate-type adaptive graph signal recovery algorithms. The gain matrix of the proportionate algorithm leads to faster convergence than least mean squares (LMS) algorithm. In this paper, the gain matrix is obtained in a closed-form by minimizing the gradient of the mean-square deviation (GMSD). The first algorithm is the Proportionate-type Graph LMS (Pt-GLMS) algorithm which simply uses a gain matrix in the recursion process of the LMS algorithm and accelerates the convergence of the Pt-GLMS algorithm compared to the LMS algorithm. The second algorithm is the Proportionate-type Graph Extended LMS (Pt-GELMS) algorithm, which uses the previous signal vectors alongside the signal of the current iteration. The Pt-GELMS algorithm utilizes two gain matrices to control the effect of the signal of the previous iterations. The stability analyses of the algorithms are also provided. Simulation results demonstrate the efficacy of the two proposed proportionate-type LMS algorithms.

Robust Adaptive Generalized Correntropy-based Smoothed Graph Signal Recovery with a Kernel Width Learning

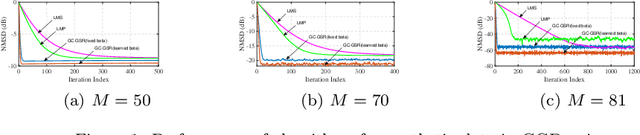
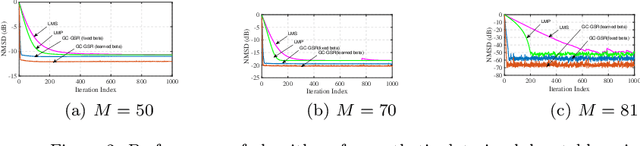
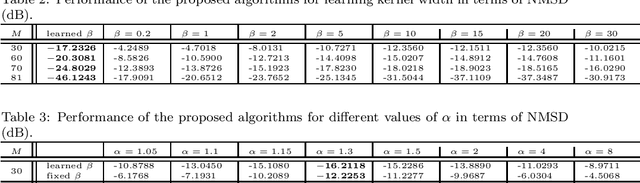
This paper proposes a robust adaptive algorithm for smooth graph signal recovery which is based on generalized correntropy. A proper cost function is defined for this purpose. The proposed algorithm is derived and a kernel width learning-based version of the algorithm is suggested which the simulation results show the superiority of it to the fixed correntropy kernel version of the algorithm. Moreover, some theoretical analysis of the proposed algorithm are provided. In this regard, firstly, the convexity analysis of the cost function is discussed. Secondly, the uniform stability of the algorithm is investigated. Thirdly, the mean convergence analysis is also added. Finally, the complexity analysis of the algorithm is incorporated. In addition, some synthetic and real-world experiments show the advantage of the proposed algorithm in comparison to some other adaptive algorithms in the literature of adaptive graph signal recovery.

Spectral Unmixing of Hyperspectral Images Based on Block Sparse Structure

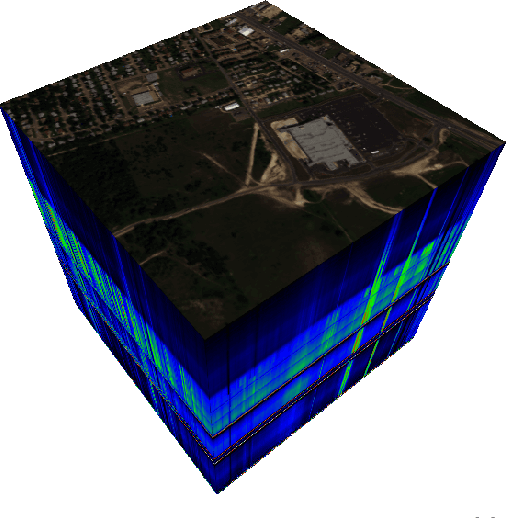
Spectral unmixing (SU) of hyperspectral images (HSIs) is one of the important areas in remote sensing (RS) that needs to be carefully addressed in different RS applications. Despite the high spectral resolution of the hyperspectral data, the relatively low spatial resolution of the sensors may lead to mixture of different pure materials within the image pixels. In this case, the spectrum of a given pixel recorded by the sensor can be a combination of multiple spectra each belonging to a unique material in that pixel. Spectral unmixing is then used as a technique to extract the spectral characteristics of the different materials within the mixed pixels and to recover the spectrum of each pure spectral signature, called endmember. Block-sparsity exists in hyperspectral images as a result of spectral similarity between neighboring pixels. In block-sparse signals, the nonzero samples occur in clusters and the pattern of the clusters is often supposed to be unavailable as prior information. This paper presents an innovative spectral unmixing approach for HSIs based on block-sparse structure and sparse Bayesian learning (SBL) strategy. To evaluate the performance of the proposed SU algorithm, it is tested on both synthetic and real hyperspectral data and the quantitative results are compared to those of other state-of-the-art methods in terms of abundance angel distance (AAD) and mean square error (MSE). The achieved results show the superiority of the proposed algorithm over the other competing methods by a significant margin.

Clustered Multitask Nonnegative Matrix Factorization for Spectral Unmixing of Hyperspectral Data

In this paper, the new algorithm based on clustered multitask network is proposed to solve spectral unmixing problem in hyperspectral imagery. In the proposed algorithm, the clustered network is employed. Each pixel in the hyperspectral image considered as a node in this network. The nodes in the network are clustered using the fuzzy c-means clustering method. Diffusion least mean square strategy has been used to optimize the proposed cost function. To evaluate the proposed method, experiments are conducted on synthetic and real datasets. Simulation results based on spectral angle distance, abundance angle distance and reconstruction error metrics illustrate the advantage of the proposed algorithm compared with other methods.

Sparsity Constrained Distributed Unmixing of Hyperspectral Data

Spectral unmixing (SU) is a technique to characterize mixed pixels in hyperspectral images measured by remote sensors. Most of the spectral unmixing algorithms are developed using the linear mixing models. To estimate endmembers and fractional abundance matrices in a blind problem, nonnegative matrix factorization (NMF) and its developments are widely used in the SU problem. One of the constraints which was added to NMF is sparsity, that was regularized by Lq norm. In this paper, a new algorithm based on distributed optimization is suggested for spectral unmixing. In the proposed algorithm, a network including single-node clusters is employed. Each pixel in the hyperspectral images is considered as a node in this network. The sparsity constrained distributed unmixing is optimized with diffusion least mean p-power (LMP) strategy, and then the update equations for fractional abundance and signature matrices are obtained. Afterwards the proposed algorithm is analyzed for different values of LMP power and Lq norms. Simulation results based on defined performance metrics illustrate the advantage of the proposed algorithm in spectral unmixing of hyperspectral data compared with other methods.

Hyperspectral Unmixing Based on Clustered Multitask Networks

Hyperspectral remote sensing is a prominent research topic in data processing. Most of the spectral unmixing algorithms are developed by adopting the linear mixing models. Nonnegative matrix factorization (NMF) and its developments are used widely for estimation of signatures and fractional abundances in the SU problem. Sparsity constraints was added to NMF, and was regularized by $ L_ {q} $ norm. In this paper, at first hyperspectral images are clustered by fuzzy c- means method, and then a new algorithm based on sparsity constrained distributed optimization is used for spectral unmixing. In the proposed algorithm, a network including clusters is employed. Each pixel in the hyperspectral images considered as a node in this network. The proposed algorithm is optimized with diffusion LMS strategy, and then the update equations for fractional abundance and signature matrices are obtained. Simulation results based on defined performance metrics illustrate advantage of the proposed algorithm in spectral unmixing of hyperspectral data compared with other methods.

Impulsive Noise Robust Sparse Recovery via Continuous Mixed Norm

This paper investigates the problem of sparse signal recovery in the presence of additive impulsive noise. The heavytailed impulsive noise is well modelled with stable distributions. Since there is no explicit formulation for the probability density function of $S\alpha S$ distribution, alternative approximations like Generalized Gaussian Distribution (GGD) are used which impose $\ell_p$-norm fidelity on the residual error. In this paper, we exploit a Continuous Mixed Norm (CMN) for robust sparse recovery instead of $\ell_p$-norm. We show that in blind conditions, i.e., in case where the parameters of noise distribution are unknown, incorporating CMN can lead to near optimal recovery. We apply Alternating Direction Method of Multipliers (ADMM) for solving the problem induced by utilizing CMN for robust sparse recovery. In this approach, CMN is replaced with a surrogate function and Majorization-Minimization technique is incorporated to solve the problem. Simulation results confirm the efficiency of the proposed method compared to some recent algorithms in the literature for impulsive noise robust sparse recovery.