Primal-Dual Strategy (PDS) for Composite Optimization Over Directed graphs

We investigate the distributed multi-agent sharing optimization problem in a directed graph, with a composite objective function consisting of a smooth function plus a convex (possibly non-smooth) function shared by all agents. While adhering to the network connectivity structure, the goal is to minimize the sum of smooth local functions plus a non-smooth function. The proposed Primal-Dual algorithm (PD) is similar to a previous algorithm \cite{b27}, but it has additional benefits. To begin, we investigate the problem in directed graphs, where agents can only communicate in one direction and the combination matrix is not symmetric. Furthermore, the combination matrix is changing over time, and the condition coefficient weights are produced using an adaptive approach. The strong convexity assumption, adaptive coefficient weights, and a new upper bound on step-sizes are used to demonstrate that linear convergence is possible. New upper bounds on step-sizes are derived under the strong convexity assumption and adaptive coefficient weights that are time-varying in the presence of both smooth and non-smooth terms. Simulation results show the efficacy of the proposed algorithm compared to some other algorithms.

Double-Private Distributed Estimation Algorithm Using Differential Privacy and a Key-Like Proportionate Matrix with Its Performance Analysis

In this brief, we present an enhanced privacy-preserving distributed estimation algorithm, referred to as the ``Double-Private Algorithm," which combines the principles of both differential privacy (DP) and cryptography. The proposed algorithm enhances privacy by introducing DP noise into the intermediate estimations of neighboring nodes. Additionally, we employ an inverse of a closed-form reproducible proportionate gain matrix as the cryptographic key matrix to fortify the privacy protection within the proposed double private algorithm. \textcolor{blue}{We improve the algorithm by transmitting alternative variable vectors instead of raw measurements, resulting in enhanced key matrix reconstruction performance. This innovative approach mitigate noise impact, enhancing overall algorithm effectiveness.} We also establish an upper bound for the norm of the error between the non-private Diffusion Least Mean Square (DLMS) algorithm and our double private algorithm. Further, we determine a sufficient condition for the step-size to ensure the mean convergence of the proposed algorithm. Simulation results demonstrate the effectiveness of the proposed algorithm, particularly its ability to attain the final Mean Square Deviation (MSD) comparable to that of the non-private DLMS.

Second-Order Nonlinearity Estimated and Compensated Diffusion LMS Algorithm: Theoretical Upper Bound, Cramer-Rao Lower bound, and Convergence Analysis

In this paper, an algorithm for estimation and compensation of second-order nonlinearity in wireless sensor setwork (WSN) in distributed estimation framework is proposed. First, the effect of second-order nonlinearity on the performance of Diffusion Least Mean Square (DLMS) algorithm is investigated and an upper bound for $l^2$-norm of the error due to nonlinearity is derived mathematically. Second, mean convergence analysis of the DLMS algorithm in presence of second-order nonlinearity is derived. Third, a distributed algorithm is suggested which consists of extra nonlinearity estimation and compensation units. Moreover, considering the second-order nonlinearity, the Cramer-Rao bound (CRB) for estimating both the unknown vector and nonlinearity coefficient vector is calculated, in which the Fisher information matrix is obtained in a closed-form formula. Simulation results demonstrate the effectiveness of the proposed algorithm in improving the performance of distributed estimation in the presence of nonlinear sensors in a WSN.

Markovian Block Sparse Signal Detection Using One Bit Measurements

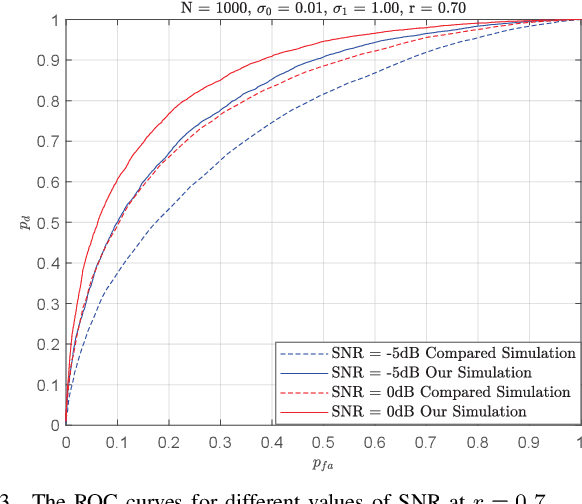
This paper presents a novel sparse signal detection scheme designed for a correlated Markovian Bernoulli-Gaussian sparse signal model, which can equivalently be viewed as a block sparse signal model. Despite the inherent complexity of the model, our approach yields a closed-form detection criterion. Theoretical analyses of the proposed detector are provided, including the computation of false alarm probability and detection probability through closed-form formulas. Simulation results compellingly demonstrate the advantages of our proposed detector compared to an existing detector in the literature.

Diffusion LMS for Distributed Estimation over Wireless Networks with Inter-Node Interference Perturbation

In this paper, we investigate the diffusion least mean square (DLMS) algorithm over fading channel, where in addition to channel noise and path-loss the inter-node-interference (INI) among neighboring nodes of a host node is also taken into account. We also analyze the mean-square convergence behavior of DLMS algorithm, under such condition. In addition, based on an upper bound of the derived network MSD, an optimization problem is defined to find an optimal combination strategy. Furthermore, the adaptive version of the proposed combination strategy is presented. Simulation results corroborate the theoretical findings and indicate the superiority of the proposed combination methods over some previously reported algorithms.

Proportionate Adaptive Graph Signal Recovery

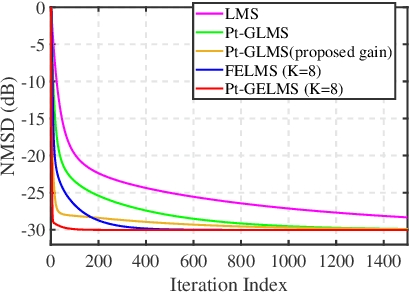
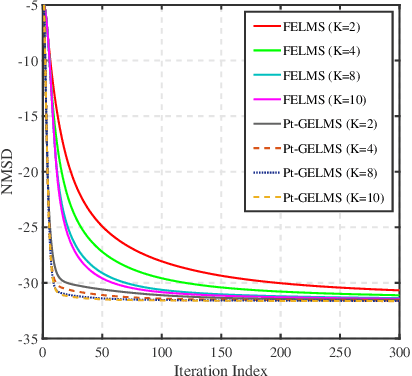
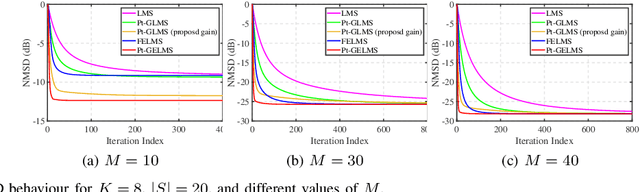
This paper generalizes the proportionate-type adaptive algorithm to the graph signal processing and proposes two proportionate-type adaptive graph signal recovery algorithms. The gain matrix of the proportionate algorithm leads to faster convergence than least mean squares (LMS) algorithm. In this paper, the gain matrix is obtained in a closed-form by minimizing the gradient of the mean-square deviation (GMSD). The first algorithm is the Proportionate-type Graph LMS (Pt-GLMS) algorithm which simply uses a gain matrix in the recursion process of the LMS algorithm and accelerates the convergence of the Pt-GLMS algorithm compared to the LMS algorithm. The second algorithm is the Proportionate-type Graph Extended LMS (Pt-GELMS) algorithm, which uses the previous signal vectors alongside the signal of the current iteration. The Pt-GELMS algorithm utilizes two gain matrices to control the effect of the signal of the previous iterations. The stability analyses of the algorithms are also provided. Simulation results demonstrate the efficacy of the two proposed proportionate-type LMS algorithms.

Double-detector for Sparse Signal Detection from One Bit Compressed Sensing Measurements

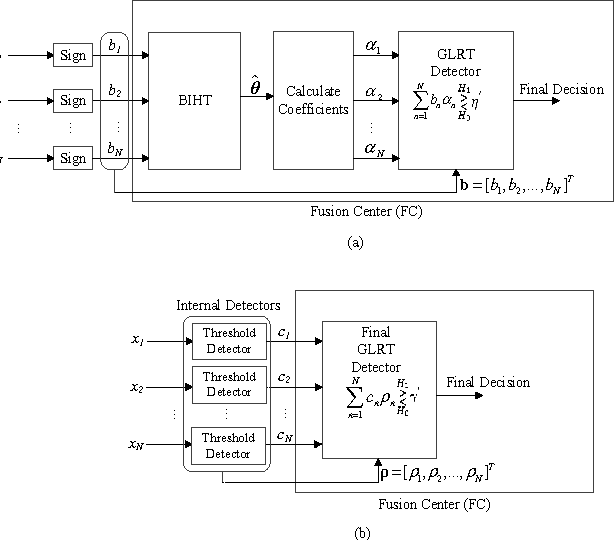
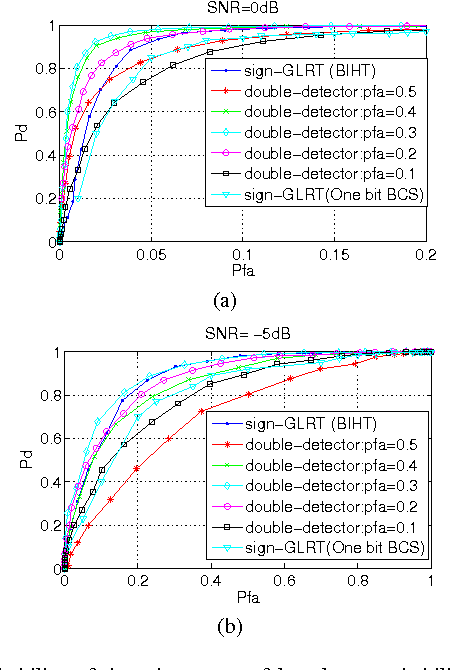
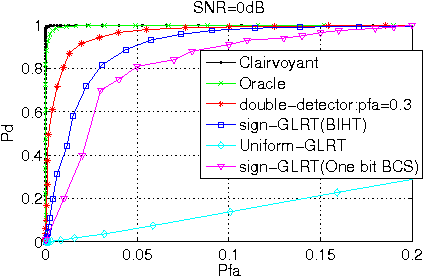
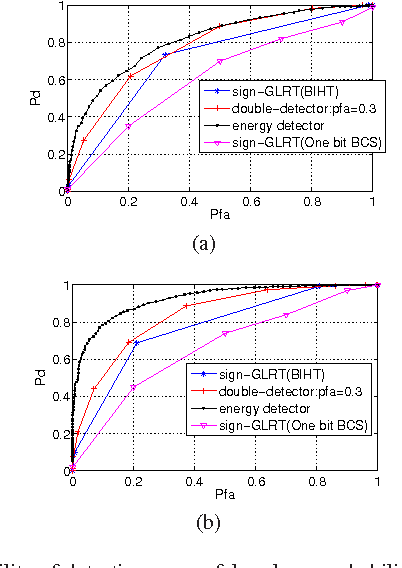
This letter presents the sparse vector signal detection from one bit compressed sensing measurements, in contrast to the previous works which deal with scalar signal detection. In this letter, available results are extended to the vector case and the GLRT detector and the optimal quantizer design are obtained. Also, a double-detector scheme is introduced in which a sensor level threshold detector is integrated into network level GLRT to improve the performance. The detection criteria of oracle and clairvoyant detectors are also derived. Simulation results show that with careful design of the threshold detector, the overall detection performance of double-detector scheme would be better than the sign-GLRT proposed in [1] and close to oracle and clairvoyant detectors. Also, the proposed detector is applied to spectrum sensing and the results are near the well known energy detector which uses the real valued data while the proposed detector only uses the sign of the data.

Sparse Diffusion Steepest-Descent for One Bit Compressed Sensing in Wireless Sensor Networks

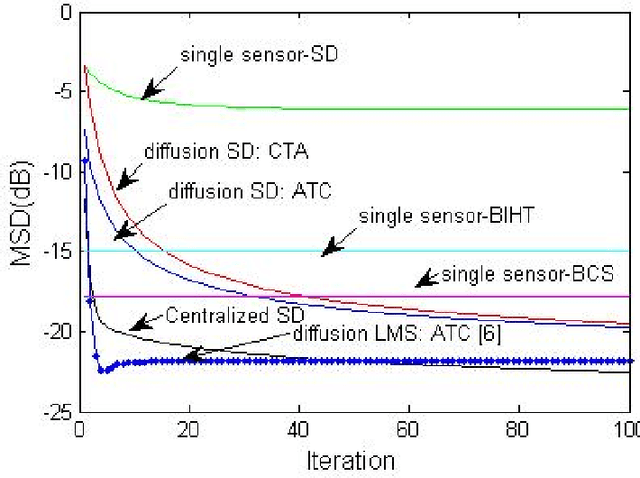
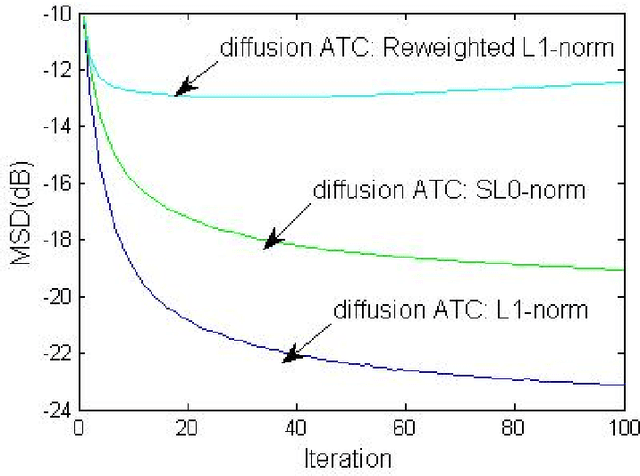
This letter proposes a sparse diffusion steepest-descent algorithm for one bit compressed sensing in wireless sensor networks. The approach exploits the diffusion strategy from distributed learning in the one bit compressed sensing framework. To estimate a common sparse vector cooperatively from only the sign of measurements, steepest-descent is used to minimize the suitable global and local convex cost functions. A diffusion strategy is suggested for distributive learning of the sparse vector. Simulation results show the effectiveness of the proposed distributed algorithm compared to the state-of-the-art non distributive algorithms in the one bit compressed sensing framework.

Dictionary Learning for Blind One Bit Compressed Sensing

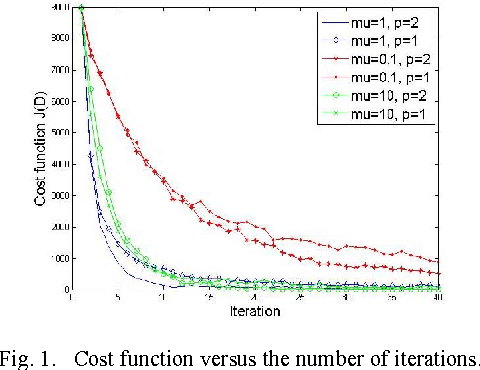
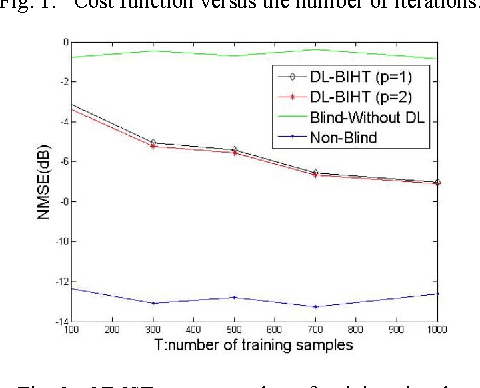
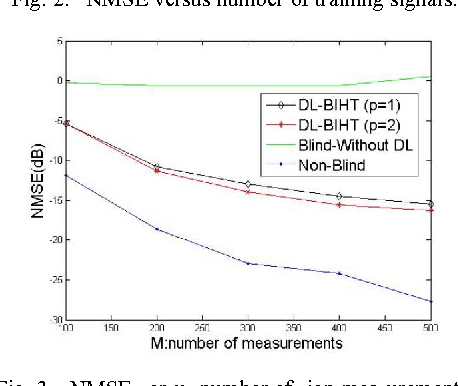
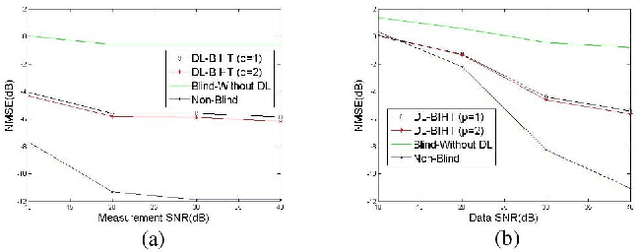
This letter proposes a dictionary learning algorithm for blind one bit compressed sensing. In the blind one bit compressed sensing framework, the original signal to be reconstructed from one bit linear random measurements is sparse in an unknown domain. In this context, the multiplication of measurement matrix $\Ab$ and sparse domain matrix $\Phi$, \ie $\Db=\Ab\Phi$, should be learned. Hence, we use dictionary learning to train this matrix. Towards that end, an appropriate continuous convex cost function is suggested for one bit compressed sensing and a simple steepest-descent method is exploited to learn the rows of the matrix $\Db$. Experimental results show the effectiveness of the proposed algorithm against the case of no dictionary learning, specially with increasing the number of training signals and the number of sign measurements.

Bayesian Hypothesis Testing for Block Sparse Signal Recovery

This letter presents a novel Block Bayesian Hypothesis Testing Algorithm (Block-BHTA) for reconstructing block sparse signals with unknown block structures. The Block-BHTA comprises the detection and recovery of the supports, and the estimation of the amplitudes of the block sparse signal. The support detection and recovery is performed using a Bayesian hypothesis testing. Then, based on the detected and reconstructed supports, the nonzero amplitudes are estimated by linear MMSE. The effectiveness of Block-BHTA is demonstrated by numerical experiments.