Impulsive Noise Robust Sparse Recovery via Continuous Mixed Norm

This paper investigates the problem of sparse signal recovery in the presence of additive impulsive noise. The heavytailed impulsive noise is well modelled with stable distributions. Since there is no explicit formulation for the probability density function of $S\alpha S$ distribution, alternative approximations like Generalized Gaussian Distribution (GGD) are used which impose $\ell_p$-norm fidelity on the residual error. In this paper, we exploit a Continuous Mixed Norm (CMN) for robust sparse recovery instead of $\ell_p$-norm. We show that in blind conditions, i.e., in case where the parameters of noise distribution are unknown, incorporating CMN can lead to near optimal recovery. We apply Alternating Direction Method of Multipliers (ADMM) for solving the problem induced by utilizing CMN for robust sparse recovery. In this approach, CMN is replaced with a surrogate function and Majorization-Minimization technique is incorporated to solve the problem. Simulation results confirm the efficiency of the proposed method compared to some recent algorithms in the literature for impulsive noise robust sparse recovery.

Sparse Diffusion Steepest-Descent for One Bit Compressed Sensing in Wireless Sensor Networks

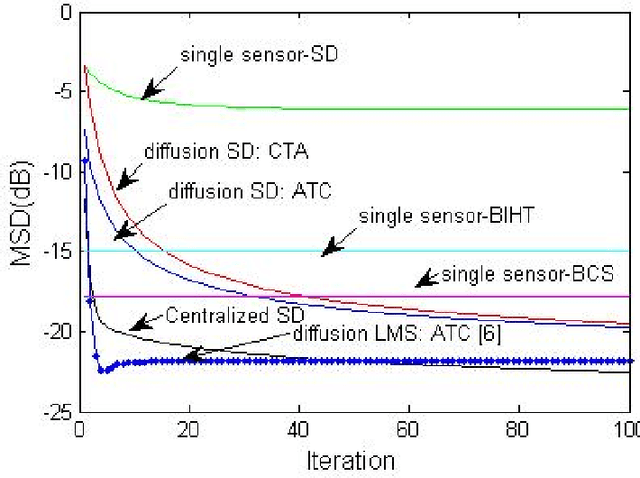
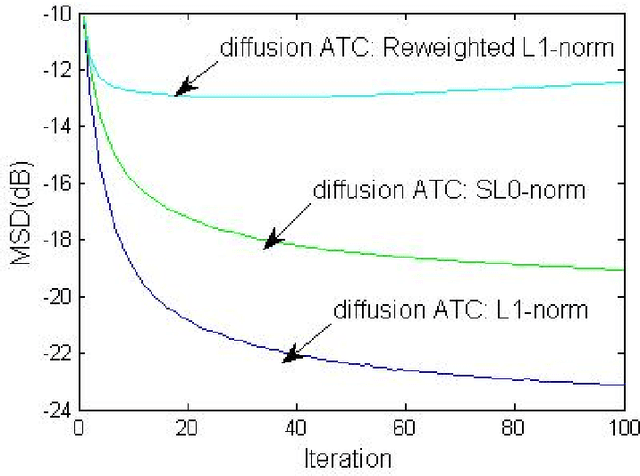
This letter proposes a sparse diffusion steepest-descent algorithm for one bit compressed sensing in wireless sensor networks. The approach exploits the diffusion strategy from distributed learning in the one bit compressed sensing framework. To estimate a common sparse vector cooperatively from only the sign of measurements, steepest-descent is used to minimize the suitable global and local convex cost functions. A diffusion strategy is suggested for distributive learning of the sparse vector. Simulation results show the effectiveness of the proposed distributed algorithm compared to the state-of-the-art non distributive algorithms in the one bit compressed sensing framework.

Dictionary Learning for Blind One Bit Compressed Sensing

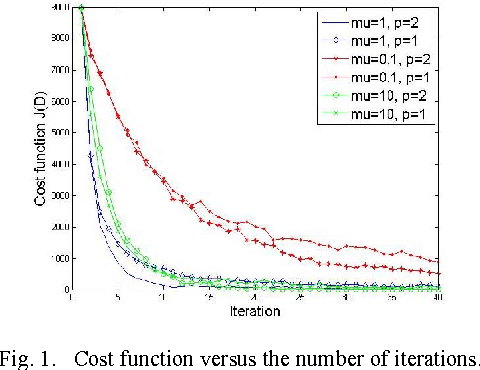
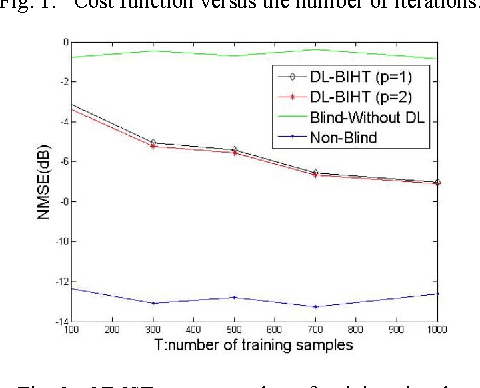
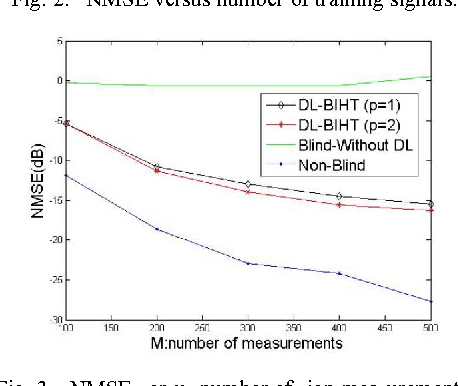
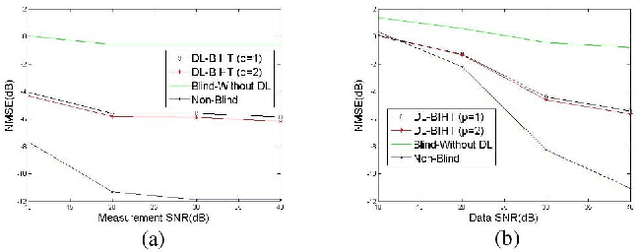
This letter proposes a dictionary learning algorithm for blind one bit compressed sensing. In the blind one bit compressed sensing framework, the original signal to be reconstructed from one bit linear random measurements is sparse in an unknown domain. In this context, the multiplication of measurement matrix $\Ab$ and sparse domain matrix $\Phi$, \ie $\Db=\Ab\Phi$, should be learned. Hence, we use dictionary learning to train this matrix. Towards that end, an appropriate continuous convex cost function is suggested for one bit compressed sensing and a simple steepest-descent method is exploited to learn the rows of the matrix $\Db$. Experimental results show the effectiveness of the proposed algorithm against the case of no dictionary learning, specially with increasing the number of training signals and the number of sign measurements.