Dictionary Learning for Blind One Bit Compressed Sensing
Paper and Code
Aug 30, 2015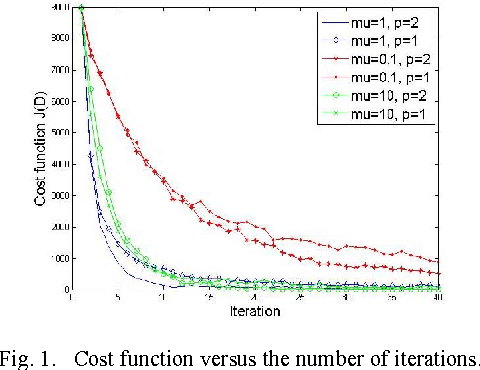
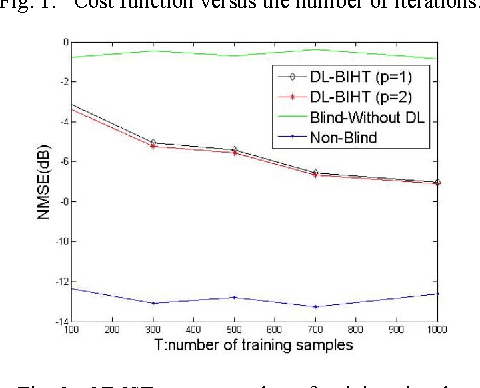
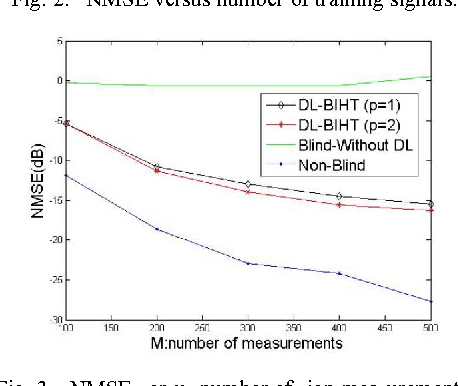
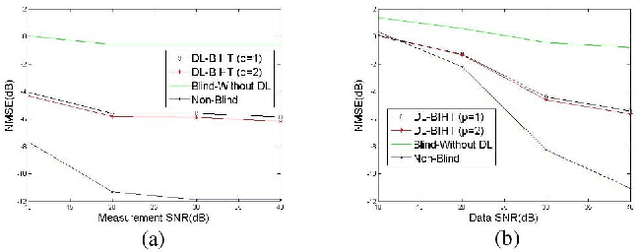
This letter proposes a dictionary learning algorithm for blind one bit compressed sensing. In the blind one bit compressed sensing framework, the original signal to be reconstructed from one bit linear random measurements is sparse in an unknown domain. In this context, the multiplication of measurement matrix $\Ab$ and sparse domain matrix $\Phi$, \ie $\Db=\Ab\Phi$, should be learned. Hence, we use dictionary learning to train this matrix. Towards that end, an appropriate continuous convex cost function is suggested for one bit compressed sensing and a simple steepest-descent method is exploited to learn the rows of the matrix $\Db$. Experimental results show the effectiveness of the proposed algorithm against the case of no dictionary learning, specially with increasing the number of training signals and the number of sign measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge