2DMamba: Efficient State Space Model for Image Representation with Applications on Giga-Pixel Whole Slide Image Classification

Efficiently modeling large 2D contexts is essential for various fields including Giga-Pixel Whole Slide Imaging (WSI) and remote sensing. Transformer-based models offer high parallelism but face challenges due to their quadratic complexity for handling long sequences. Recently, Mamba introduced a selective State Space Model (SSM) with linear complexity and high parallelism, enabling effective and efficient modeling of wide context in 1D sequences. However, extending Mamba to vision tasks, which inherently involve 2D structures, results in spatial discrepancies due to the limitations of 1D sequence processing. On the other hand, current 2D SSMs inherently model 2D structures but they suffer from prohibitively slow computation due to the lack of efficient parallel algorithms. In this work, we propose 2DMamba, a novel 2D selective SSM framework that incorporates the 2D spatial structure of images into Mamba, with a highly optimized hardware-aware operator, adopting both spatial continuity and computational efficiency. We validate the versatility of our approach on both WSIs and natural images. Extensive experiments on 10 public datasets for WSI classification and survival analysis show that 2DMamba~improves up to $2.48\%$ in AUC, $3.11\%$ in F1 score, $2.47\%$ in accuracy and $5.52\%$ in C-index. Additionally, integrating our method with VMamba for natural imaging yields $0.5$ to $0.7$ improvements in mIoU on the ADE20k semantic segmentation dataset, and $0.2\%$ accuracy improvement on ImageNet-1K classification dataset. Our code is available at https://github.com/AtlasAnalyticsLab/2DMamba.

UGrid: An Efficient-And-Rigorous Neural Multigrid Solver for Linear PDEs

Numerical solvers of Partial Differential Equations (PDEs) are of fundamental significance to science and engineering. To date, the historical reliance on legacy techniques has circumscribed possible integration of big data knowledge and exhibits sub-optimal efficiency for certain PDE formulations, while data-driven neural methods typically lack mathematical guarantee of convergence and correctness. This paper articulates a mathematically rigorous neural solver for linear PDEs. The proposed UGrid solver, built upon the principled integration of U-Net and MultiGrid, manifests a mathematically rigorous proof of both convergence and correctness, and showcases high numerical accuracy, as well as strong generalization power to various input geometry/values and multiple PDE formulations. In addition, we devise a new residual loss metric, which enables unsupervised training and affords more stability and a larger solution space over the legacy losses.

Network Topology Inference with Sparsity and Laplacian Constraints

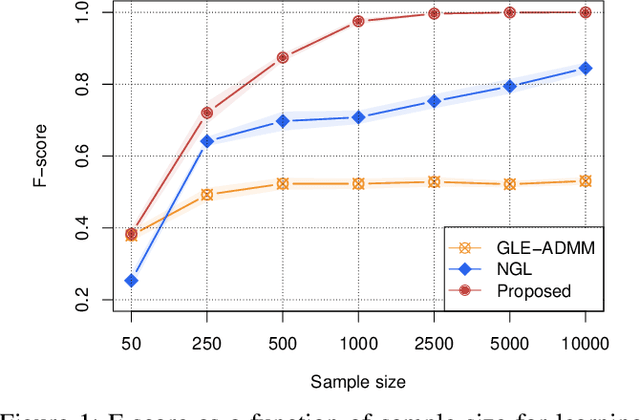
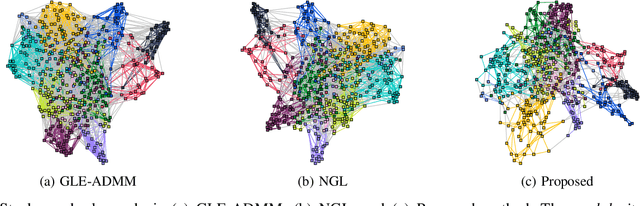
We tackle the network topology inference problem by utilizing Laplacian constrained Gaussian graphical models, which recast the task as estimating a precision matrix in the form of a graph Laplacian. Recent research \cite{ying2020nonconvex} has uncovered the limitations of the widely used $\ell_1$-norm in learning sparse graphs under this model: empirically, the number of nonzero entries in the solution grows with the regularization parameter of the $\ell_1$-norm; theoretically, a large regularization parameter leads to a fully connected (densest) graph. To overcome these challenges, we propose a graph Laplacian estimation method incorporating the $\ell_0$-norm constraint. An efficient gradient projection algorithm is developed to solve the resulting optimization problem, characterized by sparsity and Laplacian constraints. Through numerical experiments with synthetic and financial time-series datasets, we demonstrate the effectiveness of the proposed method in network topology inference.