Xiwen Wang
Mesoscopic Insights: Orchestrating Multi-scale & Hybrid Architecture for Image Manipulation Localization
Dec 18, 2024



Abstract:The mesoscopic level serves as a bridge between the macroscopic and microscopic worlds, addressing gaps overlooked by both. Image manipulation localization (IML), a crucial technique to pursue truth from fake images, has long relied on low-level (microscopic-level) traces. However, in practice, most tampering aims to deceive the audience by altering image semantics. As a result, manipulation commonly occurs at the object level (macroscopic level), which is equally important as microscopic traces. Therefore, integrating these two levels into the mesoscopic level presents a new perspective for IML research. Inspired by this, our paper explores how to simultaneously construct mesoscopic representations of micro and macro information for IML and introduces the Mesorch architecture to orchestrate both. Specifically, this architecture i) combines Transformers and CNNs in parallel, with Transformers extracting macro information and CNNs capturing micro details, and ii) explores across different scales, assessing micro and macro information seamlessly. Additionally, based on the Mesorch architecture, the paper introduces two baseline models aimed at solving IML tasks through mesoscopic representation. Extensive experiments across four datasets have demonstrated that our models surpass the current state-of-the-art in terms of performance, computational complexity, and robustness.
Saliency Guided Optimization of Diffusion Latents
Oct 14, 2024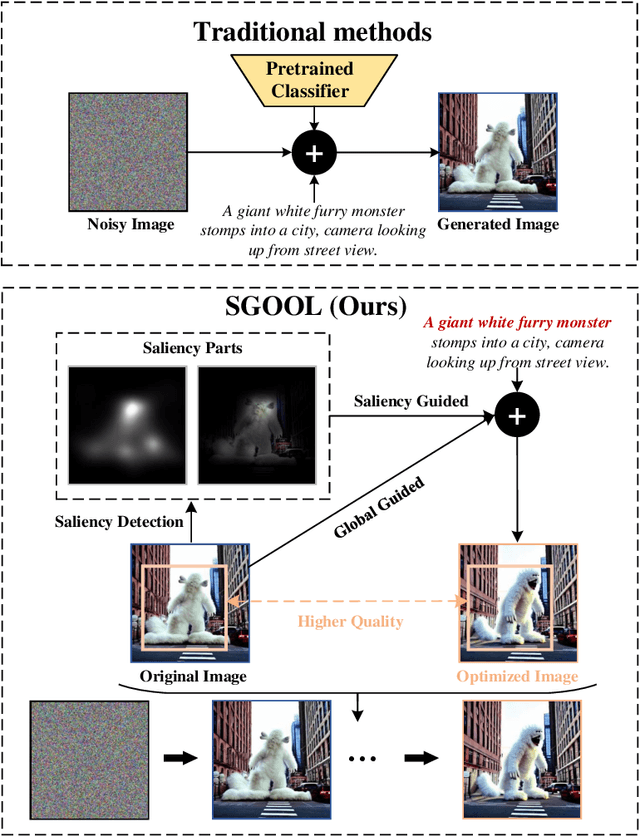

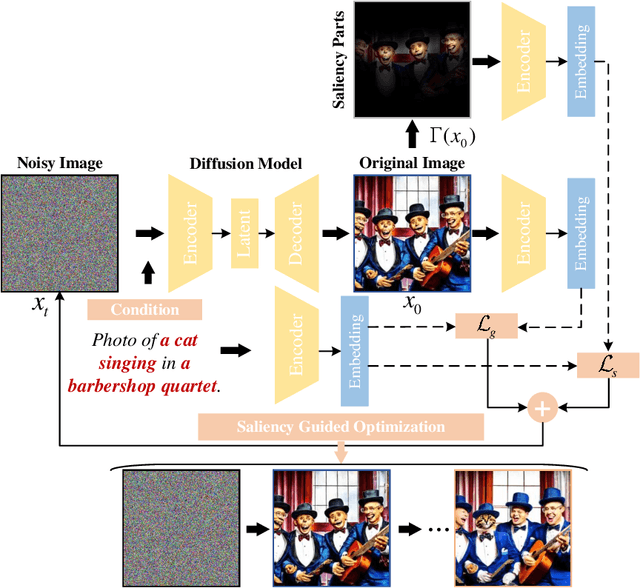
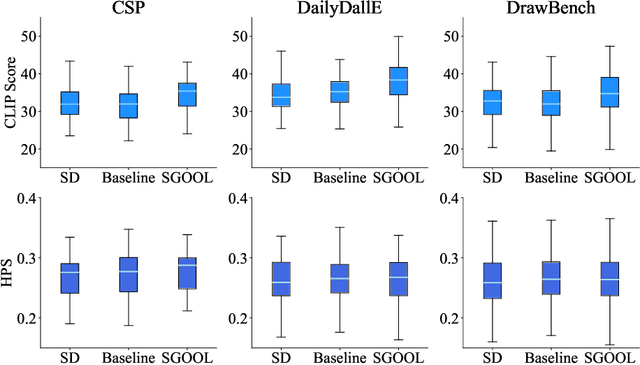
Abstract:With the rapid advances in diffusion models, generating decent images from text prompts is no longer challenging. The key to text-to-image generation is how to optimize the results of a text-to-image generation model so that they can be better aligned with human intentions or prompts. Existing optimization methods commonly treat the entire image uniformly and conduct global optimization. These methods overlook the fact that when viewing an image, the human visual system naturally prioritizes attention toward salient areas, often neglecting less or non-salient regions. That is, humans are likely to neglect optimizations in non-salient areas. Consequently, although model retaining is conducted under the guidance of additional large and multimodality models, existing methods, which perform uniform optimizations, yield sub-optimal results. To address this alignment challenge effectively and efficiently, we propose Saliency Guided Optimization Of Diffusion Latents (SGOOL). We first employ a saliency detector to mimic the human visual attention system and mark out the salient regions. To avoid retraining an additional model, our method directly optimizes the diffusion latents. Besides, SGOOL utilizes an invertible diffusion process and endows it with the merits of constant memory implementation. Hence, our method becomes a parameter-efficient and plug-and-play fine-tuning method. Extensive experiments have been done with several metrics and human evaluation. Experimental results demonstrate the superiority of SGOOL in image quality and prompt alignment.
Learning Large-Scale MTP$_2$ Gaussian Graphical Models via Bridge-Block Decomposition
Sep 29, 2023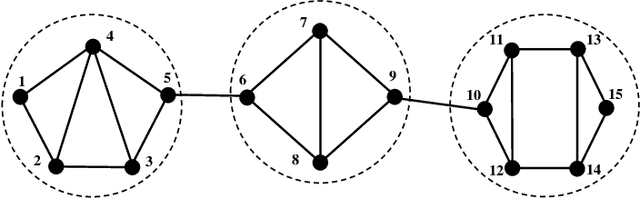

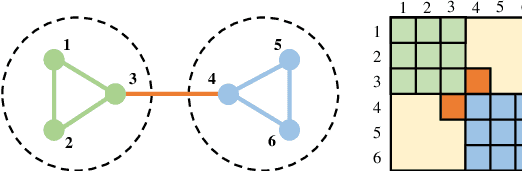
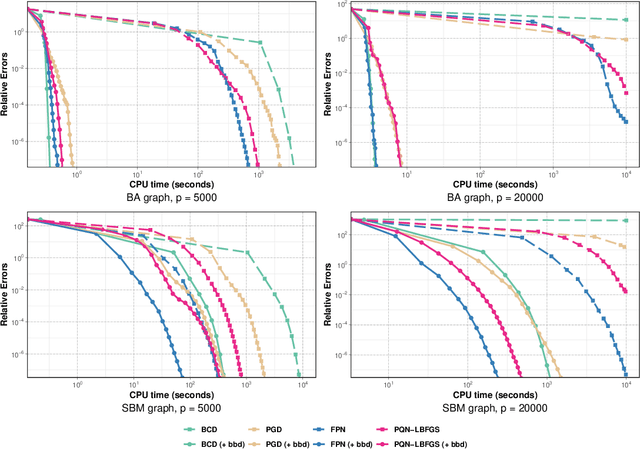
Abstract:This paper studies the problem of learning the large-scale Gaussian graphical models that are multivariate totally positive of order two ($\text{MTP}_2$). By introducing the concept of bridge, which commonly exists in large-scale sparse graphs, we show that the entire problem can be equivalently optimized through (1) several smaller-scaled sub-problems induced by a \emph{bridge-block decomposition} on the thresholded sample covariance graph and (2) a set of explicit solutions on entries corresponding to bridges. From practical aspect, this simple and provable discipline can be applied to break down a large problem into small tractable ones, leading to enormous reduction on the computational complexity and substantial improvements for all existing algorithms. The synthetic and real-world experiments demonstrate that our proposed method presents a significant speed-up compared to the state-of-the-art benchmarks.
Network Topology Inference with Sparsity and Laplacian Constraints
Sep 02, 2023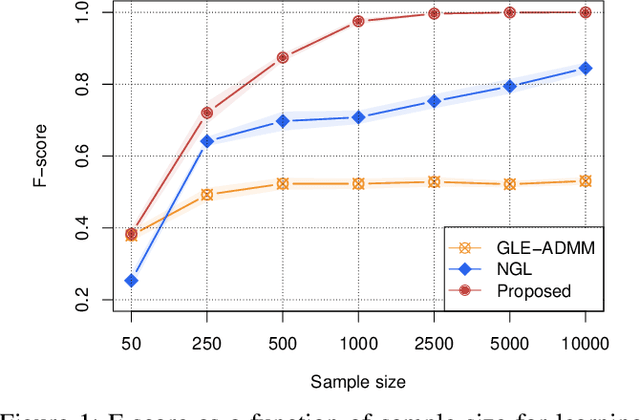
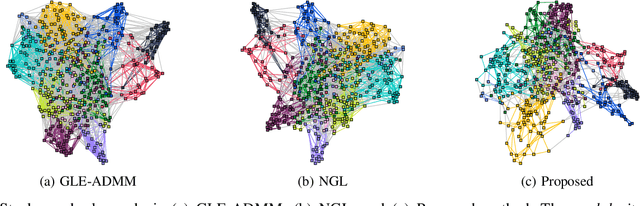
Abstract:We tackle the network topology inference problem by utilizing Laplacian constrained Gaussian graphical models, which recast the task as estimating a precision matrix in the form of a graph Laplacian. Recent research \cite{ying2020nonconvex} has uncovered the limitations of the widely used $\ell_1$-norm in learning sparse graphs under this model: empirically, the number of nonzero entries in the solution grows with the regularization parameter of the $\ell_1$-norm; theoretically, a large regularization parameter leads to a fully connected (densest) graph. To overcome these challenges, we propose a graph Laplacian estimation method incorporating the $\ell_0$-norm constraint. An efficient gradient projection algorithm is developed to solve the resulting optimization problem, characterized by sparsity and Laplacian constraints. Through numerical experiments with synthetic and financial time-series datasets, we demonstrate the effectiveness of the proposed method in network topology inference.
A Fast Successive QP Algorithm for General Mean-Variance Portfolio Optimization
Dec 14, 2022Abstract:The mean and variance of portfolio returns are the standard quantities to measure the expected return and risk of a portfolio. Efficient portfolios that provide optimal trade-offs between mean and variance warrant consideration. To express a preference among these efficient portfolios, investors have put forward many mean-variance portfolio (MVP) formulations which date back to the classical Markowitz portfolio. However, most existing algorithms are highly specialized to particular formulations and cannot be generalized for broader applications. Therefore, a fast and unified algorithm would be extremely beneficial. In this paper, we first introduce a general MVP problem formulation that can fit most existing cases by exploring their commonalities. Then, we propose a widely applicable and provably convergent successive quadratic programming algorithm (SCQP) for the general formulation. The proposed algorithm can be implemented based on only the QP solvers and thus is computationally efficient. In addition, a fast implementation is considered to accelerate the algorithm. The numerical results show that our proposed algorithm significantly outperforms the state-of-the-art ones in terms of convergence speed and scalability.
Efficient and Scalable High-Order Portfolios Design via Parametric Skew-t Distribution
Jun 06, 2022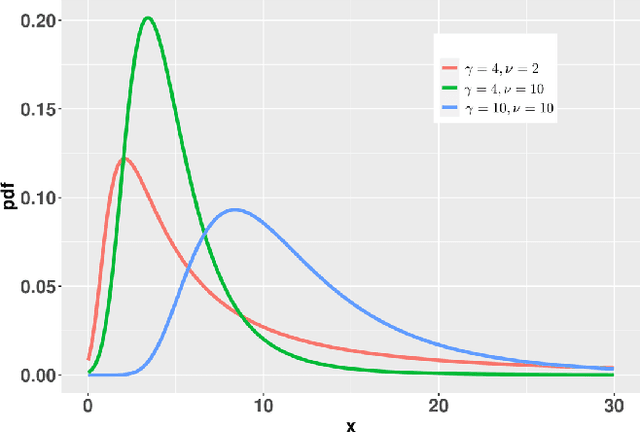
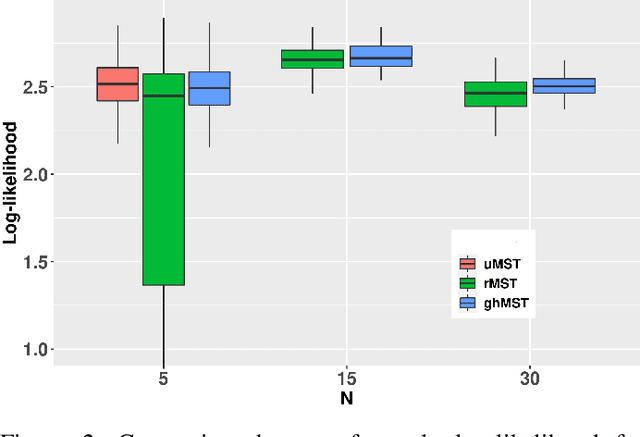
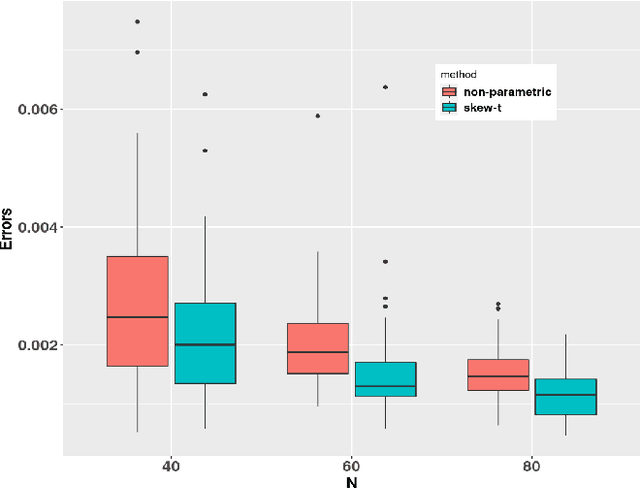
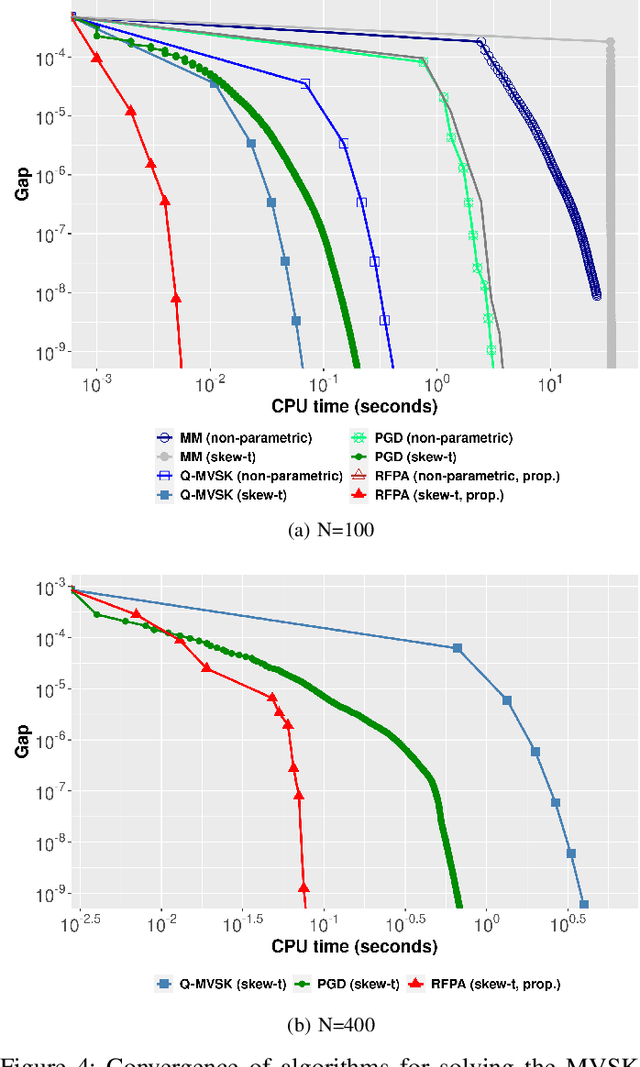
Abstract:Since Markowitz's mean-variance framework, optimizing a portfolio that maximizes the profit and minimizes the risk has been ubiquitous in the financial industry. Initially, profit and risk were measured by the first two moments of the portfolio's return, a.k.a. the mean and variance, which are sufficient to characterize a Gaussian distribution. However, it is broadly believed that the first two moments are not enough to capture the characteristics of the returns' behavior, which have been recognized to be asymmetric and heavy-tailed. Although there is ample evidence that portfolio designs involving the third and fourth moments, i.e., skewness and kurtosis, will outperform the conventional mean-variance framework, they are non-trivial. Specifically, in the classical framework, the memory and computational cost of computing the skewness and kurtosis grow sharply with the number of assets. To alleviate the difficulty in high-dimensional problems, we consider an alternative expression for high-order moments based on parametric representations via a generalized hyperbolic skew-t distribution. Then, we reformulate the high-order portfolio optimization problem as a fixed-point problem and propose a robust fixed-point acceleration algorithm that solves the problem in an efficient and scalable manner. Empirical experiments also demonstrate that our proposed high-order portfolio optimization framework is of low complexity and significantly outperforms the state-of-the-art methods by 2 to 4 orders of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge