Fast Projected Newton-like Method for Precision Matrix Estimation with Nonnegative Partial Correlations
Paper and Code
Dec 12, 2021
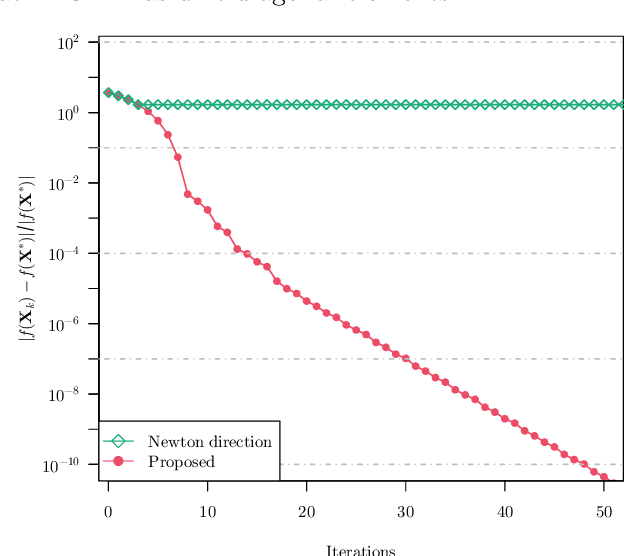
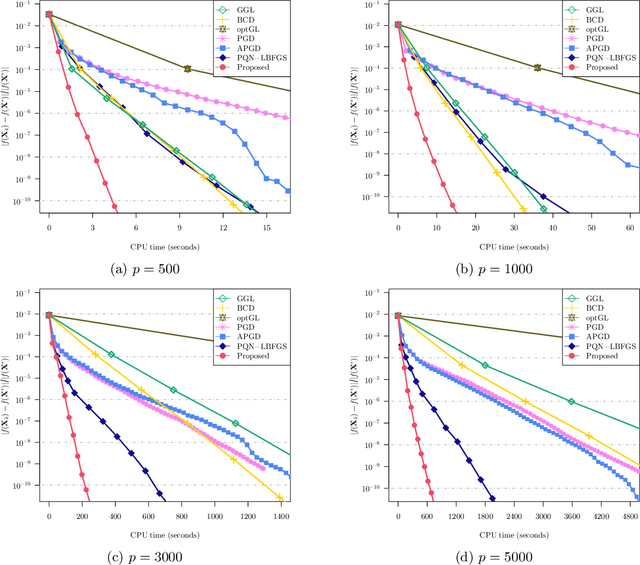
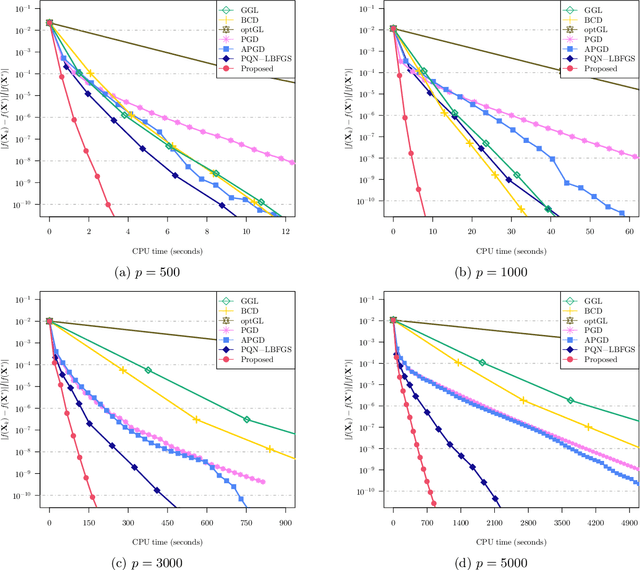
We study the problem of estimating precision matrices in multivariate Gaussian distributions where all partial correlations are nonnegative, also known as multivariate totally positive of order two ($\mathrm{MTP}_2$). Such models have received significant attention in recent years, primarily due to interesting properties, e.g., the maximum likelihood estimator exists with as few as two observations regardless of the underlying dimension. We formulate this problem as a weighted $\ell_1$-norm regularized Gaussian maximum likelihood estimation under $\mathrm{MTP}_2$ constraints. On this direction, we propose a novel projected Newton-like algorithm that incorporates a well-designed approximate Newton direction, which results in our algorithm having the same orders of computation and memory costs as those of first-order methods. We prove that the proposed projected Newton-like algorithm converges to the minimizer of the problem. We further show, both theoretically and experimentally, that the minimizer of our formulation using the weighted $\ell_1$-norm is able to recover the support of the underlying precision matrix correctly without requiring the incoherence condition present in $\ell_1$-norm based methods. Experiments involving synthetic and real-world data demonstrate that our proposed algorithm is significantly more efficient, from a computational time perspective, than the state-of-the-art methods. Finally, we apply our method in financial time-series data, which are well-known for displaying positive dependencies, where we observe a significant performance in terms of modularity value on the learned financial networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge